Abstract
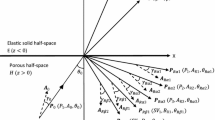
The propagation of elastic waves is studied in a porous solid saturated with two immiscible viscous fluids. The propagation of three longitudinal waves is represented through three scalar potential functions. The lone transverse wave is presented by a vector potential function. The displacements of particles in different phases of the aggregate are defined in terms of these potential functions. It is shown that there exist three longitudinal waves and one transverse wave. The phenomena of reflection and refraction due to longitudinal and transverse waves at a plane interface between an elastic solid half-space and a porous solid half-space saturated with two immiscible viscous fluids are investigated. For the presence of viscosity in pore-fluids, the waves refracted to the porous medium attenuate in the direction normal to the interface. The ratios of the amplitudes of the reflected and refracted waves to that of the incident wave are calculated as a nonsingular system of linear algebraic equations. These amplitude ratios are used to further calculate the shares of different scattered waves in the energy of the incident wave. The modulus of the amplitude and the energy ratios with the angle of incidence are computed for a particular numerical model. The conservation of the energy across the interface is verified. The effects of variations in non-wet saturation of pores and frequencies on the energy partition are depicted graphically and discussed.
Similar content being viewed by others
References
Biot, M. A. General solutions of the equations of elasticity and consolidation for a porous material. Journal of Applied Mechanics, 23, 91–95 (1956)
Biot, M. A. The theory of propagation of elastic waves in a fluid-saturated porous solid, I. lowfrequency range. Journal of the Acoustical Society of America, 28, 168–178 (1956)
Biot, M. A. The theory of propagation of elastic waves in a fluid-saturated porous solid, II. higher frequency range. Journal of the Acoustical Society of America, 28, 179–191 (1956)
Biot, M. A. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 33, 1482–1498 (1962)
Biot, M. A. Generalized theory of acoustic propagation in porous dissipative media. Journal of the Acoustical Society of America, 34, 1254–1264 (1962)
Plona, T. J. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Applied Physics Letters, 36, 259–261 (1980)
Berryman, J. G. Elastic wave propagation in fluid saturated porous media. Journal of the Acoustical Society of America, 69, 416–424 (1981)
Fu, B. J., Li, Z. K., and Wang, S. J. Frontiers of Rock Mechanics and Sustainable Development in the 21st Century, Taylor and Francis, Netherlands (2001)
Denneman, A. I. M., Drijkoningen, G. G., Smeulders, D. M. J., and Wapenaar, K. Reflection and transmission of waves at a fluid/porous-medium interface. Geophysics, 67, 282–291 (2002)
Wei, Z., Wang, Y. S., and Zhang, Z. M. Reflection and transmission of elastic waves propagating from a single-phase elastic medium to a transversely isotropic liquid-saturated porous medium. Acta Mechanica Solida Sinica, 23(2), 183–189 (2002)
Gurevich, B., Ciz, R., and Denneman, A. I. M. Simple expressions for normal incidence reflection coefficients from an interface between fluid-saturated porous materials. Geophysics, 69(6), 1372–1377 (2004)
Lin, C. H., Lee, V. W., and Trifunac, M. D. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid. Soil Dynamics and Earthquake Engineering, 25, 205–223 (2005)
Dai, Z. J., Kuang, Z. B., and Zhao, S. X. Reflection and transmission of elastic waves from the interface of a fluid-saturated porous solid and a double porosity solid. Transport in Porous Media, 65, 237–264 (2006)
Carcione, J. M. Wave Field in Real Media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnatic Media, Elsevier, Amsterdam (2007)
Brutsaert, W. The propagation of elastic waves in unconsolidated unsaturated granular mediums. Journal of Geophysical Research, 69, 243–257 (1964)
Brutsaert, W. and Luthin, J. N. The velocity of sound in soils near the surface as a function of the moistur content. Journal of Geophysical Research, 69(4), 643–652 (1964)
Berryman, J. G., Thigpen, L., and Chin, R. C. Y. Bulk elastic wave propagation in partially saturated porous solids. Journal of the Acoustical Society of America, 84, 360–373 (1988)
Morland, L. W. A simple constitutive theory for a fluid saturated porous solid. Journal of Geophysical Research, 77, 890–900 (1972)
Bedford, A. and Drumheller, D. S. Variational theory of immiscible mixtures. Archive for Rational Mechanics and Analysis, 68, 37–51 (1978)
Bowen, R. M. Incompressible porous media models by use of theory of mixtures. International Journal of Engineering Science, 18, 1129–1148(1980)
Bowen, R. M. Compressible porous media models by use of theory of mixtures. International Journal of Engineering Science, 208, 697–735 (1982)
Hassanizadeh, S. M. and Gray, W. G. Mechanics and thermodynamics of multiphase flow in porous media including interphase boundaries. International Journal of Engineering Science, 13(4), 169–186 (1990)
Bedford, A. and Drumheller, D. S. Theories of immiscible and structured mixtures. International Journal of Engineering Science, 21, 863–960 (1983)
Santos, J. E., Corbero, J., and Douglas, J. Jr. Static and dynamic behavior of a porous solid saturated by a two phase fluid. Journal of the Acoustical Society of America, 87(4), 1428–1438 (1990)
Santos, J. E., Douglas, J. Jr., Corbero, J., and Lovera, O. M. A model for wave propagation in a porous medium saturated by a two phase fluid. Journal of the Acoustical Society of America, 87, 1439–1448 (1990)
Corapcioglu, M. Y. and Tuncay, K. Propagation of waves in porous media. Advances in Porous Media (ed. Corapcioglu, M. Y.), Elsevier, Amsterdam (1996)
Tuncay, K. and Corapcioglu, M. Y. Wave propagation in poroelastic media saturated by two fluids. Journal of Applied Mechanics, 64, 313–319 (1997)
Schanz, M. D. and Diebels, S. A comparative study of Biot’s theory and the linear theory of porous media for wave propagation problems. Acta Mechanica, 161(3–4), 213–235 (2003)
Hanyga, A. Two-fluid porous flow in a single temperature approximation. International Journal of Engineering Science, 42, 1521–1545 (2004)
Lu, J. F. and Hanyga, A. Linear dynamic model for porous media saturated by two immiscible fluids. International Journal of Solids and Structures, 42(9–10), 2689–2709 (2005)
Lo, W. C., Sposito, G., and Majer, E. Wave propagation through elastic porous media containing two immiscible fluids. Water Resources Research, 41, 1–20 (2005)
Lo, W. C., Sposito, G., and Majer, E. Analytical decoupling of poroelasticity equations for acoustic-wave propagation and attenuation in a porous medium containing two immiscible fluids. Journal of Engineering Mathematics, 64, 219–235 (2009)
Sharma, M. D. and Kumar, M. Reflection of attenuated waves at the surface of a porous solid saturated with two immiscible viscous fluids. Geophysical Journal International, 184, 371–384 (2011)
Tomar, S. K. and Arora, A. Reflection and transmission of elastic waves at an elastic/porous solid saturated by two immiscible fluids. International Journal of Solids and Structures, 43, 1991–2013 (2006)
Garg, S. K. and Nayfeh, A. H. Compressional wave propagation in liquid and/or gas saturated elastic porous media. Journal of Applied Physics, 60, 3045–3055 (1986)
Borcherdt, R. D. Reflection-refraction of general P and type-I S waves in elastic and anelastic solids. Geophysical Journal of Royal Astronomical Society, 70, 621–638 (1982)
Achenbach, J. D. Wave Propagation in Elastic Solids, North-Holland, Amsterdam (1973)
Bullen, K. E. An Introduction to the Theory of Seismology, Cambridge University Press, Cambridge (1963)
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the Council of Scientific and Industrial Research (CSIR) of New Delhi (Nos. 09/105(0169)/2008-EMR-I and 09/105(0185)/2009-EMR-I)
Rights and permissions
About this article
Cite this article
Kumar, M., Saini, R. Reflection and refraction of attenuated waves at boundary of elastic solid and porous solid saturated with two immiscible viscous fluids. Appl. Math. Mech.-Engl. Ed. 33, 797–816 (2012). https://doi.org/10.1007/s10483-012-1587-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-012-1587-6
Key words
- dissipative porous solid
- immiscible viscous fluid
- elastic wave
- propagation
- attenuation
- reflection and refraction coefficients