Abstract
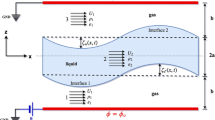
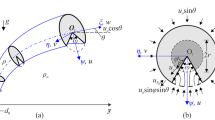
A one-dimensional momentum conservation equation for a straight jet driven by an electrical field is developed. It is presented in terms of a stress component, which can be applied to any constitutive relation of fluids. The only assumption is that the fluid is incompressible. The results indicate that both the axial and radial constitutive relations are required to close the governing equations of the straight charged jet. However, when the trace of the extra stress tensor is zero, only the axial constitutive relation is required. It is also found that the second normal stress difference for the charged jet is always zero. The comparison with other developed momentum equations is made.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Hohman, M. M., Shin, M., Rutledge, G., and Brenner, M. P. Electrospinning and electrically forced jets I: stability theory. Physics of Fluids, 13(8), 2201–2220 (2001)
Feng, J. J. The stretching of an electrified non-Newtonian jet: a model for electrospinning. Physics of Fluids, 14(11), 3912–3926 (2002)
Spivak, A. F. and Dzenis, Y. A. Asymptotic decay of radius of a weakly conductive viscous jet in an external electric field. Applied Physics Letters, 73(21), 3067–3069 (1998)
Yarin, A. L. Free Liquid Jets and Films: Hydrodynamics and Rheology, Longman, New York (1993)
Feng, J. J. Stretching of a straight electrically charged viscoelastic jet. Journal of Non-Newtonian Fluid Mechanics, 116(1), 55–70 (2003)
Reneker, D. H., Yarin, A. L., Fong, H., and Koombhongse, S. Bending instability of electrically charged liquid jets of polymer solutions in electrospinning. Journal of Applied Physics, 87(9), 4531–4547 (2000)
Kowalewski, T., Nski, S., and Barral, S. Experiments and modelling of electrospinning process. Technical Sciences, 53, 385–394 (2005)
Panda, S., Marheineke, N., and Wegener, R. Systematic derivation of an asymptotic model for the dynamics of curved viscous fibers. Mathematical Methods in the Applied Sciences, 31, 1153–1173 (2008)
Zhang, R. J., Liu, Y., Yang, T. T., Hou, S. H., and Chan, C. K. A numerical study of viscosity ratio on instability of electrically driven jets. Mechanics Research Communications, 36(4), 537–545 (2009)
Liu, Y. and Zhang, R. J. Simulation of electrically driven jet using Chebyshev collocation method. Theoretical and Applied Mechanics Letters, 1(3), 031003 (2011)
Ma, H. M. and Zhang, R. J. Axisymmetric stability of electrically forced jets in electrospinning (in Chinese). Chinese Quarterly of Mechanics, 32(4), 480–485 (2011)
Saville, D. A. The Taylor-Melcher leaky dielectric model. Annual Review of Fluid Mechanics, 29, 27–64 (1997)
Lifshitz, E. M., Landau, L. D., and Pitaevskii, L. P. Electrodynamics of Continuous Media, Butterworth-Heinemann, New York (1984)
Byron Bird, R., Armstrong, R. C., and Hassager, O. Dynamics of Polymeric Liquids: Fluid Mechanics, Wiley-InterScience, New York (1987)
Eggers, J. Universal pinching of 3D axisymmetrical free-surface flow. Physical Review Letters, 71(21), 3458–3460 (1993)
Yarin, A. L., Koombhongse, S., and Reneker, D. H. Bending instability in electrospinning of nanofibers. Journal of Applied Physics, 89, 3018–3026 (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (No. 10772136) and the Research Committee of The Hong Kong Polytechnic University (No. G-YE70)
Rights and permissions
About this article
Cite this article
Zhang, Rj., Hou, S.H. & Chan, C.K. Momentum equation for straight electrically charged jet. Appl. Math. Mech.-Engl. Ed. 32, 1515–1524 (2011). https://doi.org/10.1007/s10483-011-1520-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-011-1520-9