Skip to main content
SpringerLink
Log in

Response of loose bonding on reflection and transmission of elastic waves at interface between elastic solid and micropolar porous cubic crystal

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

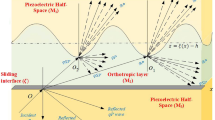
The problem of reflection and transmission of plane periodic waves incident on the interface between the loosely bonded elastic solid and micropolar porous cubic crystal half spaces is investigated. This is done by assuming that the interface behaves like a dislocation, which preserves the continuity of traction while allowing a finite amount of slip. Amplitude ratios of various reflected and transmitted waves have been depicted graphically. Some special cases of interest have been deduced from the present investigation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Nunziato, J. W. and Cowin, S. C. A non-linear theory of elastic materials with voids. Archive Rational Mechanics and Analysis 72(2), 175–201 (1979)

    MATH  MathSciNet  Google Scholar 

  2. Cowin, S. C. and Nunziato, J. W. Linear elastic materials with voids. Journal of Elasticity 13(2), 125–147 (1983)

    Article  MATH  Google Scholar 

  3. Suhubi, E. S. and Eringen, A. C. Non-linear theory of simple microelastic solids II. International Journal of Engineering Science 2(4), 389–404 (1964)

    Article  MathSciNet  Google Scholar 

  4. Eringen, A. C. Microcontinuum Field Theories I: Foundations and Solids, Springer-Verlag, New York (1999)

    Google Scholar 

  5. Mindlin, R. D. Microstructure in linear elasticity. Archive Rational Mechanics and Analysis 16(1), 51–78 (1964)

    MATH  MathSciNet  Google Scholar 

  6. Eringen, A. C. Linear theory of micropolar elasticity. Journal of Mathematics and Mechanics 15(6), 909–923 (1966)

    MATH  MathSciNet  Google Scholar 

  7. Scarpetta, E. On the fundamental solutions in micropolar elasticity with voids. Acta Mechanica 82(3–4), 151–158 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  8. Passarella, F. Some results in micropolar thermoelasticity. Mechanics Research Communications 23(4), 349–357 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  9. Marin, M. Some basic theorems in elastostatics of micropolar materials with voids. Journal of Computational and Applied Mathematics 70(1), 115–126 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  10. Minagawa, S., Arakawa, K., and Yamada, M. Dispersion curves for waves in a cubic micropolar medium with reference to estimations of the material constants for diamond. The Japan Society of Mechanical Engineers 24(187), 22–28 (1981)

    Google Scholar 

  11. Atanackovic, T. M. and Guran, A. Theory of Elasticity for Scientists and Engineers, Birkhäuser, Boston (2000)

    Google Scholar 

  12. Murti, G. S. Reflection, transmission and attenuation of elastic waves at a loosely-bonded interface of two half spaces. Geophysical Journal of the Royal Astronomical Society 44(2), 389–404 (1976)

    Google Scholar 

  13. Eringen, A. C. Plane waves in nonlocal micropolar elasticity. International Journal of Engineering Science 22(8–10), 1113–1121 (1984)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Kurukshetra University, Kurukshetra, 136119, India

    Rajneesh Kumar & Meenakshi Panchal

Authors
  1. Rajneesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Meenakshi Panchal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajneesh Kumar.

Additional information

Communicated by Xing-ming GUO

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kumar, R., Panchal, M. Response of loose bonding on reflection and transmission of elastic waves at interface between elastic solid and micropolar porous cubic crystal. Appl. Math. Mech.-Engl. Ed. 31, 605–616 (2010). https://doi.org/10.1007/s10483-010-0508-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-010-0508-x

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation