Abstract
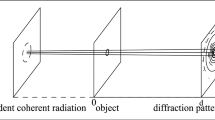
A new algorithm for phase contrast X-ray tomography under holographic measurement was proposed in this paper. The main idea of the algorithm was to solve the nonlinear phase retrieval problem using the Newton iterative method. The linear equations for the Newton directions were proved to be ill-posed and the regularized solutions were obtained by the conjugate gradient method. Some numerical experiments with computer simulated data were presented. The efficiency, feasibility and the numerical stability of the algorithm were illustrated by the numerical experiments. Compared with the results produced by the linearized phase retrieval algorithm, we can see that the new algorithm is not limited to be only efficient for the data measured in the near-field of the Fresnel region and thus it has a broader validity range.
Similar content being viewed by others
References
Lewis R A. Medical phase contrast x-ray imaging: Current status and future prospects[J]. Physics in Medicine and Biology, 2004, 49:3573–3583.
Suzuki Y, Yagi N, Uesugi K. X-ray refraction-enhanced imaging and a method for phase retrieval for a simple object[J]. Journal of Synchrotron Radiation, 2002, 9:160–165.
Spanne P, Raven C, Snigireva I, et al. In-line holography and phase-contrast microtomography with high energy x-rays[J]. Physics in Medicines and Biology, 1999, 44:741–749.
Arfelli F, Assante M, V Bonvicini, et al. Low-dose phase contrast x-ray medical imaging[J]. Physics in Medicine and Biology, 1998, 43:2845–2852.
Ingal V N, Beliaevskaya E A, Brianskaya A P, et al. Phase mammography-a new technique for breast investigation[J]. Physics in Medicine and Biology, 1998, 43:2555–2567.
Ando M, Hosoya S. An attempt at x-ray phase-contrast microscopy[C]. In: Shinoda G, Kohra K, and Ichinokawa T (eds). Proceedings of the 6th International Conference of X Ray Optics and Microanalysis, Tokyo: Univerisity of Tokyo Press, 1972, 63–68.
Momose A. Demonstration of phase-contrast X-ray computed tomography using an X-ray interferometer[J]. Nuclear Instruments and Methods in Physics Research A, 1995, 352:622–628.
Chapman D, Thomlinson W, Johnston R E, et al. Diffraction enhanced x-ray imaging[J]. Physics in Medicine and Biology, 1997, 42:2015–2025.
Dilmanian F A, Zhong Z, Ren B, et al. Computed tomography of x-ray index of refraction using the diffraction enhanced imaging method[J]. Physics in Medicine and Biology, 2000, 45:933–946.
Pfeiffer F, Weitkamp T, Bunk O, et al. Phase retrieval and differential phase-contrast imaging with low-brilliance x-ray sources[J]. Nature Physics, 2006, 2:258–261.
Momose A, Yashiro W, Takeda Y, et al. Phase tomography by x-ray talbot interferometry for biological imaging[J]. Japanese of Applied Physics, 2006, 45(6A):5254–5262.
Gureyev T E, Nugent K A. Rapid quantitative phase imaging using the transport of intensity equation[J]. Optics Communications, 1997, 133:339–346.
Barty A, Nugent K A, Roberts A, et al. Quantitative phase tomography[J]. Optics Communication, 2000, 175:329–336.
Gureyev T E, Raven C, Snigirev A, Snigireva I, Wilkins S W. Hard x-ray quantitative non-interferometric phase-contrast microscopy[J]. Journal of Physics D: Applied Physics, 1999, 32:563–567.
Jonas P, Louis A K. Phase contrast tomography using holographic measurements[J]. Inverse Problems, 2004, 20(1):75–102.
Bronnikov A V. Theory of quantitative phase-contrast computed tomography[J]. Journal of the Optical Society of America A, 2002, 19(3):472–480.
Born M, Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light[M]. Cambridge: Cambridge University Press, 2001.
Gureyev T E, Wilkins S W. On x-ray phase imaging with a point source[J]. Journal of the Optical Society of America A, 1998, 15(3):579–585.
Als-Nielsen J, McMorrow D. Elements of modern X-ray physics[M]. New York: Wiley, 2001.
Wu X, Deans A E, Liu H. X-ray diagnostic techniques[M]. In: T Vo-Dinh (ed). Biomedical Photonics Handbook, Tampa: CRC Press, 2003, 26.1–26.34.
Gureyev T E, Pogany A, Paganin D M, et al. Linear algorithms for phase retrieval in the Fresnel region[J]. Optics Communications, 2004, 231:53–70.
Huntley J M. Noise-immune phase unwrapping algorithm[J]. Applied Optics, 1989, 28(15):3268–3270.
Kak A C, Slaney M. Principles of computerized tomographic imaging[M]. New York: IEEE Press, 1988.
Kaipio J, Somersalo E. Statistical and computational inverse problems[M]. New York: Springer, 2005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by GUO Mao-zheng
Project supported by the National Basic Research Program of China (No. 2003CB716101), the National Natural Science Foundation of China (No. 60532080), the Science Foundation of Chinese Ministry of Education (No. 306017), the Science Foundation of Engineering Research Institute of Peking University, and the Science Foundation of Microsoft Research of Asia.
Rights and permissions
About this article
Cite this article
Ni, Wl., Zhou, T. Algorithm for phase contrast X-ray tomography based on nonlinear phase retrieval. Appl. Math. Mech.-Engl. Ed. 29, 101–112 (2008). https://doi.org/10.1007/s10483-008-0112-8
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s10483-008-0112-8