Skip to main content
SpringerLink
Log in

Global qualitative analysis of new Monod type chemostat model with delayed growth response and pulsed input in polluted environment

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

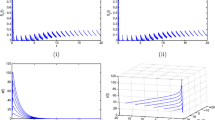
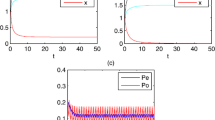
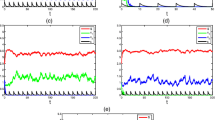
In this paper, we consider a new Monod type chemostat model with time delay and impulsive input concentration of the nutrient in a polluted environment. Using the discrete dynamical system determined by the stroboscopic map, we obtain a “microorganism-extinction” periodic solution. Further, we establish the sufficient conditions for the global attractivity of the microorganism-extinction periodic solution. Using new computational techniques for impulsive and delayed differential equation, we prove that the system is permanent under appropriate conditions. Our results show that time delay is “profitless”.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hsu S B. A competition model for a seasonally fluctuating nutrient[J]. Journal of Mathematical Biology, 1980, 9(2):115–132.

    Article  MATH  MathSciNet  Google Scholar 

  2. Smith H L. Competitive coexistence in an oscillating chemostat[J]. SIAM Journal on Applied Mathematics, 1981, 40(3):498–522.

    Article  MATH  MathSciNet  Google Scholar 

  3. Butler G J, Hsu S B, Waltman P. A mathematical model of the chemostat with periodic washout rate[J]. SIAM Journal on Applied Mathematics, 1985, 45(3):435–449.

    Article  MATH  MathSciNet  Google Scholar 

  4. Pilyugin S S, Waltman P. Competition in the unstirred chemostat with periodic input and washout[J]. SIAM Journal on Applied Mathematics, 1999, 59(4):1157–1177.

    Article  MATH  MathSciNet  Google Scholar 

  5. Simth H L, Waltman P. The theory of the chemostat[M]. Cambridge: Cambridge University Press, 1995.

    Google Scholar 

  6. Hsu S B, Hubbell S P, Waltman P. A mathematical theory for single nutrient competition in continuous cultures of micro-organisms[J]. SIAM Journal on Applied Mathematics, 1977, 32(2):366–382.

    Article  MATH  MathSciNet  Google Scholar 

  7. Picket A M. Growth in a changing environment[M]. In: Bazin M J (ed). Microbial Population Dynamics, Florida: CRC Press, 1982.

    Google Scholar 

  8. Monod J. La technique de culture continue; théorie et applications[J]. Ann Inst Pasteur, 1950, 79(19):390–401.

    Google Scholar 

  9. Hansen S R, Hubbell S P. Single-nutrient microbial competition: qualitative agreement between experimental and theoretically forecast outcomes[J]. Science, 1980, 207(4438):1491–1493.

    Article  Google Scholar 

  10. Barford J P, Pamment N B, Hall R J. Lag phases and transients[M]. In: Bazin M J (ed). Microbial Population Dynamics, Florida: CRC Press, 1982.

    Google Scholar 

  11. Ramkrishna D, Fredrickson A G, Tsuchiya H M. Dynamics of microbial propagation: models considering inhibitors and variable cell composition[J]. Biotechnology and Bioengineering, 1967, 9(2):129–170.

    Article  Google Scholar 

  12. Bush A W, Cook A E. The effect of time delay and growth rate inhibition in the bacterial treatment of wastewater[J]. Journal of Theoretical Biology, 1976, 63(2):385–395.

    Article  Google Scholar 

  13. Caperon J. Time lag in population growth response of isochrysis galbana to a variable nitrate environment[J]. Ecology, 1969, 50(2):188–192.

    Article  Google Scholar 

  14. Freedman H I, So J W-H, Waltman P. Coexistence in a model of competition in the chemostat incorporating discrete delays[J]. SIAM Journal on Applied Mathematics, 1989, 49(3):859–870.

    Article  MATH  MathSciNet  Google Scholar 

  15. Freedman H I, So J W-H, Waltman P. Chemostat competition with time delays[M]. In: Eisenfeld J, Levine D S (eds). Biomedical Modelling and Simulation, New York: Scientific Publishing Co, 1989.

    Google Scholar 

  16. Ruan Shi-gui, Wolkowicz Gail S K. Bifurcation analysis of a chemostat model with a distributed delay[J]. Journal of Mathematical Analysis and Applications, 1996, 204(3)786–812.

    Article  MATH  MathSciNet  Google Scholar 

  17. Thingstad T F, Langeland T I. Dynamics of chemostat culture: the effect of a delay in cell response[J]. Journal of Theoretical Biology, 1974, 48(1):149–159.

    Article  Google Scholar 

  18. Ellermeyer S F. Competition in the chemostat: global asymptotic behavior of a model with delayed response in growth[J]. SIAM Journal on Applied Mathematics, 1994, 54(2):456–465.

    Article  MATH  MathSciNet  Google Scholar 

  19. Wolkowicz Gail S K, Xia H. Global asymptotic behavior of a chemostat model with discrete delays[J]. SIAM Journal on Applied Mathematics, 1997, 57(4):1019–1043.

    Article  MATH  MathSciNet  Google Scholar 

  20. Wolkowicz Gail S K, Xia Hua-xing, Ruan Shi-gui. Competition in the chemostat: a distributed delay model and its global asymptotic behavior[J]. SIAM Journal on Applied Mathematics, 1997, 57(5):1281–1310.

    Article  MATH  MathSciNet  Google Scholar 

  21. Xia Hua-xing, Wolkowicz Gail S K, Wang Lin. Transient oscillations induced by delayed growth response in the chemostat[J]. Journal of Mathematical Biology, 2005, 50(5):489–530.

    Article  MATH  MathSciNet  Google Scholar 

  22. Zhao Tao. Global periodic solutions for a differential delay system modelling a microbial population in the chemostat[J]. Journal of Mathematical Analysis and Applications, 1995, 193(1):329–352.

    Article  MATH  MathSciNet  Google Scholar 

  23. MacDonald N. Time delays in chemostat models[M]. In: Bazin M J (ed). Microbial Population Dynamics, Florida: CRC Press, 1982.

    Google Scholar 

  24. Hale J K, Somolinas A S. Competition for fluctuating nutrient[J]. Journal of Mathematical Biology, 1983, 18(3):255–280.

    Article  MATH  MathSciNet  Google Scholar 

  25. Buler G J, Hsu S B, Waltman P. A mathematical model of the chemostat with periodic washout rate[J]. SIAM Journal on Applied Mathematics, 1985, 45(3):435–449.

    Article  MathSciNet  Google Scholar 

  26. Wolkowicz Gail S K, Zhao Xiao-qiang. N-spicies competition in a periodic chemostat[J]. Differential and Integral Equations: An International Journal for Theory and Applications, 1998, 11(3):465–491.

    MATH  MathSciNet  Google Scholar 

  27. Funasaki E, Kot M. Invasion and chaos in a periodically pulsed mass-action chemostat[J]. Theoretical Population Biology, 1993, 44(2):203–224.

    Article  MATH  Google Scholar 

  28. Smith R J, Wolkowicz Gail S K. Analysis of a model of the nutrient driven self-cycling fermentation process[J]. Dynamics of Continuous, Discrete and Impulsive Systems, Series B, 2004, 11(2):239–265.

    MATH  Google Scholar 

  29. Sun Shu-lin, Chen Lan-sun. Dynamic behaviors of Monod type chemostat model with impulsive perturbation on the nutrient concentration[J]. Journal of Mathematical Chemistry, 2007, 42(4):837–848.

    Article  Google Scholar 

  30. Bainov D, Simeonov P. Impulsive differential eqations: periodic solutions and applications[M]. Harlow: Longman Scientific and Technical Press, 1993.

    Google Scholar 

  31. Lakshmikantham V, Bainov D, Simeonov P. Theory of impulsive differential equations[M]. Singapore: World Scientific, 1989.

    Google Scholar 

  32. Liu Xian-ning, Chen Lan-sun. Complex dynamics of Holling type II Lotka-Volterra predator-prey system with impulsive perturbations on the predator[J]. Chaos, Solitons and Fractals, 2003, 16(2):311–320.

    Article  MATH  MathSciNet  Google Scholar 

  33. Roberts M G, Kao R R. The dynamics of an infectious disease in a population with birth pulses[J]. Mathematical Biosciences, 1998, 149(1):23–36.

    Article  MATH  Google Scholar 

  34. Ballinger G, Liu X. Permanence of population growth models with impulsive effects[J]. Mathematical and Computer Modelling, 1997, 26(12):59–72.

    Article  MathSciNet  Google Scholar 

  35. Sun Ming-jing, Chen Lan-sun. Analysis of the dynamical behavior for enzyme-catalyzed reactions with impulsive input[J]. Journal of Mathematical Chemistry, 2006, DOI: 10.1007/s10910-006-9207-5.

  36. Chen Lan-sun, Chen Jian. Nonlinear biological dynamic systems[M]. Beijing: Science Press, 1993 (in Chinese).

    Google Scholar 

  37. Kuang Yang. Delay differential equations with applications in population dynamics[M]. California: Academic Press Inc, 1993.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, Shandong University of Science and Technology, Qingdao, 266510, Shandong Province, P. R. China

    Meng Xin-zhu  (孟新柱) & Zhao Qiu-lan  (赵秋兰)

  2. Department of Applied Mathematics, Dalian University of Technology, Dalian, 116024, Liaoning Province, P. R. China

    Meng Xin-zhu  (孟新柱) & Chen Lan-sun  (陈兰荪)

  3. Institute of Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing, 100080, P. R. China

    Chen Lan-sun  (陈兰荪)

Authors
  1. Meng Xin-zhu  (孟新柱)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhao Qiu-lan  (赵秋兰)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chen Lan-sun  (陈兰荪)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Meng Xin-zhu  (孟新柱).

Additional information

Communicated by GUO Xing-ming

Project supported by the National Natural Science Foundation of China (Nos. 10471117 and 10771179) and the Natural Science Foundation of Shandong University of Science and Technology (No. 05g016)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Meng, Xz., Zhao, Ql. & Chen, Ls. Global qualitative analysis of new Monod type chemostat model with delayed growth response and pulsed input in polluted environment. Appl. Math. Mech.-Engl. Ed. 29, 75–87 (2008). https://doi.org/10.1007/s10483-008-0110-x

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-008-0110-x

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation