Skip to main content
SpringerLink
Log in

Modal analysis of coupled vibration of belt drive systems

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

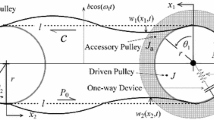
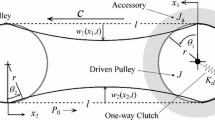
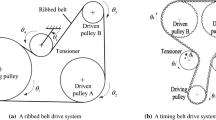
The modal method is applied to analyze coupled vibration of belt drive systems. A belt drive system is a hybrid system consisting of continuous belts modeled as strings as well as discrete pulleys and a tensioner arm. The characteristic equation of the system is derived from the governing equation. Numerical results demenstrate the effects of the transport speed and the initial tension on natural frequencies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen L Q, Zu J W. Advance in analysis of vibrations of serpentine belt drive systems[J]. Mechanics in Engineering, 2001, 23(4):8–12 (in Chinese).

    Google Scholar 

  2. Chen L Q. Analysis and control of transverse vibrations of axially moving strings[J]. ASME Applied Mechanics Reviews, 2005, 58(2):91–116.

    Article  Google Scholar 

  3. Ulsoy A G, Whitesell J E, Hooven M D. Design of belt-tensioner systems for dynamic stability[J]. ASME Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1985, 107(2):282–290.

    Google Scholar 

  4. Beikmann R S, Perkins N C, Ulsoy A G. Free vibration of serpentine belt drive systems[J]. ASME Journal of Vibration and Acoustics, 1996, 118(3):406–413.

    Google Scholar 

  5. Beikmann R S, Perkins N C, Ulsoy A G. Nonlinear coupled response of serpentine belt drive systems[J]. ASME Journal of Vibration and Acoustics, 1996, 118(4):567–574.

    Google Scholar 

  6. Zhang L, Zu J W. Modal analysis of serpentine belt drive systems[J]. Journal of Sound and Vibration, 1999, 222(2):259–279.

    Article  Google Scholar 

  7. Zhang L, Zu J W. One-to-one auto-parametric resonance in serpentine belt drive systems[J]. Journal of Sound and Vibration, 2000, 232(4):783–806.

    Article  MathSciNet  Google Scholar 

  8. Zhang L Zu J W, Hou Z. Complex modal analysis of non-self-adjoint hybrid serpentine belt drive systems[J]. ASME Journal of Vibration and Acoustics, 2001, 123(2):150–156.

    Article  Google Scholar 

  9. Parker R G. Efficient eigensolution, dynamic response, and eigensensitivity of serpentine belt drives[J]. Journal of Sound and Vibration, 2004, 270(1):15–38.

    Article  Google Scholar 

  10. Leamy M J, Wasfy T M. Transient and steady-state dynamic finite element modeling of beltdrives[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2002, 124(6):575–581.

    Article  Google Scholar 

  11. Leamy M J. On a perturbation method for the analysis of unsteady belt-drive operation[J]. ASME Journal of Applied Mechanics, 2005, 72(4):570–580.

    Article  MATH  Google Scholar 

  12. Tonoli A, Amati N, Zenerino E. Dynamic modeling of belt drive systems: effects of the shear deformations[J]. ASME Journal of Vibration and Acoustics, 2006, 128(4):555–567.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai, 200072, P. R. China

    Li Xiao-jun  (李晓军) & Chen Li-qun  (陈立群)

  2. Department of Mechanics, Shanghai University, Shanghai, 200444, P. R. China

    Chen Li-qun  (陈立群)

Authors
  1. Li Xiao-jun  (李晓军)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen Li-qun  (陈立群)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chen Li-qun  (陈立群).

Additional information

Contributed by CHEN Li-qun

Project supported by the National Natural Science Foundation of China (Nos. 10672092 and 10725209), the Scientific Research Project of Shanghai Municipal Education Commission (No. 07ZZ07), and Shanghai Leading Academic Discipline Project (No. Y0103)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, Xj., Chen, Lq. Modal analysis of coupled vibration of belt drive systems. Appl. Math. Mech.-Engl. Ed. 29, 9–13 (2008). https://doi.org/10.1007/s10483-008-0102-x

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-008-0102-x

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation