Skip to main content
SpringerLink
Log in

Delamination growth for composite laminated cylindrical shells under external pressure

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

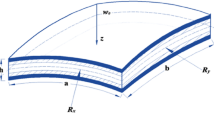
The delamination growth may occur in delaminated cylindrical shells under external pressure. This will lead to failure of structure. By using the variational principle of moving boundary and considering the contact effect between delamination regions, in this work, the delamination growth was investigated for cylindrical shells under the action of external pressure. At the same time, according to the Griffith criterion, the formulas of energy release rate along the delamination front were obtained. In the numerical calculation, the delamination growth of axisymmetrical laminated cylindrical shells was analyzed, and the effects of delamination sizes and depths, the geometrical parameters, the material properties, and the laminate stacking sequences on delamination growth were discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Chai H, Babcock C D, Knauss W. One dimensional modeling of failure in laminated plates by delamination buckling[J]. Journal of Solids and Structure, 1981, 17:1069–1083.

    Article  MATH  Google Scholar 

  2. Sallam S, Simitses G J. Delamination buckling and growth of flat, cross-ply laminates[J]. Composite Structure, 1985, 4:361–381.

    Article  Google Scholar 

  3. Yin W L. Axisymmetric buckling and growth of a circular delamination in a compressived laminate[J]. Int J Solids Structures, 1985, 21(5):503–514.

    Article  MATH  Google Scholar 

  4. Witcomb J D. Finite element analysis of instability related delamination growth[J]. J Composite Materials, 1981, 15:403–426.

    Article  Google Scholar 

  5. Zafer Kutlu, Fu-Kuo Chang. Modeling compression failure of laminated composites containing multiple through-the-width delaminations[J]. Journal of Composite Materials, 1992, 26(3):350–387.

    Article  Google Scholar 

  6. Chai H. Two-demensional modeling of compressive failure in delaminated laminates[J]. Journal of Composite Materials, 1985, 19(1):67–98.

    Article  Google Scholar 

  7. Whitcomb J D, Shivakumar K N. Strain-energy release rate analysis of plates with postbuckled delaminations[J]. Composite Structure, 1989, 23(7):714–734.

    Google Scholar 

  8. Whitcomb J D. Three-dimensional analysis of a postbuckled embedded delamination[J]. Composite Structure, 1989, 23(9):862–889.

    Google Scholar 

  9. Sheinman I, Kardomateas G K. Energy release rate and stress intensity factors for delaminated composite laminates[J]. Int J Solids Structures, 1997, 34:451–459.

    Article  MATH  Google Scholar 

  10. Davidson B D, Gharibian S J, Yu L J. Evaluation of energy release rate-based approaches for predicting delamination growth in laminated composites[J]. Int J Fracture, 2000, 105(4):343–365.

    Article  Google Scholar 

  11. Nillsson K F, Asp L E, Alpman J E, Nystdt L. Delamination buckling and growth for delaminations at different depths in a slender composite panel[J]. Int J Solids Structures, 2001, 38:3039–3071.

    Article  Google Scholar 

  12. Park O, Sanker B V. Crack-tip force method for computing energy release rate in delaminated plates[J]. Composite Structure, 2002, 55:429–434.

    Article  Google Scholar 

  13. Wang J L, Qiao P Z. On the energy release rate and mode mix of delaminated shear deformable composite plates[J]. Int J Solids Structures, 2004, 41:2757–2779.

    Article  MATH  Google Scholar 

  14. Zhang Xiangyang, Yu Shouwen. The analysis of axisymmetric buckling and growth of circular-shaped delamination[J]. Acta Mechanica Solida Sinica, 1996, 17(4):331–334 (in Chinese).

    Google Scholar 

  15. Jane K C, Liao H W, Wien Hong. Validation of the Rayleigh-Ritz method for the postbuckling analysis of rectangular plates with application to delamination growth[J]. Mechanics Research Communications, 2003, 30:531–538.

    Article  MATH  Google Scholar 

  16. Qian Weichang. Variational calculus and finite element[M]. Beijing: Science Press, 1980 (in Chinese).

    Google Scholar 

  17. Guo Ming. Axisymmetrical large deformation analysis of orthotropic laminated composite cylindrical shells[J]. Journal of Solid Rocket Technology, 1997, 20(2):61–67 (in Chinese).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mechanics and Aerospace, Hunan University, Changsha, 410082, P. R. China

    Fu Yi-ming  (傅衣铭) & Yang Jin-hua  (杨金花)

  2. College of Bridge and Structure Engineering, Changsha University of Science and Technology, Changsha, 410076, P. R. China

    Yang Jin-hua  (杨金花)

Authors
  1. Fu Yi-ming  (傅衣铭)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yang Jin-hua  (杨金花)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fu Yi-ming  (傅衣铭).

Additional information

Contributed by FU Yi-ming

Project supported by the National Natural Science Foundation of China (No. 10572049)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fu, Ym., Yang, Jh. Delamination growth for composite laminated cylindrical shells under external pressure. Appl Math Mech 28, 1131–1144 (2007). https://doi.org/10.1007/s10483-007-0901-1

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-007-0901-1

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation