Abstract
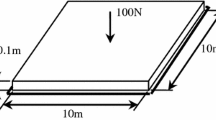
The finite strip controlling equation of pinned curve box was deduced on basis of Novozhilov theory and with flexibility method, and the problem of continuous curve box was resolved. Dynamic Bayesian error function of displacement parameters of continuous curve box was found. The corresponding formulas of dynamic Bayesian expectation and variance were derived. After the method of solving the automatic search of step length was put forward, the optimization estimation computing formulas were also obtained by adapting conjugate gradient method. Then the steps of dynamic Bayesian estimation were given in detail. Through analysis of a classic example, the criterion of judging the precision of the known information is gained as well as some other important conclusions about dynamic Bayesian stochastic estimation of displacement parameters of continuous curve box.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Xiang Haifan. Advanced theory of bridge structure[M]. Beijing: The Peoples’ Communications Press, 2001 (in Chinese).
Xiao Rucheng. Analysis of bridge structure and program system[M]. Beijing: The Peoples’ Communications Press, 2002 (in Chinese).
Ghani R A, Hangang U. Thin-walled multicell box-girder finite element[J]. Structure Engineering, ASCE, 1991, 117(10):2953–2971.
Martti J M, Jahn P. Finite element analysis of box girders[J]. Structure Division, ASCE, 1980, (10):1343–1357.
Zhao Zhenming, Chen Baochun. Analysis of pole system and box girder bridge and program designing[M]. Guangzhou: Huanan University of Science and Engineering Press, 1997 (in Chinese).
Zhang Youqi. Finite strip analysis of box girder bridge[M]. Beijing: The Peoples’ Communications Press, 1978 (in Chinese).
Gioda. Back analysis procedure for the interpretation of field measurements in geomechanics[J]. Numerical and Analytic Method in Geomechanics, 1987, (11):555–583.
Ohkami T, Ichikawa Y. A boundary element method for identifying orthotropic material parameters[J]. Numerical and Analytic Method in Geomechanics, 1991, (15):609–625.
Shu Shanhang. Parameter stochastic back analysis method and object oriented programming design[D]. M Sc Dissertation. Nanjing: Hohai University, 2000 (in Chinese).
Fan Mingyu, Zhang Yin. Basis of optimization technology[M]. Beijing: Tsinghua University Press, 1982 (in Chinese).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by FU Yi-ming
Rights and permissions
About this article
Cite this article
Zhang, J., Ye, Js. & Zhao, Xm. Dynamic Bayesian estimation of displacement parameters of continuous curve box based on Novozhilov theory. Appl Math Mech 28, 87–95 (2007). https://doi.org/10.1007/s10483-007-0110-z
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s10483-007-0110-z