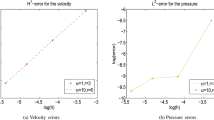
Abstract
Local and parallel finite element algorithms based on two-grid discretization for Navier-Stokes equations in two dimension are presented. Its basis is a coarse finite element space on the global domain and a fine finite element space on the subdomain. The local algorithm consists of finding a solution for a given nonlinear problem in the coarse finite element space and a solution for a linear problem in the fine finite element space, then droping the coarse solution of the region near the boundary. By overlapping domain decomposition, the parallel algorithms are obtained. This paper analyzes the error of these algorithms and gets some error estimates which are better than those of the standard finite element method. The numerical experiments are given too. By analyzing and comparing these results, it is shown that these algorithms are correct and high efficient.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Xu Jinchao. A novel two-grid method for semilinear equations[J]. SIAM J Sci Comput, 1994, 15(1):231–237.
Xu Jinchao. Two-grid discretization techniques for linear and nonlinear PDEs[J]. SIAM J Numer Anal, 1996, 33(5):1759–1777.
Xu Jinchao, Zhou Aihui. Local and parallel finite element algorithms based on two-grid discretizations[J]. Math Comp, 2000, 69(231):881–909.
Xu Jinchao, Zhou Aihui. Local and parallel finite elment algorithms based on two-grid discretizations for nonlinear problems[J]. Adv Comp Math, 2001, 14(4):293–327.
He Yinnian, Xu Jinchao, Zhou Aihui. Local and parallel finite element algorithms for the Stokes problem[J]. Numerische Mathematik, 2007, to be published.
Adams R. Sobolev space[M]. New York: Academic Press Inc, 1975.
Girault V, Raviart P A. Finite element methods for the Navier-Stokes equations: theory and algorithms[M]. Berlin: Springer-Verlag, 1986.
Ren Chunfeng, Ma Yichen. Two-grid error estimates for the stream function form of Navier-Stokes equations[J]. Applied Mathematics and Mechanics (English Edition), 2002, 23(7):773–782.
Ren Chunfeng, Ma Yichen, Ying Genjun. A two-grid method with backtracking technique for the Navier-Stokes equations[J]. Num Math J Chinese Uni, 2003, 25(3):193–204.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by ZHOU Zhe-wei
Project supported by the National Natural Science Foundation of China (No.10371096)
Rights and permissions
About this article
Cite this article
Ma, Fy., Ma, Yc. & Wo, Wf. Local and parallel finite element algorithms based on two-grid discretization for steady Navier-Stokes equations. Appl Math Mech 28, 27–35 (2007). https://doi.org/10.1007/s10483-007-0104-x
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s10483-007-0104-x