On a queueing inventory problem with necessary and optional inventories

Abstract

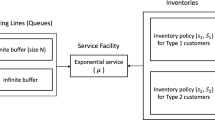
Queueing inventory models are extensively analysed since 1992. Very few among these discuss multi-commodity system. In this paper, we present a multi-commodity queueing inventory problem involving one essential and a set of m optional item(s). Immediately after the service of an essential item, the customer either leaves the system with probability p or with probability 1-p he goes for optional item(s). However, in the absence of an essential item, service will not be provided. More than one optional item can be demanded by the customer. The i th optional item or i th and j th optional items or i th, j th and k th and so on or all the optional items together, could be demanded by a customer, with probabilities $p_{i}$, $p_{ij}$, $p_{ijk}$ $\ldots$ $p_{12\ldots m}$ respectively. If the demanded optional item(s) is(are) not available, the customer leaves the system after purchasing the essential item. With the arrival of customers forming Markovian Arrival Process (MAP), service time of essential item Phase type distributed and that for optional items exponentially distributed( depending on the type(s) of item(s)), all given by the same (single) server, we analyse the system. Then we obtain the system state probability distribution. In-order to get a picture of how the system performs, we derive several characteristics of the system. With control policies for essential and optional items determined respectively, by (s, S) and ($s_{i}$,$S_{i}$),$i=1,2,3,$..., m, we investigate the optimal values of $s,S,s_{i}$ and $S_{i}$s’. To this end, we set up a cost function, involving these control variables.