Abstract
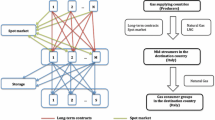
In Europe gas is sold according to two main methods: long-term contract (LTCs) and hub pricing. Europe is moving towards a mix of long term and spot markets, but the eventual outcome is still unknown. The fall of the European gas demand combined with the increase of the US shale gas exports and the rise of Liquefied Natural Gas availability on international markets have led to a reduction of the European gas hub prices. On the other side, oil-indexed LTCs failed to promptly adjust their positions, implying significant losses for European gas mid-streamers that asked for a re-negotiation of their existing contracts and obtained new contracts linked also to hub spot prices. The debate over the necessity of the oil-indexed pricing is still on-going. The supporters of the gas-indexation state that nowadays the European gas industry is mature enough to adopt hub-based pricing system. With the aim of analyzing this situation and determining whether oil-indexation can still be convenient for the European gas market, we consider both spot gas prices traded at the hub and oil-based commodities as possible underlyings of the LTCs. We investigates the dependence risk and the optimal resource allocation of the underlying assets of a gas LTC through pair-vine copulas and portfolio optimization methods with respect to five risk measures. Our results show that European LTCs will most likely remain indexed to oil-based commodities, even though a partial dependence on spot hub prices is conceded.




Similar content being viewed by others
Notes
The liquidity of a gas hub can be defined as the ratio between the total volume of trade on the hub and the volume of gas consumed in the area served by the hub.
Copula family type: 0 = Independence copula; 1 = Gaussian copula; 2 = Student-t copula (t-copula); 3 = Clayton copula; 5 = Frank copula; 13 = Rotated Clayton copula (180 degrees); 14 = Rotated Gumbel copula (180 degrees); 16= Rotated Joe copula (180 degrees).
References
Aas, K., Czado, C., Frigessi, A., & Bakken, H. (2009). Pair-copula constructions of multiple dependence. Insurance: Mathematics and Economics, 44, 182–198.
Abada, I., Ehrenmann, A., & Smeers, Y. (2017). Modeling gas markets with endogenous long-term contracts. Operations Research, 65(4), 856–877.
Accioly, R. M. S., & Aiube, F. A. L. (2008). Analysis of crude oil and gasoline prices through copulas. Cadernos do IME- Série Estatìstica, 24, 5–28.
Aloui, R., Ben Aïssa, M. S., & Nguyen, D. K. (2013). Conditional dependence structure between oil prices and exchange rates: A copula-garch approach. Journal of International Money and Finance, 32, 719–738.
Arreola Hernandez, J. (2014). Are oil and gas stocks from the Australian market riskier than coal and uranium stocks? Dependence risk analysis and portfolio optimization. Energy Economics, 45, 528–536.
Bassetti, F., De Giuli, M. E., Nicolino, E., & Tarantola, C. (2018). Multivariate dependence analysis via tree copula models: An application to one-year forward energy contracts. European Journal of Operational Research, 269, 1107–1121.
Bedford, T., & Cooke, R. M. (2001). Probability density decomposition for conditionally dependent random variables modeled by vines. Annals of Mathematics and Artificial Intelligence, 32, 245–268.
Bedford, T., & Cooke, R. M. (2002). vines- a new graphical model for dependent random variables. Annals of Statistics, 30, 1031–1068.
Bekiros, S., Hernandez, J. A., Hammoudeh, S., & Nguyen, D. K. (2015). Multivariate dependence risk and portfolio optimization: An application to mining stock portfolios. Resources Policy, 46, 1–11.
Brechmann, E. C., & Czado, C. (2013). Risk management with high-dimensional vine copulas: An analysis of the Euro Stoxx 50. Statistics & Risk Modeling, 30, 307–342.
Chekhlov, A., Uryasev, S., & Zabarankin, M. (2005). Drawdown measure in portfolio optimization. International Journal of Theoretical and Applied Finance, 8, 13–58.
Chyong, C.-K. (2015). Markets and long-term contracts: The case of Russian gas supplies to Europe. EPRG working paper (p. 1524).
Clarke, K. A. (2007). A simple distribution-free test for nonnested model selection. Political Analysis, 15, 347–363.
Czado, C., Min, A., Baumann, T., & Dakovic, R. (2009). Pair-copula constructions for modeling exchange rate dependence. Preprint available at https://mediatum.ub.tum.de/1079184. Accessed Nov 2016.
Czado, C., Schepsmeier, U., & Min, A. (2012). Maximum likelihood estimation of mixed C-vines with application to exchange rates. Statistical Modelling, 12(3), 229–255.
Dalla, Valle L., De Giuli, M. E., Tarantola, C., & Manelli, C. (2016). Default probability estimation via pair-copula constructions. European Journal of Operational Research, 249, 298–311.
Dickey, D., & Fuller, W. (1981). Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica, 49, 1057–1072.
Dißmann, J., Brechmann, E., Czado, C., & Kurowicka, D. (2013). Selecting and estimating regular vine copulae and application to financial returns. Computational Statistics & Data Analysis, 59, 52–69.
Durante, F., & Sempi, C. (2015). Principles of copula theory. London: Chapman and Hall/CRC.
Fisher, T. J., & Gallagher, C. M. (2012). New weighted portmanteau statistics for time series goodness of fit testing. Journal of the American Statistical Association, 107(498), 777–787.
Franza, L. (2014). Long-term gas import contracts in Europe. In CIEP paper (Vol. 8). Available at http://www.clingendaelenergy.com/inc/upload/files/Ciep_paper_2014-08_web_1.pdf. Accessed Nov 2016.
Frisch, M. (2010). Current European gas pricing problems: Solutions based on price review and price reopener provisions. In International energy law and policy research paper series, no. 3.
Gaupp, F., Pflug, G., Hochrainer-Stigler, S., Hall, J., & Dadson, S. (2017). Dependency of crop production between global breadbaskets: A copula approach for the assessment of global and regional risk pools. Risk Analysis, 37(11), 2212–2228.
Genest, C., & Favre, A. C. (2007). Everything you always wanted to know about copula modeling but were afraid to ask. Journal of Hydrologic Engineering, 12, 347–368.
Genest, C. M., Gendron, M., & Bourdeau-Brien, M. (2009). The advent of copulas in finance. The European Journal of Finance, 15, 609–618.
GIIGNL. (2018). The LNG industry. Available at https://giignl.org/publications#webform-client-form-1161. Accessed April 2018.
Grégoire, V., Genest, C., & Gendron, M. (2008). Using copulas to model price dependencies in energy markets. Energy Risk, 5, 58–64.
Heather, P. (2012). Continental European gas hubs: Are they fit for purpose? (p. 63). Oxford: Oxford Institute for Energy Studies.
Heather, P., & Petrovich, B. (2017). European traded gas hubs: An updated analysis on liquidity, maturity and barriers to market integration. In The Oxford Institute for energy studies paper-energy insight (Vol. 13).
Hofert, M., Kojadinovic, I., Maechler, M., & Yan, J. (2017). Package copula. Available http://copula.r-forge.r-project.org/. Accessed April 2018.
IEA (International Energy Agency). (2013). Developing a natural gas trading hub in Asia-obstacles and opportunities. Available https://www.iea.org/publications/freepublications/publication/AsianGasHub_FINAL_WEB.pdf. Accessed Nov 2016.
Jäschke, S. (2014). Estimation of risk measures in energy portfolios using modern copula techniques. Computational Statistics and Data Analysis, 76, 359–376.
Joe, H. (1996). Families of m-variate distributions with given margins and m(m-1)/2 bivariate dependence parameters. In IMS lecture notes (Vol. 76, pp. 359–376).
Joe, H. (1997). Multivariate model and dependence concepts. Monographs on statistics an applied probability (Vol. 73). London: Chapman, Hall.
Konno, H., Shirakawa, H., & Yamazaki, H. (1993). A mean-absolute deviation-skewness portfolio optimization models. Annals of Operations Research, 45(1), 205–220.
Krzemienowski, A., & Szymczyk, S. (2016). Portfolio optimization with a copula-based extension of conditional value-at-risk. Annals of Operations Research, 237(1–2), 219–236.
Kwiatkowski, D., Phillips, P. C. B., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54, 159–178.
Kurowicka, D., & Cooke, R. (2006). Uncertainty analysis with high dimensional dependence modelling. Chichester: Wiley.
Li, X., & You, Y. (2014). A note on allocation of portfolio shares of random assets with Archimedean copula. Annals of Operations Research, 212(1), 155–167.
Lu, X. F., Lai, K. K., & Liang, L. (2014). Portfolio value-at-risk estimation in energy futures markets with time-varying copula-GARCH model. Annals of Operations Research, 219, 333–357.
Mandelbrot, B. B. (1963). The variation of certain speculative prices. The Journal of Business, 36, 394–419.
Markowitz, H. (1952). Portfolio selection. The Journal of Finance, 7(1), 77–91.
Melling, A. J. (2010). Natural gas pricing and its future-Europe ad the battleground. Carnegie Endowment for international peace. Available at http://carnegieendowment.org/files/gas_pricing_europe.pdf. Accessed Nov 2016.
Morales-Nápoles, O. (2010). Counting vines. In D. Kurowicka & H. Joe (Eds.), Dependence modeling: Vine copula handbook (pp. 189–218). World Scientific.
Nelsen, R. B. (1999). An introduction to copulas. In Lecture notes in statistics (Vol. 139). New York: Springer.
Phillips, P. C. B., & Perron, P. (1988). Testing for unit roots in time series regression. Biometrika, 75, 335–346.
Reboredo, J. C. (2011). How do crude oil prices co-move? A copula approach. Energy Economics, 33, 95–113.
Rockafellar, R. T., & Uryasev, S. (2000). Optimization of conditional value-at-risk. Journal of Risk, 2, 21–42.
Saida, A. B., & Prigent, J. (2018). On the robustness of portfolio allocation under copula misspecification. Annals of Operations Research, 262(2), 631–652.
Schepsmeier, U. (2016). A goodness-of-fit test for regular vine copula models. Econometric Reviews. https://doi.org/10.1080/07474938.2016.1222231.
Schepsmeier, U., & Czado, C. (2016). Dependence modelling with regular vine copula models: A case-study for car crash simulation data. Journal of the Royal Statistical Society: Series C (Applied Statistics), 65(3), 415–429.
Schepsmeier, U., Stoeber, J., Brechmann, E. C., Graeler, B., Nagler, T., & Erhardt, T. (2018). vineCopula: Statistical inference of vine copulas. Available at http://CRAN.R-project.org/package=vineCopula. Accessed April 2018.
Sklar, M. (1959). Fonctions de répartition á ndimensions et leurs marges. Publications de l’Institut de Statistique de l’Université de Paris, 8, 229–231.
Stern, J., & Rogers, H. V. (2014). The dynamics of a liberalised European gas market: Key determinants of hub prices, and roles and risks of major players. In The Oxford Institute for energy studies (Vol. 94). Available at http://www.oxfordenergy.org/wpcms/wp-content/uploads/2014/12/NG-94.pdf. Accessed Nov 2016.
Tran, H. D., Pham, U. H., Ly, S., & Vo-Duy, T. (2017). Extraction dependence structure of distorted copulas via a measure of dependence. Annals of Operations Research, 256(2), 221–236.
Theisen, N. (2014). Natural gas pricing in the EU: From oil-indexation to a hybrid pricing system. Regional Centre for energy policy research. Available at http://rekk.hu/downloads/projects/2014_rekk_natural%20gas%20pricing.pdf. Accessed Nov 2017.
Vuong, Q. H. (1989). Ratio tests for model selection and non-nested hypotheses. Econometrica, 57, 307–333.
Wen, X., Wei, Y., & Huang, D. (2012). Measuring contagion between energy market and stock market during financial crisis: A copula approach. Energy Economics, 34, 1435–1446.
Xunpeng, S. (2016). Gas and LNG pricing and trading hub in East Asia: An introduction. Natural Gas Industry B, 3, 352–356.
Yafimava, K. (2014). Outlook for the long term contracts in a globalizing market (focus on Europe). Presentation available at http://www.unece.org/fileadmin/DAM/energy/se/pp/geg/gif5_19Jan2015/s1_1_Yafimava.pdf. Accessed Nov 2016.
Young, M. R. (1998). A minimax portfolio selection rule with linear programming solution. Management Science, 44, 673–683.
Acknowledgements
We are grateful to the Editor and the anonymous referees for valuable comments. The work of the author M.E. De Giuli has been partially supported by MIUR, Italy, PRIN MISURA 2010RHAHPL. E. Allevi and G. Oggioni are grateful to the UniBS H&W Project “Brescia 20-20-20” for the financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Allevi, E., Boffino, L., De Giuli, M.E. et al. Analysis of long-term natural gas contracts with vine copulas in optimization portfolio problems. Ann Oper Res 274, 1–37 (2019). https://doi.org/10.1007/s10479-018-2932-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-2932-x