Skip to main content
SpringerLink
Log in

Analysis of multistage amplifiers with hybrid cascode feedforward compensation using a modified model for load impedance

  • Published:
Analog Integrated Circuits and Signal Processing Aims and scope Submit manuscript

Abstract

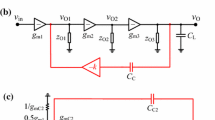
Hybrid cascode feedforward compensation (HCFC) is an effective technique to stabilize nano-scale three-stage amplifiers driving ultra-large load capacitors. It divides the compensation capacitance and shares it between two high-speed local feedback loops embedded within the amplifier core. In this article, a systematic approach to analyze the transfer function and to evaluate the pole expressions of nano-scale HCFC amplifiers is presented. For the first time, the equivalent output impedance is successfully modeled to approximate the complicated transfer function of the HCFC amplifier without the need for lengthy pencil-and-paper calculations. An HCFC amplifier is designed and simulated in 90-nm CMOS technology, to verify the effectiveness of the new analytic approach. The simulated transfer function of the amplifier is almost identical to a calculated transfer function derived based on the new model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Carusone, T. C., Johns, D. A., & Martin, K. W. (2011). Analog integrated circuit design. Hoboken: Wiley.

    Google Scholar 

  2. Leung, K. N., & Mok, P. K. T. (2001). Analysis of multistage amplifier-frequency compensation. IEEE Transactions on Circuits and Systems I, 48(8), 1041–1056.

    Article  Google Scholar 

  3. Mesri, A., Javidan, J., & Pirbazari, M. M. (2015). High gain two-stage amplifier with positive capacitive feedback compensation. IET Circuits, Devices and Systems, 9(3), 181–190.

    Article  Google Scholar 

  4. Bult, K., & Geelen, G. J. G. M. (1990). A fast-settling CMOS opamp for SC circuits with 90 dB DC gain. IEEE Journal of Solid-Slate Circuits, 25(6), 1379–1384.

    Article  Google Scholar 

  5. Aminzadeh, H. (2017). Evaluation of the pole expressions of nano-scale multistage amplifiers based on equivalent output impedance. International Journal of Electronics and Communications, 72, 243–251.

    Article  Google Scholar 

  6. Razavi, B. (2001). Design of analog CMOS integrated circuits. New York: McGraw-Hill.

    Google Scholar 

  7. Eschauzier, R. G. H., & Huijsing, J. H. (1995). Frequency compensation techniques for low-power operational amplifiers. Boston, MA: Kluwer.

    Book  Google Scholar 

  8. Ahuja, B. K. (1983). An improved frequency compensation technique for CMOS operational amplifiers. IEEE Journal of Solid-State Circuits, 18(6), 629–633.

    Article  Google Scholar 

  9. Leung, K. N., Mok, P. K. T., Ki, W. H., & Sin, J. K. O. (2000). Three-stage large capacitive load amplifier with damping-factor-control frequency compensation. IEEE Journal of Solid-State Circuits, 35(2), 221–230.

    Article  Google Scholar 

  10. Lee, H., & Mok, P. K. T. (2003). Active-feedback frequency compensation technique for low power multistage amplifiers. IEEE Journal of Solid-State Circuits, 38(3), 511–520.

    Article  Google Scholar 

  11. Fan, X., Mishra, C., & Sinencio, E. S. (2005). Single Miller capacitor frequency compensation technique for low-power multistage amplifiers. IEEE Journal of Solid-State Circuits, 40(3), 584–592.

    Article  Google Scholar 

  12. Peng, X., & Sansen, W. (2005). Transconductance with capacitances feedback compensation for multistage amplifiers. IEEE Journal of Solid-State Circuits, 40, 1514–1520.

    Article  Google Scholar 

  13. Aminzadeh, H., Danaie, M., & Lotfi, R. (2008). Design of high-speed two-stage cascode compensated operational amplifiers based on settling time and open-loop parameters. Integration, the VLSI, 41(2), 183–192.

    Article  Google Scholar 

  14. Aminzadeh, H. (2011). Three-stage nested-Miller-compensated operational amplifiers: Analysis, design, and optimization based on settling time. International Journal of Circuit Theory and Applications, 39(6), 573–587.

    Article  Google Scholar 

  15. Chong, S. S., & Chan, P. K. (2012). Cross feedforward cascode compensation for low-power three-stage amplifier with large capacitive load. IEEE Journal of Solid-State Circuits, 47(9), 2227–2234.

    Article  Google Scholar 

  16. Aminzadeh, H., Rakhshanizadeh, E., & Emamjomeh, H. (2014). Hybrid cascode compensation with feedforward stage for high-speed area-efficient three-stage CMOS amplifiers. Analog Integrated Circuits and Signal Processing, 78(1), 253–256.

    Article  Google Scholar 

  17. Aminzadeh, H., & Banihashemi, M. (2014). Miller compensation: optimal design for operational amplifiers with a required settling time. Circuits, Systems and Signal Processing, 33(9), 2675–2694.

    Article  Google Scholar 

  18. Yan, Z., Mak, P. I., & Martins, R. P. (2011). Two-stage operational amplifiers: Power-and-area-efficient frequency compensation for driving a wide range of capacitive load. IEEE Circuits and Systems Magazine, 11(1), 26–42.

    Article  Google Scholar 

  19. Yan, Z., Mak, P. I., Law, M. K., & Martins, R. P. (2012). Ultra-area-efficient three-stage amplifier using current buffer Miller compensation and parallel compensation. IET Electronics Letters, 48, 624–626.

    Article  Google Scholar 

  20. Yan, Z., Mak, P. I., Law, M. K., & Martins, R. P. (2013). A 0.016-mm2 144-µW three-stage amplifier capable of driving 1-to-15 nF capacitive load with > 0.95-MHz GBW. IEEE Journal of Solid-State Circuits, 48, 527–540.

    Article  Google Scholar 

  21. Tan, M., & Ki, W. H. (2015). A cascode Miller-compensated three-stage amplifier with local impedance attenuation for optimized complex-pole control. IEEE Journal of Solid-State Circuits, 50(2), 440–449.

    Article  Google Scholar 

  22. Aminzadeh, H., & Dashti, A. (2015). Hybrid cascode compensation with current amplifiers for nano-scale three-stage amplifiers driving heavy capacitive loads. Analog Integrated Circuits and Signal Processing, 83, 331–341.

    Article  Google Scholar 

  23. Qin, C., Zhang, L., Zhou, C., Zhang, L., Wang, Y., & Yu, Z. (2017). Dual AC boosting compensation scheme for multistage amplifiers. IEEE Transactions on Circuits and Systems I: Express Briefs, 64(8), 882–886.

    Google Scholar 

  24. Luchetta, A., Manetti, S., & Reatti, A. (2001). SAPWIN-a symbolic simulator as a support in electrical engineering education. IEEE Transaction on Education, 44(2), 213.

    Article  Google Scholar 

  25. Rutenbar, R., Gielen, G., & Antao, B. (2009). ISAAC: A symbolic simulator for analog integrated circuits. Computer-Aided Design of Analog Integrated Circuits and Systems, 24(6), 276–286.

    Google Scholar 

  26. Shokouhifar, M., & Jalali, A. (2017). Simplified symbolic transfer function factorization using combined artificial bee colony and simulated annealing. Applied Soft Computing, 55, 436–451.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Payame Noor University, Tehran, 19395-3697, Iran

    Hamed Aminzadeh

Authors
  1. Hamed Aminzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamed Aminzadeh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aminzadeh, H. Analysis of multistage amplifiers with hybrid cascode feedforward compensation using a modified model for load impedance. Analog Integr Circ Sig Process 95, 271–282 (2018). https://doi.org/10.1007/s10470-018-1179-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10470-018-1179-4

Keywords

Search

Navigation