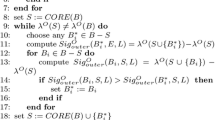Abstract
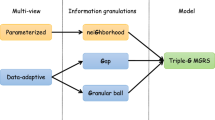
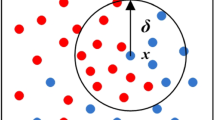
In recent years, more and more methods and theories of multi-granulation information systems have been explored. However, there is very limited investigation on the attribute reducts of multi-granulation rough sets. Therefore, the main objective of this paper is to draw attention to the attribute reducts of multi-granulation information system. For any subset of information system, we usually characterize it by its upper and lower approximations. In order to calculate the upper and lower approximations faster, we must reduce the redundant information of the information system. According to the preceding analysis, we first introduce three types of attribute reduct, which are called arbitrary union reduct, neighborhood union reduct and neighborhood intersection reduct, respectively. Then many basic and important results of these reducts are deeply explored. In order to apply the theories of attribute reducts to deal with practical issues, we develop three algorithms so as to compute multi-granulation upper and lower approximations. Next, we further study the interrelationships among these attribute reducts. Finally, we present a multi-granulation information system with respect to thirty students’ exam scores and calculate the corresponding attribute reducts by using the algorithms listed in the paper.
Similar content being viewed by others
References
Abualigah L, Khader A, Hanandeh E (2018) Hybrid clustering analysis using improved krill herd algorithm. Appl Intell 48(11):4047–4071
Abualigah L, Khader A, Hanandeh E (2018) A combination of objective functions and hybrid krill herd algorithm for text document clustering analysis. Eng Appl Artif Intell 73:111–125
Abualigah L, Khader A, Hanandeh E (2018) A novel weighting scheme applied to improve the text document clustering techniques. Innovative computing, optimization and its applications. Springer, Cham, pp 305–320
Abualigah L, Khader A, Hanandeh E (2018) A hybrid strategy for krill herd algorithm with harmony search algorithm to improve the data clustering. intelligent decision technologies, preprint
Abualigah L, Khader A, Hanandeh E (2017) A new feature selection method to improve the document clustering using particle swarm optimization algorithm. J Comput Sci 25:456–466
Abualigah L, Khader A, Hanandeh E, Gandomi A (2017) A novel hybridization strategy for krill herd algorithm applied to clustering techniques. Appl Soft Comput 60:423–435
Abualigah L, Khader A, Al-Betar M, Hanandeh E (2017) A new hybridization strategy for krill herd algorithm and harmony search algorithm applied to improve the data clustering. Management 9:11
Abualigah L, Khader A (2017) Unsupervised text feature selection technique based on hybrid particle swarm optimization algorithm with genetic operators for the text clustering. J Supercomput 73(11):4773–4795
Abualigah L, Khader A, Al-Betar M, Alomari O (2017) Text feature selection with a robust weight scheme and dynamic dimension reduction to text document clustering. Expert Syst Appl 84:24–36
Abualigah L, Hanandeh E (2015) Applying genetic algorithms to information retrieval using vector space model. Int J Comput Sci Eng Appl 5(1):19
Al-Betar M, Abualigah L (2017) Big data and E-government: a review. In: The 8th IEEE international conference on information technology (ICIT). Amman, Jordan
Bonikowski Z, Bryniarski E, Wybraniec U (1998) Extensions and intentions in the rough set theory. Inf Sci 107:149–167
Baszczyński J, Slowiński R, Szelag M (2011) Sequential covering rule induction algorithm for variable consistency rough set approaches. Inf Sci 181(5):987–1002
Cattaneo G (1998) Abstract approximate spaces for rough theories. In: Polkowski Skowron (ed) Rough sets in knowledge discovery 1: methodology and applications. Physicaverlag, Heidelberg, pp 59–98
Chen D, hang W, Yeung D, Tsang E (2006) Rough approximation on a complete completely distributive lattice with applications to generalized rough sets. Inf Sci 176:1829–1848
Chen D, Wang C, Hu Q (2007) A new approach to attribute reduction of consistent and inconsistent covering decision systems with covering rough sets. Inf Sci 177(17):3500–3518
Chen D, Hu Q, Yang Y (2011) Parameterized attribute reduction with Gaussian kernel based fuzzy rough sets. Inf Sci 181(23):5169–5179
Chen J, Li J, Lin Y, Lin G, Ma Z (2015) Relations of reduction between covering generalized rough sets and concept lattices. Inf Sci 304:16–27
Diker M, Ugur A (2012) Textures and covering based rough sets. Inf Sci 184(1):44–63
Ge X, Li Z (2011) Definable subsets in covering approximation spaces. Int J Comput Math Sci 5(1):31–34
Kong Q, Xu W (2018) The comparative study of covering rough sets and multi-granulation rough sets. Soft Comput. https://doi.org/10.1007/s00500-018-3205-y
Kong Q, Xu W (2018) Operation properties and algebraic application of covering rough sets. Fundam Inf 160:385–408
Kong Q, Zhang X, Xu W (2018) Operation properties and algebraic properties of multi-covering rough sets. Granul Comput. https://doi.org/10.1007/s41066-018-0137-y
Kong Q, Wei Z (2017) Further study of multi-granulation fuzzy rough sets. J Intell Fuzzy Syst 32:2413–2424
Kong Q, Wei Z (2015) Covering-based fuzzy rough sets. J Intell Fuzzy Syst 29:2405–2411
Li J, Ren Y, Mei C, Qian Y, Yang X (2016) A comparative study of multi-granulation rough sets and concept lattices via rule acquisition. Knowl Based Syst 91:152–164
Li J, Huang C, Qi J, Qian Y, Liu W (2017) Three-way cognitive concept learning via multi-granularity. Inf Sci 378:244–263
Lin G, Liang J, Qian Y (2013) Multigranulation rough sers: from partition to covering. Inf Sci 241:101–118
Liu C, Wang M (2011) Covering fuzzy rough set based on multi-granulation. In: International conference on uncertainty reasoning and knowledge engineering. pp 146–149
Liu C, Miao D, Qian J (2014) On multi-granulation covering rough sets. Int J Approx Reason 55:1404–1418
Liu G, Zhu W (2008) The algebraic structures of generalized rough set theory. Inf Sci 178:4105–4113
Liu G, Sai Y (2009) A comparison of two types of rough sets induced by coverings. Int J Approx Reason 50:521–528
Pawlak Z (1982) Rough sets. Int J Comput Inf Sci 11(5):341–356
Qian Y, Liang J, Yao Y, Dang C (2010) MGRS: a multi-granulation rough set. Inf Sci 180:949–970
Qian Y, Liang J (2006) Rough set method based on multi-granulations, In: The 5th IEEE international conference on congnitive informatics. Beijing, China
She Y, he X (2003) On the structure of the multigranulation rough set model. Knowl Based Syst 151:81–92
Shi Z, Gong Z (2010) The futher investigation of covering-based rough sets: uncertainty characterization, similarity measure and generalized models. Inf Sci 180(19):3745–3763
Skowron A, Stepaniuk J (1996) Tolerance approximation spaces. Fundam Inf 27:245–253
Slowinski R, Vanderpooten D (2000) A generalized definition of rough approximations based on similarity. IEEE Trans Knowl Data Eng 12:331–336
Tan A, Li J, Lin Y (2015) Matrix-based set approximations and reductions in covering decision systems. Int J Approx Reason 59:68–80
Tsang E, Chen D, Yeung D (2008) Approximations and reducts with covering generalized rough sets. Comput Math Appl 56:279–289
Wang C, He Q, Chen D, Hu Q (2014) A novel method for attribute reduction of covering decision systems. Inf Sci 254:181–196
Wang C, Shao M, Sun B (2015) An improved attribute reduction scheme with covering based rough sets. Appl Soft Comput 26:235–243
Wang C, Shao M, He Q, Qian Y, Qi Y (2016) Feature subset selection based on fuzzy neighborhood rough sets. Knowl Based Syst 111(1):173–179
Wang C, Hu Q, Wang X, Chen D, Qian Y (2017) Feature selection based on neighborhood discrimination index. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2710422
Wang C, He Q, Shao M, Xua Y, Hu Q (2017) A unified information measure for general binary relations. Knowl Based Syst 135(1):18–28
Xu W, Li Y, Liao X (2012) Approaches to attribute reductions based on rough set and matrix computation in inconsistent ordered information systems. Knowl Based Syst 41(5):78–91
Xu W, Wang Q, Zhang X (2011) Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space. Int J Fuzzy Syst 13:246–259
Xu W, Wang Q, Zhang X (2013) Multi-granulation rough sets based on tolerance relations. Soft Comput 17(7):1241–1252
Xu W, Wang Q, Luo S (2014) Multi-granulation fuzzy rough sets. J Intell Fuzzy Syst 26:1323–1340
Xu W, Li W, Zhang X (2017) Generalized multigranulation rough sets and optimal granularity selection. Granul Comput. https://doi.org/10.1007/s41066-017-0042-9
Yang X, Song X, Dou H, Yang J (2011) Multigranulation rough set: from crisp to fuzzy case. Ann Fuzzy Math Inf 1:55–70
Yao Y (2011) Information granulation and rough set approximation. Int J Intell Syst 16(1):87–104
Yao Y (1998) Constructive and algebraic methods of the theory of rough sets. Inf Sci 109:21–47
Zakowski W (1983) Approximations in the space (\(u,\pi \)). Demonstr Math 16:761–769
Zhang X, Kong Q (2016) On four types of multi-covering rough sets. Fundam Inf 147:457–476
Zhu W, Wang F (2003) Reduction and axiomization of covering generalized rough sets. Inf Sci 152:217–230
Acknowledgements
The authors are very grateful to the reviewers and editors for their valuable suggestions. This work is partially supported by National Natural Science Foundation of China (Nos.61472463, 61772002, 61402064), Fundamental Research Funds for the Central Universities (XDJK2019B029), Natural Science Foundation of Fujian Province (Nos. 2017J01763, 2017J01468, 2016J01310, 2016J01735, 2018J01538) and Research Startup Foundation of Jimei University (NO. ZQ2017004), Foundation of Education Department of Fujian Province, China (No. JAT160369).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kong, Q., Zhang, X., Xu, W. et al. Attribute reducts of multi-granulation information system. Artif Intell Rev 53, 1353–1371 (2020). https://doi.org/10.1007/s10462-019-09699-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-019-09699-3