Skip to main content
SpringerLink
Log in

Stability in barter exchange markets

  • Published:
Autonomous Agents and Multi-Agent Systems Aims and scope Submit manuscript

Abstract

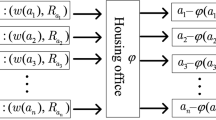
The notion of stability is the foundation of several classic problems in economics and computer science that arise in a wide-variety of real-world situations, including Stable Marriage, Stable Roommate, Hospital Resident and Group Activity Selection. We study this notion in the context of barter exchange markets. The input of our problem of interest consists of a set of people offering goods/services, with each person subjectively assigning values to a subset of goods/services offered by other people. The goal is to find a stable transaction, a set of cycles that is stable in the following sense: there does not exist a cycle such that every person participating in that cycle prefers to his current “status”. For example, consider a market where families are seeking vacation rentals and offering their own homes for the same. Each family wishes to acquire a vacation home in exchange of its own home without any monetary exchange. We study such a market by analyzing a stable transaction of houses involving cycles of fixed length. The underlying rationale is that an entire trade/exchange fails if any of the participating agents cancels the agreement; as a result, shorter (trading) cycles are desirable. We show that given a transaction, it can be verified whether or not it is stable in polynomial time, and that the problem of finding a stable transaction is NP-hard even if each person desires only a small number of other goods/services. Having established these results, we study the problem of finding a stable transaction in the framework of parameterized algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. Note that for a fixed exchange X, there is exactly one outgoing arc and exactly one incoming arc incident on every vertex in X.

  2. Note that u’s evaluation of v’s property is scalable based on u’s evaluation of the various attributes of v’s property.

References

  1. Abraham, D. J., Blum, A., & Sandholm, T. (2007). Clearing algorithms for barter exchange markets: Enabling nationwide kidney exchanges. In Proceedings of the 8th ACM conference on electronic commerce (EC) (pp. 295–304).

  2. Anderson, R., Ashlagi, I., Gamarnik, D., & Roth, A. E. (2015). Finding long chains in kidney exchange using the traveling salesman problem. In Proceedings of the National Academy of Sciences (Vol. 112, pp. 663–668).

  3. Biró, P. (2007). Stable exchange of indivisible goods with restrictions. In Proceedings of the 5th Japanese-Hungarian Symposium (pp. 97–105). Citeseer.

  4. Brandt, F., Conitzer, V., Endrisss, U., Lang, J., & Procaccia, A. D. (Eds.). (2016). Handbook of computational social choice. Cambridge: Cambridge University Press.

    MATH  Google Scholar 

  5. Brandt, F., & Geist, C. (2016). Finding strategyproof social choice functions via SAT solving. Journal of Artificial Intelligence Research (JAIR), 55, 565–602.

    Article  MathSciNet  MATH  Google Scholar 

  6. Cygan, M., Fomin, F. V., Kowalik, L., Lokshtanov, D., Marx, D., Pilipczuk, M., et al. (2015). Parameterized algorithms. Berlin: Springer.

    Book  MATH  Google Scholar 

  7. Dickerson, J., Manlove, D., Plaut, B., Sandholm, T., & Trimble, J. (2016). Position-indexed formulations for kidney exchange. In Proceedings of EC.

  8. Diestel, R. (2012). Graph theory (4th ed., Vol. 173)., Graduate texts in mathematics Berlin: Springer.

    MATH  Google Scholar 

  9. Downey, R. G., & Fellows, M. R. (1995). Fixed-parameter tractability and completeness II: On completeness for W[1]. Theoretical Computer Science, 141(1&2), 109–131.

    Article  MathSciNet  MATH  Google Scholar 

  10. Drummond, J., Perrault, A., & Bacchus, F. (2015). Sat is an effective and complete method for solving stable matching problems with couples. In Proceedings of IJCAI.

  11. Fomin, F. V., Lokshtanov, D., Panolan, F., & Saurabh, S. (2016). Efficient computation of representative families with applications in parameterized and exact algorithms. Journal of the ACM, 63(4), 29:1–29:60.

    Article  MathSciNet  MATH  Google Scholar 

  12. Gale, D., & Shapley, L. S. (1962). College admissions and the stability of marriage. The American Mathematical Monthly, 69(1), 9–15.

    Article  MathSciNet  MATH  Google Scholar 

  13. Garey, M. R., & Johnson, D. S. (1979). Computers and intractability: A guide to the theory of NP-completeness. New York: W.H. Freeman.

    MATH  Google Scholar 

  14. Gusfield, D., & Irving, R. W. (1989). The stable marriage problem: Structure and algorithms., Foundations of computing series Cambridge: MIT Press.

    MATH  Google Scholar 

  15. Igarashi, A., Bredereck, R., & Elkind, E. (2017). On parameterized complexity of group activity selection problems on social networks. In Proceedings of AAMAS’17.

  16. Igarashi, A., & Elkind, E. (2016). Hedonic games with graph-restricted communication. In Proceedings of AAMAS’16 (pp. 242–250).

  17. Igarashi, A., Elkind, E., & Peters, D. (2017). Group activity selection on social network. In Proceedings of AAAI’17.

  18. Intervac: www.intervac-homeexchange.com.

  19. Irving, R. W. (2007). The cycle roommates problem: A hard case of kidney exchange. Information Processing Letters, 103(1), 1–4.

    Article  MathSciNet  MATH  Google Scholar 

  20. Irving, R. W. (1994). Stable marriage and indifference. Discrete Applied Mathematics, 48(3), 261–272.

    Article  MathSciNet  MATH  Google Scholar 

  21. Irving, R., Iwama, K., Manlove, D. F., Miyazaki, S., & Morita, Y. (2002). Hard variants of stable marriage. Theoretical Computer Science, 276(1–2), 261–279.

    MathSciNet  MATH  Google Scholar 

  22. Knuth, D. E. (1997). Stable marriage and its relation to other combinatorial problems : An introduction to the mathematical analysis of algorithms. In CRM proceedings & lecture notes. Providence, RI: American Mathematical Society.

  23. Manlove, D. F. (2013). Algorithmics of matching under preferences (Vol. 2)., Series on theoretical computer science Singapore: World Scientific.

    Book  MATH  Google Scholar 

  24. McBride, I. (2015). Complexity results and integer programming models for hospitals/residents problem variants. Ph.D. thesis, University of Glasgow.

  25. NationalOddShoeExchange: http://www.oddshoe.org/.

  26. ReadItSwapIt: http://www.readitswapit.co.uk/thelibrary.aspx.

  27. Sonmez, T. (1999). Strategy-proofness and essentially single-valued cores. Econometrica, 67(3), 677–689.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank anonymous reviewers for their valuable comments and suggestions which helped to improve the paper.

Author information

Authors and Affiliations

  1. National Institute for Science Education and Research, HBNI, Jatni, India

    Sushmita Gupta

  2. Department of Informatics, University of Bergen, Bergen, Norway

    Fahad Panolan

  3. The Institute of Mathematical Sciences, HBNI, Chennai, India

    Saket Saurabh

  4. Ben-Gurion University of the Negev, Beersheba, Israel

    Meirav Zehavi

Authors
  1. Sushmita Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fahad Panolan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Saket Saurabh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Meirav Zehavi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sushmita Gupta.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

F. Panolan: This work is supported by the European Research Council (ERC) via Grant LOPPRE, Reference 819416 and Norwegian Research Council via Project MULTIVAL.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, S., Panolan, F., Saurabh, S. et al. Stability in barter exchange markets. Auton Agent Multi-Agent Syst 33, 518–539 (2019). https://doi.org/10.1007/s10458-019-09414-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10458-019-09414-0

Keywords

Search

Navigation