Abstract
The optimal coalition structure determination problem is in general computationally hard. In this article, we identify some problem instances for which the space of possible coalition structures has a certain form and constructively prove that the problem is polynomial time solvable. Specifically, we consider games with an ordering over the players and introduce a distance metric for measuring the distance between any two structures. In terms of this metric, we define the property of monotonicity, meaning that coalition structures closer to the optimal, as measured by the metric, have higher value than those further away. Similarly, quasi-monotonicity means that part of the space of coalition structures is monotonic, while part of it is non-monotonic. (Quasi)-monotonicity is a property that can be satisfied by coalition games in characteristic function form and also those in partition function form. For a setting with a monotonic value function and a known player ordering, we prove that the optimal coalition structure determination problem is polynomial time solvable and devise such an algorithm using a greedy approach. We extend this algorithm to quasi-monotonic value functions and demonstrate how its time complexity improves from exponential to polynomial as the degree of monotonicity of the value function increases. We go further and consider a setting in which the value function is monotonic and an ordering over the players is known to exist but ordering itself is unknown. For this setting too, we prove that the coalition structure determination problem is polynomial time solvable and devise such an algorithm.
Similar content being viewed by others
1 Introduction
One of the fundamental problems in multiagent systems and in game theory is that of determining an optimal coalition structure, i.e., a partition of a set of n agents into disjoint coalitions so as to optimize the value of the partition. The value of a partition is specified in terms of the values of its constituent coalitions. The value of a coalition, in turn, may be defined in several ways [30]. One possibility is to define the value of a coalition solely in terms of its members. In cooperative game theory, such scenarios are called characteristic function games (CFGs) [7]. In the computer science literature, the corresponding optimal coalition structure determination problem is referred to as the complete set partitioning problem [22]. Alternatively, the value of a coalition can be defined in terms of the entire partition in which the coalition is embedded. In cooperative game theory, such scenarios are referred to as partition function games (PFGs) [40].
The general problem of optimal coalition structure determination involves combinatorial search over a space whose size is exponential in the number of agents, which renders brute force search approach computationally infeasible. In practice though, the search space is not always unstructured—often there is some form of inherent regularity in at least a part of, if not the whole space. For example, consider the airline crew scheduling problem, which requires organising staff into coalitions based on individual characteristics, and optimally scheduling the coalitions. The players, i.e., the crew, are ordered in that any non-optimal placement of an individual in the early part of a schedule can propagate down the chain and reduce the value of the entire partition. It is entirely possible that the earlier in the schedule a non-optimality is introduced, the greater the reduction in the value of the partition as a whole, relative to the optimum (see Sect. 8 for details). In other words, the search space is structured in that there is a relation between the degree of closeness between a partition and the optimum, and the value of that partition. The greater the closeness, the higher the value. The aim of our research is to find an effective way of expressing such regularities, in order to facilitate the development of computationally feasible methods for computing an optimal coalition structure.
To this end, we consider games with a player ordering and introduce a distance metric for measuring how close any two partitions are. In terms of this metric, we define a property of value functions that we refer to as monotonicity. Intuitively, monotonicity means that coalition structures that are closer to the optimum (when measured using the distance metric) have higher value than those further away. We also consider quasi-monotonicity. A function v is quasi-monotonic if it is monotonic for a part of the space but non-monotonic for the remaining space. This latter property can be satisfied by any kind of value function (i.e., non-separable,Footnote 1 CFGs, and PFGs). The degree of monotonicity, (equivalently non-monotonicity), of a value function is measured in terms of the diameter of the set of all optimal partitions. The diameter ranges between 0 and 1; at one extreme the diameter is 0 when the value function is monotonic over the entire search space. As the diameter increases, that part of the search space for which the value function is monotonic successively decreases in size while the remaining part for which the value function is non-monotonic increases, reaching the other extreme at diameter equal to 1, when the value function is non-monotonic over the entire search space.
Against this background, the main contributions of this paper are as follows:
-
1.
Introducing a metric to measure the distance between any two partitions and defining the property of monotonicity.
-
2.
For monotonic value functions and a known player ordering, proving that the optimal coalition structure determination problem is polynomial time solvable and devising such an algorithm using a greedy approach.
-
3.
Extending the above mentioned greedy algorithm to allow quasi-monotonic functions and demonstrating how its time complexity improves from exponential to polynomial as the degree of monotonicity of the value function increases.
-
4.
For monotonic value functions and an unknown player ordering, proving that the optimal coalition structure determination problem is polynomial time solvable and devising such an algorithm.
Placing our contribution in the context of existing literature, we note that a great deal of research has been devoted to the coalition structure generation problem, but most of it has focused on the complete set partitioning problem, with even the best solutions having exponential time complexity. As for PFGs, the search space is considerably larger relative to CFGs. Some recent literature has dealt with restricted cases of PFGs: in [28] either positive only or negative only externalities are allowed but not both, while in [3] mixed externalities are considered but only for one specific value function. In other research [37], the computational complexity is overcome by imposing restrictions on the size of coalitions that can form. Section 9 provides a detailed account of related literature. Our research advances the state of art in that we introduce a distance metric and the property of monotonicity which can be satisfied by three different types of search spaces: CFGs, PFGs (with positive only, negative only, and mixed externalities), and non-separable value functions. CFGs and PFGs provide a general prototype for modelling a number of combinatorial optimization problems [9]. The proposed framework preserves this generality; both the distance metric and the property of monotonicity are abstract notions which can be used to capture application specific features.
In particular, the key distinctive features of the proposed methods are:
-
1.
Unlike existing methods, they are suitable for any kind of value function (i.e., non-separable, CFGs, and PFGs with positive only, negative only, and mixed externalities) that satisfies monotonicity.
-
2.
Unlike existing methods, they require only an ordering on the values of partitions to be known but not their actual values. The methods in literature require the actual value of each coalition to be known, and assume that the value function is separable in that the value of each partition is simply the sum of the values of the coalitions in it. The proposed methods are therefore practically more relevant because it is easier to know an ordering over the values of partitions but much harder to know their exact values, especially for large games.
The remainder of the article is organised as follows. We start in Sect. 2 by presenting notation and defining notions related to coalition structures. Section 3 introduces the distance metric. We then present algorithms for computing optimal coalition structures for three different settings:
-
Section 4 considers a setting with a monotonic value function, a known player ordering, and a unique optimum.
-
Section 5 considers a setting with a monotonic value function, a known player ordering, and multiple optima.
-
Section 6 considers a setting with quasi-monotonic values and multiple optima.
-
Section 7 considers a setting with a monotonic value function, an unknown player ordering, and a unique optimum.
Section 8 is a discussion of some applications of the proposed methods. Section 9 places this research in the context of related literature and Sect. 10 is the concluding section. Table 1 is summary of notation.
2 The model
We assume a finite, non-empty set of players\(N = \{1, \ldots , n\}\). A coalition, C, is simply a subset of N, i.e., \(C\subseteq N\). We will denote the set \(\{1, \ldots , i\}\) by [i].
A central concept in our work is the notion of a coalition structure. Intuitively, a coalition structure captures the idea of the players N dividing into separate coalitions, and conventionally, a coalition structure is therefore simply defined as a partition of N [7]. Without any loss of generality, assume that the coalitions in a structure \(\pi \) are ordered by the following principle:
coalition \(C_i\) will precede a coalition \(C_j\) in \(\pi \) if the smallestFootnote 2 element of \(C_i\) is less than the smallest element of \(C_j\).
Note that since coalitions in a coalition structure are assumed to be mutually disjoint, then this ordering is guaranteed to be strict.
Example 1
Suppose  . Then the following are examples of possible coalition structures over N:
. Then the following are examples of possible coalition structures over N:
However, the following are not legal coalition structures over N, according to our definition:
-
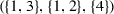 —because player 1 is a member of more than one coalition;
—because player 1 is a member of more than one coalition; -
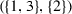 —because player 4 does not appear in any coalition;
—because player 4 does not appear in any coalition; -
 —because
—because 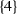 appears before
appears before 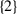 ;
; -
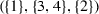 —because
—because 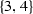 appears before
appears before 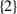 .
.
\(\square \)
Formally, we have:
Definition 1
A coalition structure \(\pi = (C_1, C_2, \ldots , C_M)\) over N is a sequence of coalitions \(C_i \subseteq N\) such that:
-
1.
\(\bigcup _{1 \le i \le M} C_i = N\),
-
2.
\(C_i \cap C_j = \emptyset \text {for} 1 \le i \le M , 1 \le j \le M \text { s.t.} i \ne j\), and
-
3.
for \(1 \le i \le M\) and \(1 \le j \le M\), if \(i < j\) then \(\min C_i < \min C_j\).
with the convention \(\min \emptyset = \infty \).
Let \(\varPi _N\) denote the set of all coalition structures over N. We will use the terms coalition structure, sequence, and partition synonymously.
Observe that, defined in this way, coalition structures have the following property. In any coalition structure, player 1 must belong to the first coalition, player 2 must belong to one of the first two coalitions, and so on. In general, if the players \(1, \ldots , i\)\((1 \le i < n)\) belong to the first \(1 \le m \le i\) non-empty coalitions of any sequence, then player \(i+1\) must belong to one of the first \(m+1\) coalitions in it.
We find it useful to work with a functional representation of coalition structures, which we call the sequence form. A sequence form representation is simply a function that maps a given player i to the index of the coalition of which i is a member.
Example 2
Let  and let \({\textsc {SF}} : N \rightarrow N\) be a function such that \({\textsc {SF}}(1) = 1\), \({\textsc {SF}}(2) = 2\), \({\textsc {SF}}(3) = 3\), and \({\textsc {SF}}(4) = 2\). Then this sequence form function defines the coalition structure
and let \({\textsc {SF}} : N \rightarrow N\) be a function such that \({\textsc {SF}}(1) = 1\), \({\textsc {SF}}(2) = 2\), \({\textsc {SF}}(3) = 3\), and \({\textsc {SF}}(4) = 2\). Then this sequence form function defines the coalition structure  . \(\square \)
. \(\square \)
More generally, it is useful to work with sequence form functions that only define coalition membership for some subset of the overall set of agents:
Definition 2
For \(1 \le k \le n\), a sequence form\({\textsc {SF}}_{k}: [k] \rightarrow N\) maps each player \(i \in [k]\) to the index of a coalition in a sequence. An instance of\({\textsc {SF}}_{k}\) is any coalition structure \(\pi \) of N that satisfies the condition
In general, there may be multiple instances of a sequence form function \({\textsc {SF}}_k\) and we will write
to denote the fact that \(\pi \) is an instance of \({\textsc {SF}}_k\). For ease of representation, we will sometimes write a sequence form as an n-element vector where the ith element gives the index of the coalition to which player i belongs, or is written as − if the position of player i is not given. For example, for \(n=4\), \(SF_2 = (1, 1, -, -)\) indicates that players 1 and 2 belong to the first coalition but the positions of players 3 and 4 are not given.
Example 3
For \(N=\{1, 2, 3, 4\}\), the sequence function \(SF_2\) with \(SF_2(1)=1\) and \(SF_2(2)=1\) specifies the coalitions to which players 1 and 2 belong. Possible instances of this form are:
For the sequence form \(SF_3 = (1, 2, 1, -)\), \(max(SF_3) = 2\). \(\square \)
Each coalition structure has a value given by a function v:
A pair (N, v) constitutes a coalition game. Given a coalition game, the problem is to find an optimal sequence\(\pi ^{\textsc {opt}}\) such that:
This problem is, in general, computationally hard because of the huge search space. For a game of n players, the number of all possible coalition structures is given by Bell(n) [4, 31]:
with \(Bell(0)=Bell(1)=1\). Since \(Bell(n) \sim \varTheta (n^n)\) [10], it is, in general, infeasible to compute an optimal coalition structure by exhaustive search over the space of all coalition structures. Against this background, the aim of our research is to identify specific classes of value functions that are practically relevant and for which the coalition structure generation problem can be solved in polynomial time.
In general, there are two specific classes of value functions:
-
1.
A partition value function v is separable [13] if it is the sum of the values of its constituent coalitions. If \(v_C\) denotes the value of coalition C, then the overall value of a coalition structure \(\pi \) is defined as:
$$\begin{aligned} v(\pi )= & {} \underset{C \in \pi }{\sum } \quad v_C \end{aligned}$$(1)where \(v_C\) denotes the value of \(C \subseteq N\). This is the most commonly used function in the literature. Separable functions may, in turn, be further classified into two types:
-
(a)
The first possibility is that the value of each coalition depends only on the makeup of that coalition. In this case, and with a slight abuse of notation, we assume that a value function for coalitions simply takes the form
$$\begin{aligned} v_C : \quad 2^N\rightarrow & {} \mathbb {R}. \end{aligned}$$This definition of value function corresponds to coalition games in characteristic function form [7], for which the optimal sequence problem is nothing but the well-known complete set partitioning problem [20].
-
(b)
A second possibility is that the value of a coalition depends not just on the makeup of that coalition, but also on the other coalitions present in the partition [30]. Here, with another abuse of notation, we can think of the value function for coalitions as taking the following form.
$$\begin{aligned} v_C: \quad 2^N \times \varPi _N\rightarrow & {} \mathbb {R}\end{aligned}$$(2)The value of a coalition now depends not just on the make up of the coalition in question, but also on how the external players (i.e., those outside the coalition) are organized. For example, for \(N=\{1, 2, 3, 4\}\), the value of the coalition \(\{1, 2\}\) will depend on how players 3 and 4 are organized. Thus, the value \(v(\{1, 2\}, (\{1, 2\}, \{3, 4\}))\) may not be equal to \(v(\{1, 2\}, (\{1, 2\}, \{3\}, \{4\}))\). This definition of value function corresponds to coalition games in partition function form.
-
(a)
-
2.
A partition value function v is non-separable if it is not separable.
In what follows, we will consider both separable and non-separable functions that are quasi-monotonic. Quasi-monotonicity will be defined in terms of a distance metric on the space \(\varPi _N\) of possible coalition structures.
3 A distance metric
The metric we consider is defined in terms of the notion of restriction of a partition to a coalition.
Definition 3
The restriction\(\pi _{|[i]}\) of a coalition structure \(\pi = (C_1, C_2, \ldots )\) to coalition [i] is defined as
For readability, any empty sets will not be shown in \(\pi _{|[i]} \).
Example 4
Suppose \(N = \{1,2,3,4\}\) and \(\pi = (\{1,2,3\}, \{4\})\). The restriction of \(\pi \) to [2] is
We will eliminate the empty set and write this simply as \(\pi _{|[2]} = (\{1,2\})\). \(\square \)
For any two coalition structures over N, we have the following readily established property.
Lemma 1
Let \(\pi ^1 \in \varPi _N\) and \(\pi ^2\in \varPi _N\) be any two coalition structures over  . Then \(\exists u \in \mathbb {N}\) such that \(\pi ^1_{|[u]} = \pi ^2_{|[u]}\).
. Then \(\exists u \in \mathbb {N}\) such that \(\pi ^1_{|[u]} = \pi ^2_{|[u]}\).
Lemma 1 can be proved easily by letting \(u=1\). Intuitively, the larger the value of u, then the “closer” \(\pi ^1\) and \(\pi ^2\) are together. This motivates the introduction of the following distance metricd, which gives a measure of the distance between any two elements in \(\varPi _N\):
where
Example 5
For \(N=\{1, 2, 3, 4\}\), Table 2 lists some pairs of coalition structures and the distances between them. \(\square \)
Then the diameter of a set \(\varPi \subseteq \varPi _N\) is defined as follows.
Definition 4
The diameter\({\mathcal {D}}\) of a set \(\varPi \subseteq \varPi _N\) is the maximum distance between any pair of points in \(\varPi \):
We will now prove that a pair \((\varPi _N, d)\) defines a metric space, which is bounded and such that \({\mathcal {D}}(\varPi _N) = 1\).
Theorem 1
For two arbitrary sequences \(\pi ^1 \in \varPi _N\) and \(\pi ^2 \in \varPi _N\) we have the following assertions:
-
1.
If \(\pi ^1 = \pi ^2\) then \(\varDelta (\pi ^1,\pi ^1) = \infty \) and so \(d(\pi ^1,\pi ^1) = 0\).
-
2.
If \(\pi ^1 \ne \pi ^2\) then \(\varDelta (\pi ^1,\pi ^2) \in \{1, \ldots , n-1\}\) and \(d(\pi ^1,\pi ^2) \in \{\frac{1}{n-1}, \frac{1}{n-2}, \ldots , 1\}\).
Proof
Consider the first case, i.e., \(\pi ^1 = \pi ^2\). Let \(\pi ^1=(C^1_1, C^1_2, \ldots )\) and \(\pi ^2=(C^2_1, C^2_2, \ldots )\). If \(\pi ^1=\pi ^2\) then \(\pi ^1_{|[i]} = \pi ^2_{|[i]}\) for all \(i \ge 1\), so \(\varDelta (\pi ^1,\pi ^2) = \infty \) and \(d(\pi ^1,\pi ^2) = 0\).
Consider the second case, i.e., \(\pi ^1 \ne \pi ^2\). Let z be such that \(C^1_i = C^2_i\) for \(1 \le i \le z-1\) and \(C^1_z \ne C^2_z\). Then, as per the principle (given in Sect. 2) used to order coalitions in a partition, the least element in \(C^1_z\) will be identical to the least element in \(C^2_z\). Let s be this least element where \(1 \le s \le n\) and \(s=1\) iff \(z=1\). Observe that \(s=n\) implies that \(C^1_z = \{n\}\), and since \(C^1_i = C^2_i\) for \(1 \le i \le z-1\), the coalition \(C^2_z\) must be identical to the coalition \(C^1_z\), i.e., \(\pi ^1=\pi ^2\). Thus we need only consider the cases \(1 \le s \le n-1\). Let \(1 \le k \le n-s\) be such that either of the following two conditions is true:
-
1.
\(\{s, \ldots , s+k\} \subseteq C^1_z\), and \(\{s, \ldots , s+k-1\} \subseteq C^2_z\) and \(s+k \notin C^2_z\).
-
2.
\(\{s, \ldots , s+k\} \subseteq C^2_z\), and \(\{s, \ldots , s+k-1\} \subseteq C^1_z\) and \(s+k \notin C^1_z\).
Without any loss of generality, assume that the former is true. Then we get
Substitute \(s=1\) in (5), to get \(\varDelta (\pi ^1,\pi ^2) = k\). Since \(1 \le k \le n-s\), we get \(\varDelta (\pi ^1,\pi ^2) \in \{1, \ldots , n-1\}\) and \(d(\pi ^1,\pi ^2) \in \{\frac{1}{n-1}, \ldots , 1\}\). Substitute \(s=2\) in (5), to \(\varDelta (\pi ^1,\pi ^2) = k+1\). Since \(1 \le k \le n-s\), we get \(\varDelta (\pi ^1,\pi ^2) \in \{2, \ldots , n-1\}\) and \(d(\pi ^1,\pi ^2) \in \{\frac{1}{n-1} , \ldots , \frac{1}{2}\}\). In general, for any s, we get \(\varDelta (\pi ^1,\pi ^2) \in \{s, \ldots , n-1\}\) and \(d(\pi ^1,\pi ^2) \in \{\frac{1}{n-1}, \ldots , \frac{1}{s}\}\). \(\square \)
We have referred to the function d as a distance metric. We now show that this terminology is justified, in the sense that d satisfies all metric axioms, viz., non-negativity, symmetry, and the triangle inequality [39]:
-
Non-negativity:
This axiom requires that, for two arbitrary points x and y in the set \(\varPi _N\), \(d(x,y) \ge 0\) and \(d(x,y)=0 \Leftrightarrow x=y\).
-
Symmetry:
For two arbitrary points x and y in \(\varPi _N\), \(d(x,y) = d(y,x)\).
-
Triangle inequality:
For three arbitrary points x, y, and z in \(\varPi _N\), \(d(x,z) \le d(x,y) + d(y,z)\).
Theorem 2 proves that the distance function satisfies the above axioms.
Theorem 2
The distance function defined in (3) satisfies all metric axioms.
Proof
Non-negativity follows from Theorem 1: \(d(\pi ^1,\pi ^2) \in \{\frac{1}{n-1}, \frac{1}{n-2}, \ldots , 1\} \cup \{0\}\). Further, for any two structures, \(\pi ^1\) and \(\pi ^2\), \(d(\pi ^1, \pi ^2) = 0\) implies that \(\pi ^1=\pi ^2\) and \(\pi ^1=\pi ^2\) implies \(d(\pi ^1, \pi ^2) = 0\). As per (3), the distance function is symmetric because \(\varDelta \) [see (4)] is symmetric.
To prove the triangle inequality axiom, consider three distinct arbitrary sequences \(\pi ^1=(C^1_1, C^1_2, \ldots )\), \(\pi ^2=(C^2_1, C^2_2, \ldots )\), and \(\pi ^3=(C^3_1, C^3_2, \ldots )\) with distances as shown in Fig. 1. The triangle inequality axiom requires that \(d_1 \le d_2 + d_3\), i.e.,
For any \(\varDelta (\pi ^1,\pi ^2)\) and any \(\varDelta (\pi ^2,\pi ^3)\), \(\varDelta (\pi ^1,\pi ^3)\) must be the minimum of \(\varDelta (\pi ^1,\pi ^2)\) and \(\varDelta (\pi ^2,\pi ^3)\), i.e., the following equality must be true:
It now follows that (6) must be true both if \(min(\varDelta (\pi ^1,\pi ^2), \varDelta (\pi ^2,\pi ^3)) =\varDelta (\pi ^1,\pi ^2)\) and also if \(min(\varDelta (\pi ^1,\pi ^2), \varDelta (\pi ^2,\pi ^3)) = \varDelta (\pi ^2,\pi ^3)\). \(\square \)
Theorem 3 establishes that no sequence is equidistant from any two points that are distance one apart. This result will be used later in the construction of the search method.
Theorem 3
Consider two points \(\pi ^1\) and \(\pi ^2\) such that \(d(\pi ^1, \pi ^2)=1\). Then, \(\lnot \exists \pi ^3\) such that \(d(\pi ^1, \pi ^3)=d(\pi ^2, \pi ^3)\).
Proof
Given that \(d(\pi ^1, \pi ^2)=1\), \(\pi ^1=(C^1_1, C^1_2, \ldots )\) and \(\pi ^2=(C^2_1, C^2_2, \ldots )\) must be in one of the following two forms [see (4)]:
-
1.
Players 1 and 2 both belong to the same coalition in \(\pi ^1\) (i.e., \(\{1, 2\} \subseteq C^1_1\)) and to different coalitions in \(\pi ^2\) (i.e., \(1 \in C^2_1\) and \(2 \in C^2_2\)).
-
2.
Players 1 and 2 both belong to the same coalition in \(\pi ^2\) (i.e., \(\{1, 2\} \subseteq C^2_1\)) and to different coalitions in \(\pi ^1\) (i.e., \(1 \in C^1_1\) and \(2 \in C^1_2\)).
Without any loss of generality, we will assume that the first one is true. For the sequence \(\pi ^3=(C^3_1, C^3_2, \ldots )\), there are two possibilities with regard to players 1 and 2: either \(\{1,2\} \subseteq C^3_1\) or else \(1 \in C^3_1\) and \(2 \in C^3_2\). Consider the former case. As per (4), \(\varDelta (\pi ^1, \pi ^3) \ge 2\) and \(\varDelta (\pi ^2, \pi ^3) = 1\). Since \(\varDelta (\pi ^1, \pi ^3) \ne \varDelta (\pi ^2, \pi ^3)\), it is impossible for \(\pi ^3\) to be equidistant from \(\pi ^1\) and \(\pi ^2\).
Next, consider the case \(1 \in C^3_1\) and \(2 \in C^3_2\). As per (4), \(\varDelta (\pi ^2, \pi ^3) \ge 2\) and \(\varDelta (\pi ^1, \pi ^3) = 1\). Since \(\varDelta (\pi ^1, \pi ^3) \ne \varDelta (\pi ^2, \pi ^3)\), it is impossible for \(\pi ^3\) to be equidistant from \(\pi ^1\) and \(\pi ^2\).
\(\square \)
3.1 Uniqueness and monotonicity
In subsequent sections, we present algorithms for games that satisfy (or do not satisfy) the following two assumptions:
- \(A_1\) Uniqueness::
-
There is only one optimal sequence.
- \(A_2\) Monotonicity::
-
The function \(v: \varPi _N \rightarrow \mathbb {R}\) is monotonically decreasing in the distance of a sequence from the optimum \(\pi ^{\textsc {opt}}\), i.e., for two arbitrary sequences \(\pi ^1\) and \(\pi ^2 \ne \pi ^1\), we have the following implication:
$$\begin{aligned} d(\pi ^{\textsc {opt}}, \pi ^1) < d(\pi ^{\textsc {opt}}, \pi ^2)\Rightarrow & {} v(\pi ^1) > v(\pi ^2) \end{aligned}$$(7)
Lemma 2
For \(1 \le i < n\), any sequence in which the first mis-placed player is \(i+1\) (i.e., the players \(1, \ldots , i\) are correctly placed in their respective optimal coalitions but not player \(i+1\)) has a higher value than any sequence in which the first mis-placed player is i (i.e., the players \(1, \ldots , i-1\) are correctly placed in their respective optimal coalitions but not player i).
Proof
Let \(\pi ^1\) be a sequence in which the first mis-placed player is \(i+1\) and \(\pi ^2\) be a sequence in which the first mis-placed player is i. Since \(d(\pi ^{\textsc {opt}}, \pi ^1) < d(\pi ^{\textsc {opt}}, \pi ^2)\), \(v(\pi ^1) > v(\pi ^2)\). \(\square \)
Lemma 2 leads to the definition of player priority.
Definition 5
Each player has a priority: player 1 has the highest priority and the priority of any \(1 \le i <n\) is higher than that of player \(i+1\), i.e., \(1 \succ 2, \ldots , \succ n\).
Letting \(P_i\) (\(1 \le i \le n\)) denote priority i player, we have \(P_i = i\).
3.2 Externalities and distance
Let us consider the application of the distance metric to partition function games (PFGs). We consider three types of externalities in PFGs: positive only, negative only, and positive and negative externalities. Externalities are positive (negative) only if \(v(C, \pi ^1) \ge v(C, \pi ^2)\) for each embeddedFootnote 3 coalition \((C, \pi ^1)\) and \((C, \pi ^2)\) such that \(\pi ^1\) is coarserFootnote 4 (finer) than \(\pi ^2\) [11, 40].
Example 6
Table 3 is an illustration of the application of the distance metric to the three types of externalities. The value of a coalition is given by (2) and that of a partition by (1). Table 3(a) is for a PFG with positive only externalities. Consider the singleton coalition \(\{1\}\). There are two possible structures \(\{1\}\) could be embedded in: \((\{1\}, \{2\}, \{3\})\) and \((\{1\}, \{2, 3\})\). Since the latter is coarser than the former, \(v_C(\{1\}, (\{1\}, \{2, 3\})) > v_C(\{1\}, (\{1\}, \{2\}, \{3\}))\). In the same way, the condition for positive externalities is satisfied by other entries in the table.
Table 3(b) is for a PFG with negative only externalities. Table 3(c) is for a PFG with a combination of positive and negative externalities. Since \(v_C(\{1\}, (\{1\}, \{2, 3\})) < v_C(\{1\}, (\{1\}, \{2\}, \{3\}))\) in Table 3(c), the externality on \(\{1\}\) due to the merger of coalitions \(\{2\}\) and \(\{3\}\) is negative. At the same time, since \(v_C(\{2\}, (\{1, 3\}, \{2\})) > v_C(\{2\}, (\{1\}, \{2\}, \{3\}))\), the externality on \(\{2\}\) due to the merger of coalitions \(\{1\}\) and \(\{3\}\) is positive. \(\square \)
Lemma 3 proves the existence of value functions that satisfy both uniqueness and monotonicity properties.
Lemma 3
There exist separable and non-separable value functions that satisfy both monotonicty and uniqueness.
Proof
Consider first a separable value function of the form given in (1). For three player PFGs with positive only externalities, the value function in Table 3(a) satisfies both monotonicity and uniqueness. For negative only externalities, the value function in Table 3(b) satisfies both monotonicity and uniqueness. For mixed externalities, the value function in Table 3(c) satisfies both monotonicity and uniqueness.
Now, consider a non-separable value function of the following form:
For 3-player PFGs with positive only externalities, the value function in Table 4(a) satisfies both monotonicity and uniqueness. For negative only externalities, the value function in Table 4(b) satisfies both monotonicity and uniqueness. For mixed externalities, the value function in Table 4(c) satisfies both monotonicity and uniqueness. \(\square \)
4 Unique optimum, monotonic values, and a known player ordering
In this section, we consider the problem of computing an optimal coalition structure \(\pi ^{\textsc {opt}}= (C^\textsc {opt}_1, C^\textsc {opt}_2, \ldots )\) in games with a known player ordering and under the assumptions \(A_1\) (uniqueness) and \(A_2\) (monotononicity). In later sections, we will consider cases where these assumptions do not hold: the assumption \(A_1\) will be dropped in Sect. 5 to allow multiple optima, and \(A_2\) will be relaxed in Sect. 6. Then, in Sect. 7, we will consider a setting with unknown player ordering.
For a unique optimum, monotonic values, and a known player ordering, we will prove that the optimal coalition structure determination problem is polynomial time solvable and show how to compute the optimum in polynomial time. Theorem 4, built on Lemma 4, is the main result of this section.
The method for determining \(\pi ^{OPT}\) works as follows. Because of the coalition ordering principle given in Sect. 2, we know that player 1 must belong to \(C^{OPT}_1\). Knowing this, we find the coalition in \(\varPi ^{OPT}\) to which player 2 must belong. Then, on the basis of the coalitions to which players 1 and 2 belong, we find the coalition to which player 3 must belong. In general, we determine the coalition for any player \(1< i < n\) on the basis of the coalitions of the players 1 to \(i-1\). \(SF^{\textsc {OPT}}\) will denote a sequence form for \(\pi ^{OPT}\).
More precisely, suppose that we know the coalitions in \(\pi ^{\textsc {opt}}= (C^\textsc {opt}_1, C^\textsc {opt}_2, \ldots )\) to which each of the players \(1, \ldots , i-1\) (where \(i-1 < n\)) belongs but do not know the coalitions to which the players \(i, \ldots , n\) belong, i.e., we know the optimal sequence form \(SF^{\textsc {OPT}}_{i-1}\). Based on this knowledge, we can draw certain conclusions about the coalitions to which player i will possibly belong. These deductions are characterized in Lemma 4.
Lemma 4
For a unique optimum and monotonic value function, suppose the coalition in \(\pi ^{\textsc {opt}}=(C^{\textsc {opt}}_1, C^{\textsc {opt}}_2, \ldots )\) to which each of the the players in \(\{1, \ldots , i-1\}\), where \(i-1 \le n-1\), belongs is known. Let m be such that at least one of the first \(i-1\) players belongs to \(C^{\textsc {opt}}_m\) but none of them belong to any of the coalitions \(C^{\textsc {opt}}_{m+1}, C^{\textsc {opt}}_{m+2}, \ldots \). Then, player i must belong to a unique coalition \(C^{\textsc {opt}}_p\) where \(C^{\textsc {opt}}_p \in \{C^{\textsc {opt}}_1, \ldots , C^{\textsc {opt}}_{m+1}\}\). Further, for two arbitrary sequence forms \(SF^1_i(k)\) and \(SF^2_i(k)\) such that \(SF^1_i(k) = SF^{\textsc {OPT}}_i(k)\) for \(1 \le k \le i\) and \(SF^2_i(k) = SF^{\textsc {OPT}}_i(k)\) for \(1 \le k \le i-1\) and \(SF^2_i(i) \ne SF^{\textsc {OPT}}_i(i)\), and two arbitrary sequences \(\pi ^1 = (C^1_1, C^1_2, \ldots )\) and \(\pi ^2 = (C^2_1, C^2_2, \ldots )\) such that \(\pi ^1 \models SF^1_i\) and \(\pi ^2 \models SF^2_i\), the following implication must be true:
Proof
Because of the ordering on the coalitions in any sequence, player i must belong to a coalition in \(\{C^{\textsc {opt}}_1, \ldots , C^{\textsc {opt}}_{m+1}\}\). The fact that player i belongs to a unique coalition in \(\{C^{\textsc {opt}}_1, \ldots , C^{\textsc {opt}}_{m+1}\}\) is a consequence of the uniqueness assumption \(A_1\).
From the definition of \(\pi ^1\) and \(\pi ^2\) given in the statement of the lemma, player i is in the optimal position in \(\pi ^1\) but not in \(\pi ^2\) (i.e., if \(i \in C^{\textsc {opt}}_p\), then \(i \in C^1_p\) and \(i \notin C^2_p\)). We therefore get \(\varDelta (\pi ^{\textsc {opt}}, \pi ^1) \ge i\) and \(\varDelta (\pi ^{\textsc {opt}}, \pi ^2) = i-1\). That is, if \(i \in C^{\textsc {opt}}_p\), \(\pi ^1\) is closer to \(\pi ^{\textsc {opt}}\) than is \(\pi ^2\), so by monotonicity assumption, the value of \(\pi ^1\) must be greater than the value of \(\pi ^2\). \(\square \)
The intuitive meaning of Lemma 4 is that the value of any sequence in which the players \(1, \ldots , i\) belong to that coalition to which they belong in \(\pi ^{\textsc {OPT}}\) is greater than the value of any sequence in which only the players \(1, \ldots , i-1\) belong to the coalition to which they belong in \(\pi ^{\textsc {OPT}}\). Example 7 is an illustration of Lemma 4.
Example 7
Suppose the set of players is \(N=\{1, 2, 3, 4\}\). It is known that player 1 (2) belongs to the first (second) coalition in \(\pi ^{\textsc {opt}}\), i.e., \(\{1\} \subseteq C^{\textsc {opt}}_1\) and \(\{2\} \subseteq C^{\textsc {opt}}_2\). Given this, player 3 must belong to any one of the first three coalitions in \(\pi ^{\textsc {opt}}\), i.e., there are three possibilities for \(SF_3\): \((1, 2, 1, -)\), or \((1, 2, 2, -)\), or \((1, 2, 3, -)\). From these sequence forms, we get the instances \((1, 2, 1, -) \models \pi ^1\), \((1, 2, 2, -) \models \pi ^2\), and \((1, 2, 3, -) \models \pi ^3\) and the following implications:

\(\square \)
For the purpose of determining an optimal partition, it is not necessary to know the function v (i.e., the actual values of the partitions). It is enough to know if the value of a partition is higher/ lower than another partition. This will become evident in the proof of Theorem 4.
Theorem 4
If the optimum is unique and the value function monotonic, the optimal sequence \(\pi ^{\textsc {opt}}\) can be determined in \({\mathcal {O}}(n^3)\) time.
Proof
The position of player 1: Because of the coalition ordering principle for sequences, we know that player 1 must belong to the first coalition of any sequence, i.e., we have \(1 \in C^{\textsc {opt}}_1\). This takes \({\mathcal {O}}(1)\) time.
The position of player 2: Since \( 1 \in C^{\textsc {opt}}_1\), by Lemma 4, player 2 must belong either to \(C^{\textsc {opt}}_1\) or to \(C^{\textsc {opt}}_2\). Consider the sequence \(\pi ^1=(\{1, 2\ldots , n\})\) comprised of the single grand coalition and the sequence \(\pi ^2=(\{1\}, \{2\}, \ldots , \{n\})\) of n singletons. The values of \(\pi ^1\) and \(\pi ^2\) can be related in one of the following three ways:
-
1.
\(v(\pi ^1) = v(\pi ^2)\)
-
2.
\(v(\pi ^1) > v(\pi ^2)\)
-
3.
\(v(\pi ^1) < v(\pi ^2)\)
We will consider each of these three possibilities. Suppose \(v(\pi ^1) = v(\pi ^2)\) which implies that neither \(\pi ^1\) nor \(\pi ^2\) is the optimal sequence (due to the uniqueness assumption \(A_1\)). Since \(v(\pi ^1) = v(\pi ^2)\), the consequent of (Equation 7) becomes false. By contrapositive, its antecedant must be false, i.e., have:
In the same way, we get:
(9) and (10) can both be true only for \(d(\pi ^{\textsc {opt}}, \pi ^1) = d(\pi ^{\textsc {opt}}, \pi ^2)\). But as per Theorem 3, no point is equidistant from \(\pi ^1\) and \(\pi ^2\) because \(\pi ^1\) and \(\pi ^2\) are distance one apart. Clearly, the relation \(v(\pi ^1) = v(\pi ^2)\) is impossible.
Next, suppose \(v(\pi ^1) > v(\pi ^2)\). By Lemma 4, we get:
and
Since \(v(\pi ^1) > v(\pi ^2)\), the consequent of the implication in (12) is false. By contrapositive, its antecedant must be false, i.e., player 2 cannot belong to \(C^{\textsc {opt}}_2\). So he must belong to \(C^{\textsc {opt}}_1\) and we get:
Next, suppose \(v(\pi ^1) < v(\pi ^2)\). Then the consequent of the implication in (11) is false. By contrapositive, its antecedant must be false, i.e., player 2 cannot belong to \(C^{\textsc {opt}}_1\). So he must belong to \(C^{\textsc {opt}}_2\):
It takes \({\mathcal {O}}(n)\) time to assign to \(\pi ^1\) the sequence comprised of n singletons and to \(\pi ^2\) the sequence comprised of the grand coalition. So the position of player 2 can be found in \({\mathcal {O}}(n)\) time. Observe that to find this position, it is enough to know the relation between the values of \(\pi ^1\) and \(\pi ^2\) (i.e., whether \(v(\pi ^1) < v(\pi ^2)\) or \(v(\pi ^1) > v(\pi ^2)\)), but their actual values are not required. At this stage, we know the positions of players 1 and 2 in \(\pi ^{\textsc {opt}}\).
The positions of players\(3 \le i \le n\): In general, the position of player \(3 \le i \le n\) in \(\pi ^{\textsc {opt}}\) must be found given the positions of each of the players \(1, \ldots , i-1\). If m is such that at least one of the first \(i-1\) players belongs to \(C^{\textsc {opt}}_m\) but none of them belong to any of \(\{C^{\textsc {opt}}_{m+1}, C^{\textsc {opt}}_{m+2}, \ldots \}\), by Lemma 4, player i must belong to a unique coalition in the set \(\{C^{\textsc {opt}}_1, \ldots , C^{\textsc {opt}}_{m+1}\}\). This coalition is determined as follows. For each \(1 \le p \le m+1\), choose an instance \(\pi ^p = (C^p_1, C^p_2, \ldots )\) such that players 1 to \(i-1\) are in their respective optimal positions, player i is in coalition \(C^p_p\), and players \(i+1\) to n are singletons. Between the instances \(\pi ^1, \ldots \pi ^{m+1}\), call the one with the highest value \(\pi ^{max}\). Since \(1 \le max \le m+1\), we will consider each one of the \(m+1\) possibilities.
If \(max=1\), then for each \(\pi ^p\) where \(p \ne max\), \(v(\pi ^p) > v(\pi ^j)\) will be false. That is, the consequent of the implication (8) will be false and by contrapositive, its antecedant must be false, i.e., player i cannot belong to any coalition \(C^{\textsc {opt}}_p\) where \(p \ne max\). Thus, \(i \in C^{\textsc {opt}}_{max}\). We have now determined the coalition in \(\pi ^{\textsc {opt}}\) to which player i belongs.
For each \(3 \le i \le n\) and each \(1 \le p \le m+1\), it takes \({\mathcal {O}}(n)\) time to assign a sequence to \(\pi ^p\). A sequence can be assigned to all \(\pi ^1, \ldots , \pi ^{m+1}\) in \({\mathcal {O}}(n^2)\) time, after which max can be found in \({\mathcal {O}}(n)\) time. The position of all the n players can therefore be determined in \({\mathcal {O}}(n^3)\).
Observe that, for each \(3 \le i \le n\), it is enough to know the relation (> or <) between the values of coalition structures, their actual values are not required. \(\square \)
Algorithm 1, based on Theorem 4, is a greedy method for finding the optimal sequence \(\pi ^{\textsc {opt}} = (C^{\textsc {opt}}_1, C^{\textsc {opt}}_2, \ldots )\). In this method, the coalition in \(\pi ^{\textsc {opt}}\) to which player 1 belongs is determined first. Then, the positions of the remaining players are determined one by one: the position of player \(2 \le i \le n\) is determined on the basis of the positions of players \(1, \ldots , i-1\).

In more detail, Line 2 of Algorithm 1 assigns player 1 to the first coalition \(C^{\textsc {opt}}_1\). The for loop in Line 3 finds the coalition in \(\pi ^{\textsc {opt}}\) to which each of the players \(2 \le i \le n\) belongs. The steps within this loop are repeated \(n-1\) times; in iteration \(2 \le i \le n\), the coalition in \(\pi ^{\textsc {opt}}\) to which player i belongs is greedily determined as follows. Suppose that at least one of the first \(i-1\) players belongs to \(C^{\textsc {opt}}_m\) but none of them belong to any of the coalitions \(C^{\textsc {opt}}_{m+1}, C^{\textsc {opt}}_{m+2}, \ldots \). In each iteration of the for loop of Line 5, the sequence \(\pi ^p = \{C^p_1, C^p_2, \cdots \}\) is such that the first \(i-1\) players are in their respective optimal positions, player i is in \(C^p_p\) and players \(i+1\) to n are singletons. Thus these \(m+1\) structures differ only in the position of one player. Between the instances \(\pi ^1, \ldots \pi ^{m+1}\), call the one with the highest value \(\pi ^{max}\) (this is Line 6 of Algorithm 1). Then player i must belong to the coalition \(C^{\textsc {opt}}_{max}\) (this is Line 7 of Algorithm 1).
Line 1 takes \({\mathcal {O}}(n)\) time, Line 2 \({\mathcal {O}}(1)\), and Line 4 \({\mathcal {O}}(n)\). Lines 4 to 7 together take \({\mathcal {O}}(n)\) time. Since the for loop of Line 3 is repeated \(n-1\) times, the overall time complexity of Algorithm 1 is \({\mathcal {O}}(n^2)\).
Example 8 illustrates the operation of Algorithm 1.
Example 8
Suppose the set of players is \(N=\{1, 2, 3, 4\}\). There are 15 possible sequences and their values are as listed in Table 5. The optimum is \(\pi ^{\textsc {opt}}=(\{1,3\} \{2,4\})\). Player 1 must belong to the first coalition in \(\pi ^{\textsc {OPT}}\). Given this, the optimal position for player 2 must be either the first or the second coalition. Figure 2a lists all those partitions in which the players 1 and 2 are apart and Fig. 2b lists all those partitions in which they are together. If the optimal position for player 2 is the first (second) coalition, then per monotonicity, the value of each partition in Fig. 2a will be less (greater) than the value of each partition in Fig. 2b. Thus to determine the optimal position for player 2, it is enough to compare any one partition in Fig. 2a with any one in Fig. 2b. Compare the values of the partition \(\pi ^1\) comprised of all singletons with the partition \(\pi ^2\) comprised only of the grand coalition. Since \(v(\pi ^1) = 6\) and \(v(\pi ^2) = 2\), the optimal position for player 2 must be the second coalition. At this stage, we know that \(1 \in C^{\textsc {opt}}_1\) and \(2 \in C^{\textsc {opt}}_2\).
Given that the players 1 and 2 belong to different coalitions, the optimal position for player 3 must be one of the first three coalitions. Figure 3a lists all those partitions in which the player 3 belongs to the first coalition, Fig. 3b those partitions in which the player 3 belongs to the second coalition, and Fig. 3c those partitions in which the player 3 belongs to the third coalition. Consider partition \(\pi ^1=(\{1, 3\} \{2\} \{4\})\) of block (a), \(\pi ^2=(\{1\} \{2, 3\} \{4\})\) of block (b) and \(\pi ^3=(\{1\} \{2\} \{3, 4\})\) of block (c). Between these three, the one with highest value is \(v(\pi ^1)=9\) so player 3 must belong to the first coalition. At this stage, we know that \(1 \in C^{\textsc {opt}}_1\), \(2 \in C^{\textsc {opt}}_2\), and \(3 \in C^{\textsc {opt}}_1\).
The optimal position for player 4 must be one of the first three coalitions, so \(\pi ^{\textsc {opt}}\) must be one of the partitions \((\{1, 3, 4\} \{2\})\), \((\{1, 3\} \{2, 4\})\), or \((\{1, 3\} \{2\} \{4\})\). The optimum is \(\pi ^{\textsc {opt}} = (\{1, 3\} \{2, 4\})\) because, between the three possibilities, it has the highest value. Thus with five comparisons (one comparison to find the optimal position for player 2, two each to find the optimal position for players 3 and 4), we found the optimal partition.
5 Multiple optima, monotonic values, and a known player ordering
For a known player ordering, we will allow multiple optima. \(\varPi ^{\textsc {OPT}}\) will denote the setFootnote 5 of all optimal sequences. The monotonicity assumption is now defined as follows:
\({\bar{A}}_2\)Monotonicity: The function \(v: \varPi _N \rightarrow \mathbb {R}\) is monotonically decreasing in the distance of a sequence from each optimum, i.e., the following implication must be true:

As a consequence of the monotonicity assumption, the elements that comprise \(\varPi ^{\textsc {OPT}}\) are restricted to those partitions that are a certain distance apart. This is proven in Theorem 5.
Theorem 5
If the value function v is monotonic, then any two optima are distance \(1/(n-1)\) apart, i.e., the following implication must be true:

Proof
By contradiction. As per Theorem 1, we have \(1 \le \varDelta (\pi ^1, \pi ^2) \le n-1\). Assume that \(\varDelta (\pi ^1, \pi ^2)= 1 \le k \le n-2\). Let \(SF^1\) denote a sequence form for \(\pi ^1\) and \(SF^2\) that for \(\pi ^2\). Consider two arbitrary points \(SF^1_{k+1} \models \pi ^3\) and \(SF^2_{k+1} \models \pi ^4\) such that \(\pi ^3 \notin \varPi ^{\textsc {OPT}}\) and \(\pi ^4 \notin \varPi ^{\textsc {OPT}}\). Then we have:
With respect to the optimum \(\pi ^1\), the monotonicity assumption of (13) requires that
because \(d(\pi ^1, \pi ^3) <d(\pi ^1, \pi ^4)\) [as per (15) and (16)]. However, with respect to the optimum \(\pi ^2\), the monotonicity assumption of (13) requires that
because \(d(\pi ^2, \pi ^3) >d(\pi ^2, \pi ^4)\) [as per (17) and (18)]. (19) and (20) are contradictory. So the assumption that \(\varDelta (\pi ^1, \pi ^2)= 1 \le k \le n-2\) must be false and its negation, i.e., \(\varDelta (\pi ^1, \pi ^2) >n-2\), must be true. As per Theorem 1, \(1 \le \varDelta (\pi ^1, \pi ^2) \le n-1\), so we get \(\varDelta (\pi ^1, \pi ^2) = n-1\), i.e., \(d(\pi ^1, \pi ^2) = 1/(n-1)\). \(\square \)
Intuitively, Theorem 5 means that any two sequences in \(\varPi ^{\textsc {OPT}}\) can differ only with respect to the position of player n. In other words, the position, in any optimal sequence, of each player \(1 \ldots , n-1\) is unique. For example, for \(n=4\), it is possible for the sequences \((\{1,2\} \{3\} \{4\})\) and \((\{1,2\} \{3,4\})\) to belong to \(\varPi ^{\textsc {OPT}}\) because the distance between them is \(1/(n-1)\) and they differ only in terms of the position of player 4. However, if \((\{1,2\} \{3\} \{4\})\) is in \(\varPi ^{\textsc {OPT}}\) then \((\{1\} \{2, 3\} \{4\})\) cannot be in \(\varPi ^{\textsc {OPT}}\) because \(d((\{1,2\} \{3\} \{4\}), (\{1\} \{2, 3\} \{4\})) \ne 1/(n-1)\). The uniqueness of the positions of players \(1, \ldots , n-1\) is formalized in Lemma 5.
Let \(\beta ^i_{\pi }\) denote the index of the coalition in \(\pi \) to which player i belongs. In Lemma 5, we show that, for a \(\pi \in \varPi ^{OPT}\), \(\beta ^i_{\pi }\) is unique for each \(1 \le i < n\).
Lemma 5
In any optimal sequence \(\pi \in \varPi ^{\textsc {OPT}}\), there must be a unique coalition to which each player \(1 \le i < n\) belongs.
Proof
The proof is by contradiction. Consider a partition \(\pi ^1 \in \varPi ^{\textsc {OPT}}\), and another partition \(\pi ^2 \in \varPi ^{\textsc {OPT}}\). Consider any i (where \(1 \le i < n\)), and let player i belong to the coalition \(C^1_r\) in \(\pi ^1\) and the coalition \(C^2_s\) in \(\pi ^2\). Assume that \(r \ne s\). Without any loss of generality, suppose that \(r<s\). As per the definition of \(\varDelta \) given in (4), this supposition entails the following relation:
In the statement of the lemma, we are given that \(1 \le i < n\). Thus, (21) can also be written as
But by Theorem 5, \(d(\pi ^1, \pi ^2) = 1/(n-1)\). Equivalently, we have the following relation:
But (23) contradicts (22), so the assumption that \(r \ne s\) must be false. So its negation must be true, i.e., in any optimal sequence, there must be a unique coalition to which player \(1 \le i < n-1\) belongs. \(\square \)
From Theorem 5, it also follows that each point that is not a member of \(\varPi ^{\textsc {OPT}}\) is equidistant from each point in \(\varPi ^{\textsc {OPT}}\) (see Lemma 6 for proof).
Lemma 6
If the value function v is monotonic, then each point that is not a member of \(\varPi ^{\textsc {OPT}}\) must be equidistant from each point in \(\varPi ^{\textsc {OPT}}\), i.e., the following implication must be true:

Proof
From Theorem 5 we have \(\varDelta (\pi ^1, \pi ^2) = n-1\). Assume that \(\varDelta (\pi ^1, \pi ^3)=1 \le k \le n-1\). The two facts \(\varDelta (\pi ^1, \pi ^2) = n-1\) and \(\varDelta (\pi ^1, \pi ^3)=k\) together imply \(\varDelta (\pi ^2, \pi ^3)=k\). The partition \(\pi ^3\) is therefore equidistant from \(\pi ^1\) and \(\pi ^2\). \(\square \)
The above analysis leads to the following key insight. The setting with multiple optima differs from the one with a unique optimum in terms of the uniqueness of the coalition to which a player belongs. If the optimum is unique, each of the n players must belong to a unique coalition in \(\pi ^{\textsc {OPT}}\) (see Lemma 4). For multiple optima, each of the players \(1, \ldots , n-1\) must belong to a unique coalition in any optimum but the position of player n may differ from one optimum to another (see Lemma 5). Lemma 7 is a formalization of this insight and it is the multiple optima analog of Lemma 4.
Lemma 7
Suppose the coalition in \(\pi ^{\textsc {opt}}=(C^{\textsc {opt}}_1, C^{\textsc {opt}}_2, \ldots )\) to which each of the the players in \(\{1, \ldots , 1 \le i-1 \le n-2\}\) belongs is known. Let m be such that at least one of the first \(i-1\) players belongs to \(C^{\textsc {opt}}_m\) but none of them belong to any of the coalitions \(C^{\textsc {opt}}_{m+1}, C^{\textsc {opt}}_{m+2}, \ldots \). Then, player i must belong to a unique coalition \(C^{\textsc {opt}}_p\) where \(C^{\textsc {opt}}_p \in \{C^{\textsc {opt}}_1, \ldots , C^{\textsc {opt}}_{m+1}\}\). Further, for two arbitrary sequence forms \(SF^1_i(k)\) and \(SF^2_i(k)\) such that \(SF^1_i(k) = SF^{\textsc {OPT}}_i(k)\) for \(1 \le k \le i\) and \(SF^2_i(k) = SF^{\textsc {OPT}}_i(k)\) for \(1 \le k \le i-1\) and \(SF^2_i(i) \ne SF^{\textsc {OPT}}_i(i)\), and two arbitrary sequences \(\pi ^1 = (C^1_1, C^1_2, \ldots )\) and \(\pi ^2 = (C^2_1, C^2_2, \ldots )\) such that \(\pi ^1 \models SF^1_i\) and \(\pi ^2 \models SF^2_i\), the following implication must be true:
Proof
As Lemma 4. \(\square \)
Observe that the difference between Lemma 4 and Lemma 7 is that the former draws inferences about the position of any player \(1 \le i \le n\) given the positions of all the palyers \(1, \ldots , i-1\), while the latter draws inferences about the position of any player \(1 \le i \le n-1\) given the positions of all the players \(1, \ldots , i-1\). We are now ready to present the main result of this section. Theorem 6 is a constructive proof of polynomial time complexity of computing optima.
Theorem 6
If there are multiple optima and the value function is monotonic, all the optimal sequences in \(\varPi ^{\textsc {opt}}\) can be determined in \({\mathcal {O}}(n^2)\) time.
Proof
For multiple optima, there is a unique coalition to which each player except player n belongs in any optimum (see Lemma 5). For a unique optimum, there is a unique coalition to which each of the n players belongs (see Lemma 4). Given this, the optimal positions of players \(1, \ldots , n-1\) for multiple optima can be determined in \({\mathcal {O}}(n^2)\) time as was done in the proof of Theorem 4.
Let m be such that at least one of the first \(n-1\) players belongs to \(C^{\textsc {opt}}_m\) but none of them belongs to any of the coalitions \(C^{\textsc {opt}}_{m+1}, C^{\textsc {opt}}_{m+2}, \ldots \). By fixing the positions of these \(n-1\) players, it is possible to generate \(m+1\) different sequences of n players. If \(\varPi ^{\textsc {POS}}\) denotes the set of these \(m+1\) sequences then \(\varPi ^{\textsc {OPT}} \subseteq \varPi ^{\textsc {POS}}\). By searching the set \(\varPi ^{\textsc {POS}}\), the set of all optima be found in \({\mathcal {O}}(n)\) time.
The total time required to find all the optimal sequences is \({\mathcal {O}}(n^2)\) which is the sum of the time taken to find the optimal position of each of the players \(1, \ldots , n-1\) (i.e., \({\mathcal {O}}(n^2)\)) and the time to find the optimal positions of player n (i.e., \({\mathcal {O}}(n)\)). As in Theorem 4, information is required only about the relation (> or <) between the values of partitions but not their actual values. \(\square \)

Algorithm 2 is an extension of Algorithm 1, and Theorem 6 is proof of correctness of this algorithm. As far as Line 9, Algorithm 2 is the same as Algorithm 1, except for the index of the for loop of Line 3. By the end of the for loop of Line 3, the optimal positions of the first \(n-1\) players will have been determined by Algorithm 2. Lines 10 to 12 are for determining the set \({\mathbb {S}}^{\textsc {opt}}\) of optimal structures. The \(m+1\) sequences, \(\pi ^1, \ldots , \pi ^{m+1}\), form the superset of \({\mathbb {S}}^{\textsc {opt}}\), and this superset is then searched to find \({\mathbb {S}}^{\textsc {opt}}\).
Now consider the time complexity of Algorithm 2. We already know (from the analysis of Algorithm 1) that Lines 1 to 9 take \({\mathcal {O}}(n^2)\) time. Lines 10 to 12 require \({\mathcal {O}}(n)\) time. The time complexity of Algorithm 2 is therefore \({\mathcal {O}}(n^2)\).
6 Multiple optima, quasi-monotonic values, and a known player ordering
For a known ordering, we allow multiple optima and relax the monotonicity assumption. As before, \(\varPi ^{\textsc {OPT}}\) denotes the set of all optima. Let \(q_{max}\) and \(q_{min}\) be defined as follows:
In words, \(q_{min}\) (\(q_{max}\)) is the the minimum (maximum) \(\varDelta \) for any two optimal sequences. Observe that \({\mathcal {D}}(\varPi ^{\textsc {OPT}}) = 1/q_{min}\).
For this setting, the value function v need be monotonic only for a subset of \(\varPi _N\). Let \(\varPi ^{\textsc {MON}}\) denote the set of all those non-optimal points that are more distant than the diameter of \(\varPi ^{\textsc {OPT}}\) from each point in \(\varPi ^{\textsc {OPT}}\). Then a function v is quasi-monotonic if the set of points in \(\varPi ^{\textsc {MON}}\) satisfy monotonicity. Formally, quasi-monotonicity is stated as follows:
\(\bar{{\bar{A}}}_2\)Quasi-monotonicity: The function \(v: \varPi ^{\textsc {MON}} \rightarrow \mathbb {R}\) is monotonically decreasing in the distance of a sequence from each optimum, i.e., the following implication must be true:

In order to give an indication of the size of search space for which v is monotonic relative to the size of the space for which it is not, we introduce the terms ‘degree of monotonicity’, and ‘degree of non-monotonicity’, of v.
Definition 6
For multiple optima and a quasi-monotonic v, the degree of monotonicity is \(q_{min}\) and the degree of non-monotonicity is \(n - q_{min}\).
Observe that the degree of monotonicity (non-monotonicity) is increasing (decreasing) in \(q_{min}\). Lemmas 8 and 9 establish preliminary results which we use to build the main result on time complexity in Theorem 7.
Lemma 8
If the value function v is quasi-monotonic then each point in the set \(\varPi ^{\textsc {MON}}\) must be equidistant from each point in \(\varPi ^{\textsc {OPT}}\), i.e., we have the implication:

Proof
The proof is by contradiction. Consider any three points \(\pi ^1 \in \varPi ^{\textsc {MON}}\)\(\pi ^2 \in \varPi ^{\textsc {OPT}}\), and \(\pi ^3 \in \varPi ^{\textsc {OPT}}\). Given that the diameter of \(\varPi ^{\textsc {OPT}}\) is \(1/q_{min}\), we get \(d(\pi ^2, \pi ^3) \le 1/q_{min}\). Equivalently, \(\varDelta (\pi ^2, \pi ^3) \ge q_{min}\), and we get:
As per the definition of \(\varPi ^{\textsc {MON}}\), \(d(\pi ^1, \pi ^2) > 1/q_{min}\) and \(d(\pi ^1, \pi ^3) > 1/q_{min}\). Equivalently, \(\varDelta (\pi ^1, \pi ^2) < q_{min}\) and \(\varDelta (\pi ^1, \pi ^3) < q_{min}\). Denote \(\varDelta (\pi ^1, \pi ^2)\) as r and \(\varDelta (\pi ^1, \pi ^3)\) as s. Assume that \(r \ne s\). Without any loss of generality, suppose that \(r < s\) where \(s < q_{min}\). Then the player \(r+1\) must belong to different coalitions in \(\pi ^1\) and \(\pi ^2\), i.e.,
However, because \(r<s\) and \(\varDelta (\pi ^1, \pi ^3) = s\), we get:
(26) and (27) entail the following inequality:
Since \(r< s < q_{min}\), we get \(r+1 < q_{min}\). Since \(r+1 < q_{min}\), (28) contradicts (25). This renders the assumption \(r \ne s\) false. So each point in the set \(\varPi ^{\textsc {MON}}\) must be equidistant from each point in \(\varPi ^{\textsc {OPT}}\). \(\square \)
Lemma 9
In any optimal sequence \(\pi \in \varPi ^{\textsc {OPT}}\), there must be a unique coalition to which each player \(1 \le i \le q_{min}\) belongs.
Proof
The proof is by contradiction. Consider a partition \(\pi ^1 \in \varPi ^{\textsc {OPT}}\), and another partition \(\pi ^2 \in \varPi ^{\textsc {OPT}}\). Let player \(1 \le i \le q_{min}\) belong to the coalition \(C^1_r\) in \(\pi ^1\) and the coalition \(C^2_s\) in \(\pi ^2\). Assume that \(r \ne s\). Without any loss of generality, suppose that \(r<s\). As per the definition of \(\varDelta \) given in (4), this supposition entails the following relation:
As per the coalition ordering principle given in Sect. 2, in any partition, player i must belong to any one of the first i coalitions, i.e., \(r < s \le i\). Since \(i \le q_{min}\), we can write (29) as follows:
But we are given that the diameter of \(\varPi ^{\textsc {OPT}}\) is \(1/q_{min}\). Equivalently, we have the following relation:
Clearly, (31) and (30) are contradictory. The assumption that \(r \ne s\) must be false and its negation must be true, i.e., in any optimal sequence, there must be a unique coalition to which player \(1 \le i < q_{min}\) belongs. \(\square \)
Theorem 7
If there are multiple optima and value function is quasi-monotonic, an optimal sequence can be determined in \({\mathcal {O}}(n^2) + {\mathcal {O}}(n^{n-q_{min}})\) time.
Proof
As per Lemma 9, each player \(1 \le i \le q_{min}\) must belong to a unique coalition in any optimal partition. Thus the position of each of the players \(1, \ldots , q_{min}\) can be determined as in the proof of Theorem 4 in \({\mathcal {O}}(n^2)\) time.
The sequence form in which the position of each of the players \(1, \ldots , q_{min}\) is fixed to their respective optimal positions, gives rise to \({\mathcal {O}}(n^{n-q_{min}})\) instances. A brute force search on these \({\mathcal {O}}(n^{n-q_{min}})\) partitions will yield an optimal partition.
Since it takes \({\mathcal {O}}(n^2)\) time to find the optimal positions of the players \(1, \ldots , q_{min}\) and \({\mathcal {O}}(n^{n-q_{min}})\) time for exhaustively searching the space of remaining possible partitions, the total search time will be \({\mathcal {O}}(n^2) + {\mathcal {O}}(n^{n-q_{min}})\). \(\square \)
It is now evident that the search time is least for \(n-1 \le q_{min} \le n-3\) as the optimal positions of the players \(1, \ldots , n-4\) can be found in \({\mathcal {O}}(n^2)\) time and the non-monotonic part can also be searched in \({\mathcal {O}}(n^2)\) resulting in an overall polynomial time complexity of \({\mathcal {O}}(n^2)\). As the degree of non-monotonicity increases, the time complexity successively worsens becoming increasingly exponential and reaching the extreme of \({\mathcal {O}}(n^{n-1})\) for \(q_{min}=1\) which corresponds to the entire search space being non-monotonic.
The search method is formulated in Algorithm 3. Algorithm 3 is similar to Algorithm 2 in finding the coalition to which player \(1 \le i \le q_{min}\) belongs. Thereafter, the search space is comprised of all possible instances of \(SF_{q_{min}}\) and this must be searched to find an optimum. The time to find an optimum by using brute force over the space of possible instances of \(SF_{q_{min}}\) is \({\mathcal {O}}(n^{n-q_{min}})\).

In summary, a quasi-monotonic space of all possible partitions is searched in the following two stages:
-
1.
First, for the monotonic part, run Algorithm 3 to obtain an optimal sequence form \(SF_{q_{min}}\).
-
2.
Next, use brute force to search only the instances of \(SF_{q_{min}}\).
Observe that none of the proposed greedy methods (viz., Algorithm 1, Algorithm 2, or Algorithm 3) needs numeric values of coalition structures. Only an ordering on the values is needed.
7 Unique optimum, monotonic values, and an unknown player ordering
So far, we considered games with a known player ordering. Now we will consider a setting in which a player ordering is known to exist but the ordering itself is unknown. We still have the assumptions \(A_1\) (i.e., a unique optimal sequence) and \(A_2\) (monotonicity) defined in Sect. 3.1. In more detail, it is known that the ith priority player \(P_i\) is a unique element of the set N but it is not known which element of N it is. For this setting, we prove in Sect. 7.1 that the optimal coalition structure determination problem is solvable in polynomial time and devise such an algorithm. Then, in Sect. 7.2, we illustrate the working of this algorithm for 3-player games.
7.1 n-Player games
In this setting, the identities of the players \(P_1, \ldots , P_n\) and their optimal coalitions are unknown. All we know is that the identity of each \(P_i\) and its optimal coalition is unique. For this, we will first informally outline the key steps of our method for finding the optimal sequence and then proceed to formal constructive proofs in Theorems 8 to 10 and Lemmas 10 to 19. A detailed formulation of the method is in Algorithms 4 and 5.
At a high level, our method for determining the optimal sequence is comprised of two key steps:
-
Step 1
Determine who the two top priority players are, and their optimal coalitions.
-
Step 2
For \(3 \le i \le n\), determine the identity of the player \(P_i\) and its optimal coalition.
Consider Step 1 first. To begin, we know that \(P_1 \in N\), so there are n possibilities for the identity of \(P_1\). We also know that its optimal coalition must be \(C^{OPT}_1\). Then, for any one possibility for \(P_1\), say \(P_1=x\), we know that there must be \(n-1\) possibilities for the identity of \(P_2\), i.e., \(P_2 \in N - \{x\}\), and that there must be two possibilities for its optimal coalition, i.e., \(P_2\) must be a member of either \(C^{OPT}_1\) or \(C^{OPT}_2\). Let Z be the set of all these possibilities and let each element of Z be a quadruple defined as follows:
The semantics of a quadruple is that the first element is the identity of player \(P_1\), the second element is the identity of \(P_2\), the third element is x’s optimal coalition (i.e., \(x \in C^{OPT}_1\)), and the last element is y’s optimal coalition (i.e., \(y \in C^{OPT}_z\)). For example, the quadruple (2, 3, 1, 2) means that \(P_1=2\), \(P_2=3\), \(2 \in C^{OPT}_1\), and \(3 \in C^{OPT}_2\).
We find it convenient to introduce terminology for referring to certain pairs of elements of Z.
Definition 7
For any \(x \in N\) and any \(y \in N - \{x\}\), (x, y, 1, 1) and (y, x, 1, 1) are each others’ partners, and (x, y, 1, 2) and (y, x, 1, 2) are each others’ partners. A partner pair is in one of the following forms:
-
((x, y, 1, 1), (y, x, 1, 1))
-
((x, y, 1, 2), (y, x, 1, 2))
Lemma 10 readily follows from the definition of Z and that of a partner pair.
Lemma 10
The set Z satisfies the following assertions:
-
\(|Z| = 2 \times n \times (n-1)\).
-
Every element in Z has a unique partner in Z.
-
Every element in Z is the partner of a unique element in Z.
For monotonic value functions, each one of the possibilities in Z induces a relation between the values of certain structures. For instance, consider the element (1, 2, 1, 1) of Z. The semantics of (1, 2, 1, 1) is that \(P_1=1\), \(P_2 = 2\), \(1 \in C^{OPT}_1\), and \(2 \in C^{OPT}_1\). For this specific possibility, monotonicity induces the following implication:

In words, if \((P_1= 1 \wedge P_2 = 2 \wedge 1 \in C^{OPT}_1 \wedge 2 \in C^{OPT}_1)\), then every structure \(\pi ^1\) in which the players 1 and 2 are in the same coalition must have a higher value than every structure \(\pi ^2\) in which they are in different coalitions. In general, for the quadruple (i, j, 1, 1), monotonicity induces the implication labelled \(X_1\) in Table 6. In the same way, for the quadruple (i, j, 1, 2), monotonicity induces the implication \(X_2\) in Table 6.
Now, consider the possibility that \((P_1= 1 \wedge P_2 = 2 \wedge 1 \in C^{OPT}_1 \wedge 2 \in C^{OPT}_1)\), i.e., for \(i=1\) and \(j=2\), the antecedant of the implication \(X_1\) is true. This means that the consequent of \(\overset{L}{\Rightarrow }\) must be true. However, if we can find some \(\pi ^1\) and \(\pi ^2\) such that \((\beta ^1_{\pi ^1} = \beta ^2_{\pi ^1}) \wedge (\beta ^1_{\pi ^2} \ne \beta ^2_{\pi ^2})\) and \(v(\pi ^1) \le v(\pi ^2)\), then the antecedant of \(\overset{R}{\Rightarrow }\) will be be true but its consequent will be false. So the consequent of \(\overset{L}{\Rightarrow }\) will be false, and by contrapositive, its antecedant must be false. This means we can eliminate the possibility that \((P_1= 1 \wedge P_2 = 2 \wedge 1 \in C^{OPT}_1 \wedge 2 \in C^{OPT}_1)\). We use this idea to set up certain tests for comparing the values of certain structures in a way that will enable us to eliminate those possibilities from Z that are guaranteed not to correspond to the optimal structure.
We define two tests called T1 and T2 listed in Table 7. Each test compares the values of two partitions. The test T1 is a comparison of the values of the partition \(\pi ^G\) comprised of the single grand coalition and the partition \(\pi ^S\) comprised of all singletons. The test T2(i, j) is a comparison of the values of the partitions \((N - \{i\}, \{i\})\) and \((N - \{j\}, \{j\})\) where i and j are any two distinct players. Each of these tests will result in one of three possible outcomes: <, \(=\), or >. Depending on the resulting outcome, certain deductions can be made about who the two top priority players are and whether they belong to the same or to different coalitions in \(\pi ^{OPT}\).
In more detail, the purpose of test T1 is to determine whether or not the two top priority players belong to the same coalition in \(\pi ^{OPT}\). The purpose of test T2 is to determine the identities of \(P_1\) and \(P_2\). This goal is achieved indirectly by a process of determining, one by one, each one of those players who are guaranteed to be neither \(P_1\) nor \(P_2\) and eliminating them from consideration.
Theorem 8 and Lemma 11 are a formalization of the eliminations that result from the outcomes of T1, and the deductions they entail. Theorem 9 and Lemmas 12 to 16 are a formalization of the eliminations that result from T2, and the deductions they entail.
In what follows, E will denote the set of those elements of Z that get eliminated as the result of a test. \({\overline{Z1}} \subset Z\) (\({\underline{Z1}} \subset Z\)) will denote the set of possibilities before (after) the test T1. \({\overline{Z2}} \subset Z\) (\({\underline{Z2}} \subset Z\)) will denote the set of possibilities before (after) the test T2(i, j).
Theorem 8
The test T1 defined in Table 7 will result in the following eliminations:
Proof
The test T1 compares \(v(\pi ^G)\) (the value of the coaliiton structure comprised of the single grand coalition) and \(v(\pi ^S)\) (the value of the coalition structure comprised of all singleton coalitions) and must result in one of the following three outcomes:

-
1.
\(v(\pi ^G) < v(\pi ^S):\) Consider the implication \(X_1\) defined in Table 6 and suppose \(\pi ^1=\pi ^G\) and \(\pi ^2=\pi ^S\). If \(v(\pi ^G) < v(\pi ^S)\), then for any two distinct players i and j, the antecedant of \(\overset{R}{\Rightarrow }\) will be true while its consequent will be false. This means that the consequent of \(\overset{L}{\Rightarrow }\) will be false, so, by contrapositive, its antecedant must be false. In other words, (i, j, 1, 1) and (j, i, 1, 1) are both impossible options for the two top priority players. So both (i, j, 1, 1) and (j, i, 1, 1) must be eliminated from Z. Since (i, j, 1, 1) and (j, i, 1, 1) are a pair, elements are eliminated in pairs.
-
2.
\(v(\pi ^G) > v(\pi ^S):\) Consider the implication \(X_2\) defined in Table 6 and suppose \(\pi ^1=\pi ^G\) and \(\pi ^2=\pi ^S\). If \(v(\pi ^G) > v(\pi ^S)\), then for any two distinct players i and j, the antecedant of \(\overset{R}{\Rightarrow }\) will be true while its consequent will be false. This means that the consequent of \(\overset{L}{\Rightarrow }\) will be false, so, by contrapositive, its antecedant must be false. In other words, (i, j, 1, 2) and (j, i, 1, 2) are both impossible options for the two top priority players. So (i, j, 1, 2) and (j, i, 1, 2) must both be eliminated from Z. Since (i, j, 1, 2) and (j, i, 1, 2) are a pair, elements are eliminated in pairs.
-
3.
\(v(\pi ^G) = v(\pi ^S):\) Combining the above arguments for the two cases \(v(\pi ^G) < v(\pi ^S)\) and \(v(\pi ^G) > v(\pi ^S)\), (i, j, 1, 1), (j, i, 1, 1), (i, j, 1, 2), and (j, i, 1, 2) must all be eliminated from Z leaving Z empty. As we will prove in Lemma 15, an empty Z marks a violation of monotonicity.\(\square \)
Lemma 11
For the test T1:
-
1.
If \(v(\pi ^G) < v(\pi ^S)\), then all the assertions in first column of Table 8 will be valid.
-
2.
If \(v(\pi ^G) > v(\pi ^S)\), then all the assertions in second column of Table 8 will be valid.
-
3.
If \(v(\pi ^G) = v(\pi ^S)\), then \({\underline{Z1}} = \{\}\)Footnote 6
Proof
The assertions in the first three rows of Table 8 follow readily from Theorem 8.
As per Lemma 10, every element in Z has a unique partner in Z, and is the partner of a unique element in Z. Then, as per Theorem 8, T1 only eliminates elements in pairs. The assertions in the last two rows of Table 8 follow. \(\square \)
It should now be evident that the test T1 is useful for determining whether or not the two top priority players belong to the same coalition in \(\pi ^{OPT}\). If \(v(\pi ^G) < v(\pi ^S)\), then \(P_1\) and \(P_2\) belong to different coalitions in \(\pi ^{OPT}\). On the other hand, if \(v(\pi ^G) > v(\pi ^S)\), then \(P_1 \in C^{OPT}_1\) and \(P_2 \in C^{OPT}_1\). However, the identities of \(P_1\) and \(P_2\) are still unknown. The test T2 is for finding \(P_1\) and \(P_2\). T2 follows T1. Further, T2 is conducted repeatedly until the condition for termination (defined below) is satisfied. The following is a high-level overview of the whole process:

Theorem 9 and Lemmas 12 to 16 are a formalization of the eliminations that result from T2.
Theorem 9
Suppose that \(\pi ^1 = (N-\{i\}, \{i\})\) and \(\pi ^2 = (N-\{j\}, \{j\})\) for any two distinct players i and j. The test T2 defined in Table 7 will result in the following eliminations:
where \(S_1\), \(S_2\), \(S_3\), and \(S_4\) are defined as follows.
Proof
The test T2 compares \(v((N - \{i\}, \{i\}))\) and \(v((\{N - j\}, \{j\}))\), so it must result in one of the following three outcomes.

-
1.
If \(v((N - \{i\}, \{i\})) < v((N - \{j\}, \{j\}))\), then for every (u, j, 1, 1) where \(u \ne i\) and \(u \ne j\), the antecedant of \(\overset{R}{\Rightarrow }\) in \(X_1\) (see Table 6) is true while the consequent is false. This means that the consequent of \(\overset{L}{\Rightarrow }\) will be false, and by contrapositive, its antecedant must be false. So (u, j, 1, 1) must be eliminated from Z. Likewise, (j, u, 1, 1) must also be eliminated. Observe that elements are eliminated in pairs. Then, for every (u, i, 1, 2) where \(u \ne i\) and \(u \ne j\), the antecedant of \(\overset{R}{\Rightarrow }\) in \(X_2\) (see Table 6) is true while the consequent is false. By contrapositive, the antecedant of \(\overset{L}{\Rightarrow }\) in \(X_2\) must be false. Thus (u, i, 1, 2) must be eliminated from Z. Likewise, (i, u, 1, 2) must also be eliminated. Again, elements are eliminated in pairs.
-
2.
If \(v((N - \{i\}, \{i\})) > v((N - \{j\}, \{j\}))\), then for every (u, j, 1, 2) where \(u \ne i\) and \(u \ne j\), the antecedant of \(\overset{R}{\Rightarrow }\) in \(X_2\) is true while the consequent is false. By contrapositive, the antecedant of \(\overset{L}{\Rightarrow }\) in \(X_2\) must be false. (u, j, 1, 2) must be eliminated from Z. Likewise, (j, u, 1, 2) must also be eliminated. Here too elements are eliminated in pairs. Then, for every (u, i, 1, 1) where \(u \ne i\) and \(u \ne j\), the antecedant of \(\overset{R}{\Rightarrow }\) in \(X_1\) is true while its consequent is false. By contrapositive, the antecedant of \(\overset{L}{\Rightarrow }\) in \(X_1\) must be false. Thus (u, i, 1, 1) must be eliminated from Z. Likewise, (i, u, 1, 1) must also be eliminated. Note again that elements are eliminated in pairs.
-
3.
If \(v((N - \{i\}, \{i\})) = v((N - \{j\}, \{j\}))\), then combine the arguments made above for \(v((N - \{i\}, \{i\})) < v((N - \{j\},\{j\}))\) and \(v((N - \{i\}, \{i\})) > v((N - \{j\},\{j\}))\) to get \(E = S_1 \cup S_2 \cup S_3 \cup S_4\). Here again that elements are eliminated in pairs.
\(\square \)
Lemma 12 establishes the relation between the sets \({\overline{Z2}}\) (i.e., the possibilities before T2) and \({\underline{Z2}}\) (i.e., the possibilities after T2).
Lemma 12
Suppose every element in \({\overline{Z2}}\) has a unique partner in \({\overline{Z2}}\), and every element in \({\overline{Z2}}\) is the partner of a unique element in \({\overline{Z2}}\). Then, regardless of the outcome of T2, every element in \({\underline{Z2}}\) must have a unique partner in \({\underline{Z2}}\), and every element in \({\underline{Z2}}\) must be the partner of a unique element in \({\underline{Z2}}\).
We are given that every element in \({\overline{Z2}}\) has a unique partner in \({\overline{Z2}}\), and every element in \({\overline{Z2}}\) is the partner of a unique element in \({\overline{Z2}}\). Now, the eliminations that result from T2 are defined in Theorem 9 in terms of the sets \(S_1\), \(S_2\), \(S_3\), and \(S_4\). The very definition of these four sets entails the following assertion:
For \(1 \le i \le 4\), each element in \(S_i\) has a unique partner in \(S_i\), and is the partner of a unique element in \(S_i\).
It follows that, regardless of the outcome of T2, every element in \({\underline{Z2}}\) must have a unique partner in \({\underline{Z2}}\), and every element in \({\underline{Z2}}\) must be the partner of a unique element in \({\underline{Z2}}\).
It should now be evident that by varying i and j, T2(i, j) can be used for eliminations. In Lemma 13, we prove that T2 can be used for eliminations as long as the set of possibilities for the two top priority players contains at least two partner pairs.
Lemma 13
If the set of possibilities for the two top priority players contains at least two partner pairs, T2 can be guaranteed to result in eliminations.
Proof
As per Definition 7, there are two possible forms for a partner pair, so any two pairs must be in one of the following forms.
-
\(\bigl ((i, x, 1, 1), (x, i, 1, 1)\bigr )\), \(\bigl ((j, x, 1, 1), (x, j, 1, 1)\bigr )\) where \(i \ne j\).
-
\(\bigl ((i, x, 1, 2), (x, i, 1, 2)\bigr )\), \(\bigl ((j, x, 1, 2), (x, j, 1, 2)\bigr )\) where \(i \ne j\).
-
\(\bigl ((i, x, 1, 1), (x, i, 1, 1)\bigr )\), \(\bigl ((j, x, 1, 2), (x, j, 1, 2)\bigr )\) where \(i \ne j\).
For any \(i \in N\) and \(j \in N - \{i\}\), consider any \(x \in N\) such that \(x \ne i\) and \(x \ne j\). Suppose \({\overline{Z2}}\) contains the pairs ((i, x, 1, 1), (x, i, 1, 1)) and ((j, x, 1, 1), (x, j, 1, 1)). As per Theorem 9, if the outcome of T2(i, j) is \(v(\pi ^1) \le v(\pi ^2)\) where \(\pi ^1 = (N - \{i\}, \{i\})\) and \(\pi ^2 = (N - \{j\}, \{j\})\), then the pair ((j, x, 1, 1), (x, j, 1, 1)) must be eliminated. On the other hand, if the outcome of T2(i, j) is \(v(\pi ^1) \ge v(\pi ^2)\), then the pair ((i, x, 1, 1), (x, i, 1, 1)) must be eliminated. Regardless of the outcome of T2(i, j), eliminations are guaranteed.
Next, suppose \({\overline{Z2}}\) contains ((i, x, 1, 2), (x, i, 1, 2)) and ((j, x, 1, 2), (x, j, 1, 2)). As per Theorem 9, if the outcome of T2(i, j) is \(v(\pi ^1) \le v(\pi ^2)\) where \(\pi ^1 = (N - \{i\}, \{i\})\) and \(\pi ^2 = (N - \{j\}, \{j\})\), then the pair ((i, x, 1, 2), (x, i, 1, 2)) must be eliminated. On the other hand, if the outcome of T2(i, j) is \(v(\pi ^1) \ge v(\pi ^2)\), then the pair ((j, x, 1, 2), (x, j, 1, 2)) must be eliminated. Regardless of the outcome of T2(i, j), eliminations are guaranteed.
Consider the last case where \({\overline{Z2}}\) contains the pairs ((i, x, 1, 1), (x, i, 1, 1)) and ((j, x, 1, 2), (x, j, 1, 2)). However, as per Lemma 12, such a situation can never arise since T1 is done before T2. At the end of T1, it will be known whether the two top priority players belong to the same or to different coalitions in \(\pi ^{OPT}\). \(\square \)
Lemma 14
If the set of possibilities for the two top priority players contains only one partner pair, then T2 cannot be guaranteed to result in eliminations.
Proof
As per Theorem 9, the only eliminations possible from T2(i, j) for any \(i \in N\) and \(j \in N - \{i\}\) are \(S_1\), \(S_2\), \(S_3\), and \(S_4\). We are given that the set of possibilities for the two top priority players, \({\overline{Z2}}\), contains only one partner pair. From the definition of partner pair (see Definition 7) and the definitions of the sets \(S_1\), \(S_2\), \(S_3\), and \(S_4\) (see Theorem 9), it is evident that \({\overline{Z2}}\) can be a subset of only one of the four sets \(S_1\), \(S_2\), \(S_3\), and \(S_4\). For elimination to occur, \({\overline{Z2}}\) must be a subset of one of the four sets \(S_1\), \(S_2\), \(S_3\), and \(S_4\).
As per Definition 7, a partner pair must be of the form ((x, y, 1, 1), (y, x, 1, 1)) or ((x, y, 1, 2), (y, x, 1, 2)) where \(x \in N\) and \(y \in N - \{i\}\). Suppose the pair in \({\overline{Z2}}\) is of the form ((x, y, 1, 1), (y, x, 1, 1)). Now, neither (x, y, 1, 1) nor (y, x, 1, 1) can belong to \(S_1\) or \(S_4\). (x, y, 1, 1) and (y, x, 1, 1) must both belong to \(S_2\) or both to \(S_3\). For the former case, elimination is possible only if \(v(\pi ^1) \le v(\pi ^2)\) where \(\pi ^1 = (N-\{i\}, \{i\})\) and \(\pi ^2 = (N-\{j\}, \{j\})\) but not if \(v(\pi ^1) > v(\pi ^2)\). For the latter, elimination is possible only if \(v(\pi ^1) \ge v(\pi ^2)\) but not if \(v(\pi ^1) < v(\pi ^2)\). In other words, elimination may or may not happen depending on the outcome of T2. Thus, T2(i, j) is not guaranteed to result in eliminations if the set of possibilities for the two top priority players contains only the pair ((x, y, 1, 1), (y, x, 1, 1)).
By the same argument, T2(i, j) is not guaranteed to result in eliminations if the pair in \({\overline{Z2}}\) is of the form ((x, y, 1, 2), (y, x, 1, 2)). \(\square \)
At this stage, we know from Lemma 13 those conditions under which T2 is guaranteed to result in eliminations, and from Lemma 14, those conditions under which T2 is not guaranteed to result in eliminations. This raises the question ‘can T2 result in the elimination of all possibilities so that \({\underline{Z2}} = \{\}\)?’. As we prove in Lemma 15, the elimination of all possibilities implies a violation of monotonicity.
Lemma 15
After eliminations from T2, if the set of possibilities that remain is empty, then monotonicity is violated.
Proof
The optimal structure is known to be unique and values monotonic. The basis of all the eliminations that result from T1 and T2 are the monotonicity induced implications \(X_1\) and \(X_2\) given in Table 6. Thus, if the set of possibilities that remain after eliminations becomes empty, monotonicity must have been violated.
We are now going to prove in Lemma 16 that T2, if done after T1, will reveal certain facts about the two top priority players.
Lemma 16
For arbitrary \(i \in N\) and \(j \in N - \{i\}\), the outcome of T2(i, j) will reveal the following facts:
-
1.
 if \(v(\pi ^1) \le v(\pi ^2)\)
if \(v(\pi ^1) \le v(\pi ^2)\) -
2.
 if \(v(\pi ^1) \ge v(\pi ^2)\)
if \(v(\pi ^1) \ge v(\pi ^2)\)
where \(\pi ^1 = (N - \{i\}, \{i\})\) and \(\pi ^2 = (N - \{j\}, \{j\})\).
Proof
Recall that T1 is done before any run of T2. As per Lemma 11, after T1, \({\underline{Z1}}\) must be in one of the following two forms:
-
1.
\({\underline{Z1}} = \{(x, y, 1, 2) | (x, y, 1, 2) \in Z\}\): If the outcome of T2(i, j) is \(v(\pi ^1) \le v(\pi ^2)\) then, as per Theorem 9, we have the following.
$$\begin{aligned} {\underline{Z2}}= & {} {\overline{Z2}} - (S_1 \cup S_2) \nonumber \\= & {} {\underline{Z1}} - (S_1 \cup S_2) \end{aligned}$$(32)with the sets \(S_1\) and \(S_2\) as defined therein. Since \(S_2 \not \subseteq {\underline{Z1}}\), we get
$$\begin{aligned} {\underline{Z2}}= & {} {\underline{Z1}} - S_1 \\= & {} \{(x, y, 1, 2) | (x, y, 1, 2) \in Z\} - \\&(\{(i, u,1,2) \ | \ u \ne i, u \ne j\} \ \cup \ \{(u, i, 1, 2) \ | \ u \ne i, u \ne j\}) \end{aligned}$$This clearly means that, if i is one of the two top priority players, the other one must be j. This is the first implication given in the statement of this Lemma.
On the other hand, if the outcome of T2(i, j) is \(v(\pi ^1) \ge v(\pi ^2)\) then, as per Theorem 9, we have the following.
$$\begin{aligned} {\underline{Z2}}= & {} {\overline{Z2}} - (S_3 \cup S_4) \nonumber \\= & {} {\underline{Z1}} - (S_3 \cup S_4) \end{aligned}$$(33)with the sets \(S_3\) and \(S_4\) as defined therein. Since \(S_3 \not \subseteq {\underline{Z1}}\), we get
$$\begin{aligned} {\underline{Z2}}= & {} {\underline{Z1}} - S_4 \\= & {} \{(x, y, 1, 2) | (x, y, 1, 2) \in Z\} - \\&(\{(j, u,1,2) \ | \ u \ne i, u \ne j\} \ \cup \ \{(u, j, 1, 2) \ | \ u \ne i, u \ne j\}) \end{aligned}$$This clearly means that, if j is one of the two top priority players, the other one must be i. This is the second implication given in the statement of this Lemma.
-
2.
\({\underline{Z1}} = \{(x, y, 1, 1) | (x, y, 1, 1) \in Z\}\): If the outcome of T2(i, j) is \(v(\pi ^1) \le v(\pi ^2)\) then, as per Theorem 9, we have the following.
$$\begin{aligned} {\underline{Z2}}= & {} {\overline{Z2}} - (S_1 \cup S_2) \nonumber \\= & {} {\underline{Z1}} - (S_1 \cup S_2) \end{aligned}$$(34)with the sets \(S_1\) and \(S_2\) as defined therein. Since \(S_1 \not \subseteq {\underline{Z1}}\), we get
$$\begin{aligned} {\underline{Z2}}= & {} {\underline{Z1}} - S_2 \\= & {} \{(x, y, 1, 1) | (x, y, 1, 1) \in Z\} - \\&(\{(j, u,1,1) \ | \ u \ne i, u \ne j\} \ \cup \ \{(u, j, 1, 1) \ | \ u \ne i, u \ne j\}) \end{aligned}$$This clearly means that, if j is one of the two top priority players, the other one must be i. This is the second implication given in the statement of this Lemma.
On the other hand, if the outcome of T2(i, j) is \(v(\pi ^1) \ge v(\pi ^2)\) then, as per Theorem 9, we have the following.
$$\begin{aligned} {\underline{Z2}}= & {} {\overline{Z2}} - (S_3 \cup S_4) \nonumber \\= & {} {\underline{Z1}} - (S_3 \cup S_4) \end{aligned}$$(35)with the sets \(S_3\) and \(S_4\) as defined therein. Since \(S_4 \not \subseteq {\underline{Z1}}\), we get
$$\begin{aligned} {\underline{Z2}}= & {} {\underline{Z1}} - S_3\\= & {} \{(x, y, 1, 1) | (x, y, 1, 1) \in Z\} - \\&(\{(i, u,1,1) \ | \ u \ne i, u \ne j\} \ \cup \ \{(u, i, 1, 1) \ | \ u \ne i, u \ne j\}) \end{aligned}$$This clearly means that, if i is one of the two top priority players, the other one must be j. This is the first implication given in the statement of this Lemma.
\(\square \)
As per Lemma 13, T2 is useful for doing eliminations as long as the set of possibilities contains at least two partner pairs. Thus, by repeating T2(i, j) with suitably varying i and j, all those players who are guaranteed to be neither \(P_1\) nor \(P_2\) can be eliminated from consideration. The way to set i and j for doing T2(i, j) is in the proof of Lemma 13. The condition for termination is in Lemma 14: stop doing T2 when the set of possibilities contains only one partner pair.

Observe that prior to doing T1, the set of all possibilities, Z, contains \(2 \times n \times (n-1)\) elements. After T1, the set of possibilities is reduced to \(n \times (n-1)\). When the termination condition (viz., fewer than two remaining partner pairs) for T2 is satisfied, the number of possibilities is reduced to two. Further, these two remaining possibilities form a partner pair. This is the end of Step 1 of our method for computing \(\pi ^{OPT}\). At this stage, we know exactly the two players who comprise the set \(P_1 \cup P_2\) although we do not know which one of these two players is \(P_1\) and which one is \(P_2\). However, knowledge about the identities of \(P_1\) and \(P_2\) is unnecessary as long as we know the precise two element set comprised of \(P_1\) and \(P_2\). The entire process for Step 1 is given in Algorithm 4.
Analysing the time complexity of Algorithm 4, Lines 1 and 2 take \({\mathcal {O}}(n^2)\) time. Line 3 takes constant time. Lines 4 takes \({\mathcal {O}}(n^2)\) time. Lines 5 to 7 take constant time. Lines 10, 11, and 12 take \({\mathcal {O}}(n^2)\), \({\mathcal {O}}(1)\) and \({\mathcal {O}}(n^2)\) time respectively. Since \({\overline{Z2}}\) initially contains \(n \times (n-1)\) elements, the while loop of Line 9 will take \({\mathcal {O}}(n^4)\) time. Given this, the if statement of Line 8 will take \({\mathcal {O}}(n^4)\) time. Similarly, the if statement of Line 20 will take \({\mathcal {O}}(n^4)\) time. The running time of Algorithm 4 will therefore be \({\mathcal {O}}(n^4)\).
Next, we will show how to determine the identities of the players \(P_3, \ldots , P_n\) and their respective optimal coalitions. This is Step 2 of our method. At the end of this step, \(\pi ^{OPT}\) will have been computed.
In more detail, the identities of \(P_3, \ldots , P_n\) will be found one by one, starting with \(P_3\). In general, \(P_i\) will be determined on the basis of the identities of \(P_1, \ldots , P_{i-1}\) and their respective optimal coalitions.
Let S denote the set of top i priority players \(P_1, \ldots , P_i\) whose identities are known. Suppose that each one of these i players belongs to one of the coalitions \(C^{OPT}_1, \ldots , C^{OPT}_A\), at least one of them belongs to \(C^{OPT}_A\), and none of them belongs to \(C^{OPT}_{A+1}\). Let \(R=N-S\) be the set of remaining players. Then, the player with priority \(P_{i+1}\) must be in R and must belong to one of the coalitions \(C^{OPT}_1, \ldots , C^{OPT}_{A+1}\) in \(\pi ^{OPT}\). There are \(|R|=n-i\) possibilities for the identity of \(P_{i+1}\) and \(A+1\) possibilities for its optimal coalition. Let V be a set containing all these possibilities:
The semantics of (x, y) is that x is a possible identity of the \(i+1\)th priority player and x belongs to \(C^{OPT}_y\) in \(\pi ^{OPT}\). Thus \(|V| = (n-i) \times (A+1)\).
Due to unique optimum, only one element of V will correspond to \(\pi ^{OPT}\) and the problem is find it. Suppose that this element is (a, b). Then, monotonicity induces the implication \(X_{a,b}\) given in Table 9. That is, any structure \(\pi ^1\) in which each player in S is in its optimal coalition (i.e., \(\beta ^{x \in S}_{\pi ^1}=\beta ^{x \in S}_{\pi ^{OPT}}\)), player a is in \(C^1_b\) (i.e., \(\beta ^a_{\pi ^1}=b\)) must have a higher value than any any structure \(\pi ^2\) in which each player in S is in its optimal coalition (i.e., \(\beta ^{x \in S}_{\pi ^2}=\beta ^{x \in S}_{\pi ^{OPT}}\)) and player a is not in in \(C^2_b\) (i.e., \(\beta ^a_{\pi ^2}\ne b\)). Given this implication, we will use the test T3 (see Table 10) to determine the identity of \(P_{i+1}\) and its optimal coalition, by eliminating those elements from V that do not correspond to \(\pi ^{OPT}\).
The test T3 takes four parameters a, b, c, and d such that (a, b) and (c, d) are two distinct elements in V, and compares the values of two structures \(\pi ^1\) and \(\pi ^2\) defined as follows. \(\pi ^1\) is any structure in which each player in S is in its respective optimal coalition (i.e., \(\beta ^{x \in S}_{\pi ^1}=\beta ^{x \in S}_{\pi ^{OPT}}\)), player a is in \(C^1_b\) (i.e., \(\beta ^a_{\pi ^1}=b\)), and player c is in any coalition except \(C^1_d\) (i.e., \(\beta ^c_{\pi ^1}\ne d\)). \(\pi ^2\) is any structure in which each player in S is in its respective optimal coalition (i.e., \(\beta ^{x \in S}_{\pi ^2}=\beta ^{x \in S}_{\pi ^{OPT}}\)), player c is in \(C^2_d\) (i.e., \(\beta ^c_{\pi ^2}=d\)), and player a is in any coalition except \(C^2_b\) (i.e., \(\beta ^a_{\pi ^2}\ne b\)). Theorem 10 is a formalization of the eliminations that result from the outcome of T3(a, b, c, d). As before, E will denote the set of eliminations.
Theorem 10
Suppose (a, b) and (c, d) are any two distinct elements of V. Depending on the result of T3(a, b, c, d), where T3 is as defined in Table 10, one or both of these elements will be eliminated from V.
Proof
The outcome of T3(a, b, c, d) must be one of the three possibilities: \(v(\pi ^1) < v(\pi ^2)\), \(v(\pi ^1) = v(\pi ^2)\), or \(v(\pi ^1) > v(\pi ^2)\). If \(v(\pi ^1) \le v(\pi ^2)\), then (a, b) must be eliminated from V. This is because the antecedant of the implication \(\overset{R}{\Rightarrow }\) of \(X_{a, b}\) in Table 9 is true but its consequent is false. This means that the consequent of the implication \(\overset{L}{\Rightarrow }\) is false, so by contrapositive, its antecedant must be false.

Analogously, if the result of T3(a, b, c, d) yields \(v(\pi ^1) \ge v(\pi ^2)\), then (c, d) must be eliminated. \(\square \)
Lemma 17
If \(|V| \ge 2\), T3 can be guaranteed to result in one or more eliminations.
Proof
As per Theorem 10, for any two distinct elements (a, b) and (c, d) of V, the test T3(a, b, c, d) will result in at least one elimination. \(\square \)
Lemma 18
If the eliminations from T3 result in an empty V, monotonicity is violated.
Proof
The basis of eliminations from T3 is the monotonicity induced implication of Table 9. Thus, if any elimination results in an empty V, monotonicity was violated. \(\square \)
By appropriately varying the parameters ab, c, and d, the test T3(a, b, c, d) can be used to determine the identity of \(P_{i+1}\) and its optimal coalition. Lemma 19 is a constructive proof of how this can be done.
Lemma 19
Suppose the identities and optimal coalitions for the i (\(i \ge 2\)) top priority players \(P_1, \ldots , P_i\) are known. To determine the identity of \(P_{i+1}\) and its optimal coalition, the test T3 must be performed at most \((n-i) \times (A+1) - 1\) times with appropriate parameters.
Proof
As per Theorem 10, for any two distinct elements (a, b) and (c, d) of V, the test T3(a, b, c, d) will result in at least one elimination. Since \(|V| = (n-i) \times (A+1)\), T3 must be performed at most \((n-i) \times (A+1) - 1\) times. \(\square \)
Based on Theorem 10 and Lemmas 17 to 19, \(P_{i+1}\) and its optimal coalition can be determined as follows.
-
Step 1
Choose any two elements from V, say \((a, b) \in V\) and \((c, d) \in V\).
-
Step 2
Perform the test T3(a, b, c, d).
-
Step 3
As per Theorem 10, any one or both of the following possibilities will be eliminated. Let E be the set of eliminations.
-
Step 4
Update V to \(V-E\).
-
Step 5
Repeat Steps 1 to 4 until V has more than one element.
After these steps, the only element left in V will be the pair whose first element is the identity of \(P_{i+1}\) and whose second element is its optimal coalition. By varying \(i+1\) between 3 and \(n-1\), \(P_3, \ldots , P_{n-1}\) and their respective optimal coalitions are found. Then the lowest priority player \(P_n\) will be the only remaining player, i.e., \(P_n = a\) where \(a \in N\) and \(a \notin \{P_1, \ldots , P_{n-1}\}\) and its optimal coalition will be \(C^{OPT}_b\) where
The structure \(\pi ^t\) for \(1 \le t \le A+1\) is defined as follows: for each \(x \in \{P_1, \ldots , P_{n-1}\}\), \(\beta ^x_{\pi ^i} = \beta ^x_{\pi ^{OPT}}\) and \(\beta ^a_{\pi ^i} = t\).

The above greedy method is formulated in Algorithm 5. Analysing its time complexity, Line 2 takes O(n) time while Line 3 \(O(n^2)\) time. Lines 5 and 6 take constant time. Since \(|V| \le (n-i)\times (A+1)\), the while loop of Line 4 will take \(O(n^2)\) time. The Lines 9 to 13 take constant time. The for loop of Line 1 therefore will take \(O(n^3)\) time. The Lines 15 to 17 take O(n) time. The time to run Algorithm 5 will be \(O(n^3)\).
The total time taken to compute the optimal structure \(\pi ^{OPT}\) will therefore be \(O(n^4)\) which is the sum of the times taken by Algorithms 4 and 5.
Section 7.2 is an illustration of this method for three player games.
7.2 An illustration for three-player games
Step 1 is to determine the two top priority players and their optimal coalitions. Figure 4 is a decision tree for Step 1. The non-leaf nodes of the tree are the tests. For each test, the resulting eliminations are shown in the grey boxes. Each leaf node is shown as a green box containing the two remaining possibilities. Initially, Z contains all twelve possibilities:
The first test, T1, shown in the root node compares the values of the structure containing the grand coalition and the one comprised of all singletons. If \(v(\pi ^G) < v(\pi ^S)\), then as per Theorem 9, the resulting eliminations will be
This is shown along the left branch of the root node in Fig. 4. On the other hand, if \(v(\pi ^G) > v(\pi ^S)\), then the resulting eliminations will be
This is shown along the right branch of the root node in Fig. 4. Along the middle branch, \(v(\pi ^G) = v(\pi ^S)\) and this is a violation of monotonicity.
At level 1 of the tree along the left branch, is the test T2(3, 2) which compares the values \(v((\{1,2\}\{3\}))\) and \(v((\{1,3\}\{2\}))\). The eliminations that result from the three different outcomes of this test are shown in the grey boxes. For \(v((\{1,2\}\{3\})) < v((\{1,3\}\{2\}))\), four possibilities remain after this elimination: (1, 2, 1, 2), (2, 1, 1, 2), (3, 2, 1, 2), and (2, 3, 1, 2). These four elements are of the form (i, x, 1, 2), (x, i, 1, 2), (j, x, 1, 2), and (x, j, 1, 2) where \(x=2\), \(i=1\), and \(j=3\). Thus, as per the proof of Lemma 13, the next test will be T2(1, 3) which compares the values \(v((\{1\}\{2,3\}))\) and \(v((\{1,2\}\{3\}))\). This is shown along the leftmost branch of the tree. For the case \(v((\{1\}\{2,3\})) < v((\{1,2\}\{3\}))\), the two top priority players are known to be the players 2 and 3 and they are known to belong to different coalitions in \(\pi ^{OPT}\). The remainder of the tree is constructed similarly. This is Step 1.
Step 2 is to determine the optimal coalition for the player with priority \(P_3\). Since it is a three player game, the identity of \(P_3\) will become known at the end of Step 1. Suppose that, at the end of Step 1, \(Z = \{(1,2,1,2), (2,1,1,2)\}\). Then there are three possibilities for \(P_3\)’s optimal coalition: \(C^{OPT}_1\), \(C^{OPT}_2\), and \(C^{OPT}_3\). Define the structures \(\pi ^1\), \(\pi ^2\), \(\pi ^3\) as follows: \(\pi ^1 = (\{1,3\},\{2\})\), \(\pi ^2 = (\{1\},\{2,3\})\) and \(\pi ^3 = (\{1\},\{2\},\{3\})\). Player 3 must belong to \(C^{OPT}_1\) if \(max(v(\pi ^1), v(\pi ^2), v(\pi ^3))\) = \(v(\pi ^1)\), to \(C^{OPT}_2\) if \(max(v(\pi ^1), v(\pi ^2), v(\pi ^3))\) = \(v(\pi ^2)\), and to to \(C^{OPT}_3\) if \(max(v(\pi ^1), v(\pi ^2), v(\pi ^3))\) = \(v(\pi ^3)\).
8 Applications
Many applications of cooperative games arise in combinatorial optimization problems [5, 9, 14]. As demonstrated in Tables 3 and 4, the metric introduced in Sect. 2 is useful for defining monotonicity for a wide variety of cooperative games. CFGs and PFGs provide a general prototype for modelling a number of combinatorial optimization problems. Our work preserves this generality by introducing the abstract notions of distance and monotonicity to capture application specific details. Likewise, \(q_{min}\) is also an abstract entity and its precise definition is application dependent. The remainder of this section gives a detailed account of the relevance of the monotonicity requirement and the meaning of \(q_{min}\) for three potential applications: machine-scheduling games, supply-chain games, and combinatorial auctions. The proposed methods are useful for such applications if an ordering over the players is known to exist but the ordering itself is unknown.
-
Machine-scheduling games:
In a typical job shop scheduling problem [6, 25], there is a set of non-identical jobs and a set of different machines. Each job must be allocated to a single machine but a machine may be allocated several jobs. There are temporal constraints on jobs, in that some jobs must be completed before certain other jobs can be started. The machines run in parallel but the jobs on a machine a run sequentially. The completion time of a job depends on the job and the machine it is run on. The objective is to assign jobs to machines such that the time to complete the jobs is minimised. Such a scheduling problem is analogous to a PFG because a job can be viewed as a player and a machine as a coalition of its assigned jobs. There must be cooperation and coordination within coalitions in that the jobs assigned to a machine must be ordered to optimise completion times taking into consideration the set up times needed to switch from one job to another. Externalities arise because the completion times of the jobs on a machine affect the start times of jobs on other machines. The objective function of a scheduling problem is analogous to the value function in a coalition game. Although such scheduling problems are generally computationally hard, they are easy under the monontonicity assumption. Suppose we know that any delay in the completion of certain jobs will cause delays in other jobs. More precisely, for any i (where \(1 \le i < n\)) any delay in the completion job i will have knock on effects that cause delays in the subsequent jobs \(i+1, \ldots , n\), such that the value of any structure in which players 1 to i agree with the optimum has a higher value than any coalition structure in which only the players 1 to \(i-1\) agree with the optimum. In other words, there is a known ordering on all the n jobs. The monotonicity condition applies to such a scenario. However, suppose that such an ordering is known only for the first few jobs \(1, \ldots , q_{min}\) of the sequence but not for the remaining jobs \(q_{min}+1, \ldots , n\). This is precisely the quasi-monotonicity condition. Finally, for those situations where the ordering of players is unknown, the method proposed in Sect. 7 is useful.
-
Supply-chain games:
Business applications of multiagent systems frequently require automated formation of supply chains [12, 24]. In many such settings, externalities play a significant role [15]. For example, AerogisticsFootnote 7 provided a platform for small and medium-size manufacturers of aircraft components to form on-line supply-chain coalitions so that they were able to bid for manufacturing projects that were too large for them individually. The externalities in this setting arose from the fact that all aircraft components had to ultimately conform to the same standards. Consequently, the cost of standardization procedures incurred by any coalition depended on the number and structure of other winning coalitions. Given these externalities, the aim is to form a supply-chain to minimize the cumulative cost of the projects. In such a scenario, some components are more crucial to the effective operation of an aircraft than others. For example, an aircraft engine matters more than any other component such as aircraft seats. Thus an engine manufacturer must be given the highest priority in the sense of being in the right coalition. Monotonicity is satisfied when all players (i.e., manufacturers) can be prioritized from high to low; the value of a coalition structure is then decreasing in its distance from the optimum. Quasi-monotonicity arises when only the players \(1, \ldots , q_{min}\) can be prioritized. Further, for those situations where the priorities are unknown, the method proposed in Sect. 7 is useful.
-
Combinatorial auctions:
In distributed problem solving, a manager auctioning out tasks to bidders aims to optimise some performance measure such as the total cost incurred or the task completion times [38]. A task is allocated to a single bidder but a bidder may be allocated several tasks. Externalities arise due to temporal inter-dependence between tasks. Such a scenario is analogous to the machine-scheduling games described above with tasks being akin to jobs and bidders to machines.
A number of further applications such as economic lot sizing, timetabling in sports and transportation, and workforce scheduling [25] fit the general framework of machine-scheduling games given above. For such applications, the proposed methods compute an optimal coalition structure on the basis of an ordering on the structures; their numeric values are not required.
8.1 Pros and cons of the distance metric
In the games described above, there is an ordering over the players and misplacing a high priority player is more detrimental than misplacing multiple lower priority players. The metric proposed in Sect. 3.1 is well suited to such games but not to those in which mis-placing a high priority player may have the same effect as mis-placing several lower priority players or even to those games in which there is no player ordering. When there is no player ordering, similarity between two structures could be given just in terms of the number of mis-placed players. One such measure is the minimum number of players that must be deleted from the structures to make them equal. This alternative measure function, call it \(d_{ALT}\), could be defined as follows in terms of the contraction of a coalition structure.
Definition 8
The contraction of a structure \(\pi = \{C_1, C_2, \ldots \}\) to a coalition \(S \subseteq N\) is defined as
The distance between any two structures is then
Theorem 11 is proof that \(d_{ALT}\) is a mteric.
Theorem 11
The distance function \(d_{ALT}\) satisfies all metric axioms.
Proof
Non-negativity is satisfied because \(d_{ALT}(\pi ^1, \pi ^2) \in \{0, \ldots , n-1\}\). Further, for any two structures, \(\pi ^1\) and \(\pi ^2\), \(d(\pi ^1, \pi ^2) = 0\) implies that \(\pi ^1=\pi ^2\) and \(\pi ^1=\pi ^2\) implies \(d(\pi ^1, \pi ^2) = 0\). Symmetry is trivially satisfied. To prove triangle inequality, consider three distinct arbitrary structures \(\pi ^1\), \(\pi ^2\), and \(\pi ^3\) with distances as shown in Fig. 1. The triangle inequality axiom requires \(d_1 \le d_2 + d_3\). Let \(S_1\) be the smallest coalition to which \(\pi ^1\) and \(\pi ^2\) must be contracted to make them equal. Let \(S_2\) be the smallest coalition to which \(\pi ^2\) and \(\pi ^3\) must be contracted to make them equal. Let \(S_3\) be the smallest coalition to which \(\pi ^1\) and \(\pi ^3\) must be contracted to make them equal. Then we have the following:
\(\square \)
Example 9 is an illustration of the measurement of distances using \(d_{ALT}\).
Example 9
Consider the following structures:
\(\pi ^1\) and \(\pi ^2\) can be made equal just by deleting player 3 from both structures. So, the distance between \(\pi ^1\) and \(\pi ^2\) will be \(d_{ALT}(\pi ^1, \pi ^2)=1\). In the same way, the distance between \(\pi ^1\) and \(\pi ^3\) will be \(d_{ALT}(\pi ^1, \pi ^3)=1\).
Consider the metric d of Sect. 3, in the context of Example 9. This metric gives \(d(\pi ^1, \pi ^2)=1/2\) while \(d(\pi ^1, \pi ^3)=1/6\). The structure \(\pi ^3\) is closer to \(\pi ^1\) than is \(\pi ^2\) because the mis-placed player 7 has a much lower priority than the mis-placed player 3. In contrast, as per \(d_{ALT}\), \(\pi ^1\) is equidistant from \(\pi ^2\) and \(\pi ^3\) because this metric considers only the number of mis-placed players but is insensitive to the priorities of the mis-placed players. In order to cater to games with unordered players, monotonicity would need to be defined in the context of \(d_{ALT}\) and corresponding methods devised for computing optimal structures. Note that \(d_{ALT}\) is not the only metric for sets, other metrics could be defined and that optimality is metric related and not absolute.
9 Related work
Although the complete set partitioning problem has been studied for over four decades [18,19,20], work on optimal partitioning in the context of PFGs has only just begun [44]. The following is a chronological summary of the progress made in the context of CFGs and PFGs.
Rothkopf et al. [32] studied the complete set partitioning problem in the context of combinatorial auctions. This work is similar to our research in that it focuses not on the entire search space but only on a restricted part of it in order to gain computational feasibility. However, there are a number of crucial differences. First, they considered only the complete set partitioning problem (i.e., CFGs) and for this particular problem, they devised computationally feasible solutions for a restricted part of the search space. In contrast, we consider not just the complete set partitioning problem but any kind of value function (i.e., non-separable, CFGs, and PFGs with positive only, negative only, and positive and negative externalities) that is quasi-monotonic. The second difference is in terms of the approaches: [32] restrict the size of search space by imposing constraints on the cardinality of coalitions and partitions to gain computational feasibility, while we allow all partitions but restrict to quasi-monotonic value functions.
In order to overcome the complexity of complete set partitioning, some methods for generating approximate solutions were developed. Shehory and Kraus [37] presented anytime greedy approximation method for the set partitioning and set covering problems in the context of task allocation in multiagent systems. Their approach to reduce computational complexity was to impose a restriction on the number of agents per coalition. The solution thus generated is guaranteed to be within a loose ratio bound from the optimum given the restriction on the number of agents. Later, Sandholm et al. [34] used a breadth first search (BFS) method for finding an approximate solution that guarantees that the solution is within a tight bound from optimum.
Sen and Dutta [35] employed genetic algorithms to approximately solve the complete set partitioning problem and empirically showed that their method outperforms a number of exact solution methods in many settings. This heuristic approach does not provide guarantees on the quality of the approximation.
In the context of winner determination in combinatorial auctions, Sandholm [33] presented an iterative deepening \(A^*\) (\(IDA^*\)) heuristic method with an admissible heuristic for solving the complete set partitioning problem in exponential time.
Rahwan and Jennings [26] proposed a faster and more memory efficient version of the dynamic programming method employed in [32] for the set partitioning problem. Again for CFGs, Rahwan et al. [29] used branch and bound and, through simulations, showed that pruning of the search space can be better accomplished by representing the search space in a certain way. Empirical evaluations showed that the solution can be generated faster than some of the other methods. Rahwan et al. [27, 28] also conducted one of the few studies of coalition structure generation for PFGs. However, they focused on PFGs with restricted externalities allowing positive only or negative only but not mixed externalities. This method has exponential time complexity.
Keinanen showed how simulated annealing can be used to generate an optimal coalition structure [17] for CFGs. They analyzed its performance in terms of various neighborhood operators. This being a heuristic approach, there is no guarantee on the quality of approximation.
For CFGs, Michalak et al. [23] showed how a branch and bound search can be improved by decentralising it whilst ensuring minimum inter-agent communication.
Ueda et al. [41] focused on CFGs and proposed an approximation method by assuming that the characteristic function is given as the optimal solution of a distributed constraint optimization problem. The approximate solution was shown to be within a constant factor of the optimal solution.
Di Mauro et al. [21] presented a greedy heuristic method for coalition structure generation for CFGs without giving any guarantee on the quality of approximation.
Banerjee and Kraemer [3] dealt with coalition structure generation for PFGs by defining agent types and assuming that externalities occur on the basis of types. Using a branch and bound method they empirically investigated the number of pruned partitions.
In a spirit similar to ours, but focusing only on CFGs, Bachrach et al. [2] proved polynomial time solvability by restricting the search space in a graph representation with bounded tree width. Aziz and de Keijzer [1] developed a polynomial time algorithm by imposing restrictions such as a fixed number on player types in CFGs and a fixed number of weights in weighted voting games. Ueda et al. [42] proposed a concise representation for characteristic functions in a similar vein to synergy coalition group representation [8] and MC-nets [16] but more compact than them.
Service and Adams [36] gave a constant factor approximation scheme for coalition structure generation for CFGs. Using dynamic programming they showed how their method could be used as an anytime algorithm.
Recently, Michalak et al. [22] conducted an extensive analysis of the search space for CFGs and showed that by combining dynamic programming with a tree search, it is possible to improve the search relative to methods using only dynamic programming or only tree search.
Table 11 provides a chronological summary of the developments that occurred over the last four decades. Compared to the methods listed above, the proposed approach is distinctive in that for the first time we show how a distance metric can be used for solving the optimal coalition structure determination problem. Another unique feature of the proposed methods is that they are suitable for any kind of monotonic value function, i.e., non-separable, CFGs, and PFGs with positive only, negative only, and mixed externalities. Existing literature has considered PFGs with positive only externalities, or else negative only externalities [28]. Mixed externalities were considered in [3] but only for one specific value function. Besides, our search methods require only an ordering on the values of partitions to be known but not their actual values. In contrast, the methods in the literature require the actual value of each coalition to be known, and assume that the value function is separable in that the value of each partition is simply the sum of the values of the coalitions in it. It remains unclear how to know these values, especially for large games.
10 Conclusions
This paper investigated the problem of computing an optimal coalition structure. For coalition games with an ordering over the players, a distance metric was introduced to measure the distance between any pair of coalition structures. For monotonic value functions and a known player ordering, a polynomial time greedy method was devised for searching for an optimal structure. It was shown how the method could be used for quasi-monotonic functions. Another polynomial time method was devised to compute the optimal coalition structure for a setting in which the value function is monotonic and an ordering over the players is known to exist but the ordering itself is unknown.
There are various avenues for further research. This paper focussed on coalition games with an ordering over the players. In many coalition games, players are unordered. How the proposed methods can be extended to such games remains to be investigated. With regard to the analysed setting for multiple optima, the optima themselves are close to each other. More general settings where the optima are far apart need further investigation. For such general settings, an optimum may not be computable in polynomial time and methods for computing approximately optimal structures would be needed.
Notes
Non-separable value functions are more general versions of the value functions employed in the literature on CFGs and PFGs. See Sect. 2 for details.
Recall that a coalition is a set of numbers. The smallest element of a coalition is then the smallest number in the set. For example, for the coalition \(C_1=\{2, 3, 4\}\), the smallest element is 2, i.e., \(min \ C_1 =2\).
An embedded coalition is a pair \((C, \pi )\) where \(C \in 2^N\) is a coalition in the sequence \(\pi \in \varPi _N\).
A partition \(\pi ^1\) is coarser than a partition \(\pi ^2\) if each coalition in \(\pi ^2\) is included in a coalition in \(\pi ^1\): if \(C_2 \in \pi ^2\), then \(C_2 \subseteq C_1\) for some \(C_1 \in \pi ^1\). Equivalently, \(\pi ^2\) is finer than \(\pi ^1\).
Observe that the setting in Sect. 3.1 corresponds to \(\varPi ^{\textsc {OPT}}\) containing an single element.
In Lemma 15, we prove that an empty Z marks a violation of monotonicity.
A British company located in Liverpool—see www.aerogistics.com for details.
References
Aziz, H., & de Keijzer, B. (2011). Complexity of coalition structure generation. In Proceedings of the 10th international joint conference on AAMAS (pp. 191–198).
Bachrach, Y., Meir, R., Jung, K., & Kohli, P. (2010). Coalitional structure generation in skill games. In Proceedings of AAAI (pp. 703–708).
Banerjee, B., & Kraemer, L. (2010). Coalition structure generation in multi-agent systems with mixed externalities. In Proceedings of AAMAS (pp. 175–182).
Bell, E. T. (1934). Exponential numbers. The American Mathematical Monthly, 41(7), 411–419.
Bitar, E., Baeyens, E., Khargonekar, P., Varaiya, P., & Poolla, K. (2012). Optimal sharing of quantity risk for a coalition of wind power producers facing nodal prices. In Proceedings of the 31st IEEE American control conference (pp. 4438–4445).
Brucker, P. (2007). Scheduling algorithms. Berlin: Springer.
Chalkiadakis, G., Elkind, E., & Wooldridge, M. (2011). Computational aspects of cooperative game theory. San Rafael: Morgan & Claypool.
Conitzer, V., & Sandholm, T. (2006). Complexity of constructing solutions in the core based on synergies among coalitions. AI Journal, 27, 381–417.
Curiel, I. (1997). Cooperative game theory and applications. Berlin: Springer.
de Bruijn, N. (1988). Asymptotic methods in analysis. Illinois: Dover.
De Clippel, G., & Serrano, R. (2008). Marginal contributions and externalities in the value. Econometrica, 76(6), 1413–1436.
Fink, A. (2006). Supply chain coordination by means of automated negotiations between autonomous agents. In B. Chaib-draa & J. Muller (Eds.), Multiagent based supply chain management (pp. 351–372). Berlin: Springer.
Garg, J., Mehta, R., & Vazirani, V. (2014). Dichotomies in equilibrium computation and complementary pivot algorithms for a new class of non-separable utility functions. In Proceedings of STOC.
Han, Z., & Poor, H. (2009). Coalition games with cooperative transmission: A cure for the curse of boundary nodes in selfish packet-forwarding wireless networks. IEEE Transactions on Communications, 57, 203–213.
Huq, G. (2010). Automated negotiation in multi-agent based electronic business: Negotiation in business-to-business transactions in supply chain management for multi-agent based electronic business. Muller: VDM Verlag Dr.
Ieong, S., & Shoham, Y. (2005). Marginal contribution nets: A compact representation scheme for coalitional games. In Proceedings of the ACM Conference on Electronic Commerce (pp. 193–202).
Keinanen, H. (2009). Simulated annealing for multi-agent coalition formation. In Proceedings of the Third KES international symposium on agent and multiagent systems: Technologies and applications KES-AMSTA (pp. 30–39).
Lin, C. (1975). Corporate tax structures and a special class of set partitioning problems. PhD thesis, Case Western Reserve University.
Lin, C., & Salkin, H. (1979). Aggregation of subsidiary firms for minimal unemployment compensation payments via integer programming. Management Science, 25(4), 405–408.
Lin, C., & Salkin, H. (1983). An efficient algorithm for the complete set partitioning problem. Discrete Applied Mathematics, 6, 149–156.
Di Mauro, N., Basile, T., Ferilli, S., & Esposito, F. (2010). Coalition structure generation with grasp. In Proceedings of the fourteenth international conference on AI: Methodology, systems and applications (pp. 111—120).
Michalak, T., Rahwan, T., Elkind, E., & Wooldridge, M. (2016). A hybrid exact algorithm for complete set partitioning. AI Journal, 230, 139–174.
Michalak, T., Sroka, J., Rahwan, T., Wooldridge, M., McBurney, P., & Jennings, N. (2010). A distributed algorithm for anytime coalition structure generation. In Proceedings of AAMAS (pp. 17–114).
Moyaux, T., Chaib-draa, B., & D’Amours, S. (2006). Supply chain management and multiagent systems: An overview. In B. Chaib-draa & J. Muller (Eds.), Multiagent based supply chain management (pp. 1–27). Berlin: Springer.
Pinedo, M. (2008). Scheduling: Theory, algorithms and systems. Berlin: Springer.
Rahwan, T., & Jennings, N. R. (2008). An improved dynamic programming algorithm for coalition structure generation. In In Proceedings of the seventh international joint conference on autonomous agents and multiagent systems (pp. 1417–1420).
Rahwan, T., Michalak, T., Jennings, N.R., Wooldridge, M., & McBurney, P. (2009). Coalition structure generation in multi-agent systems with positive and negative externalities. In In Proceedings of the 21st international joint conference on AI.
Rahwan, T., Michalak, T., Wooldridge, M., & Jennings, N. (2012). Anytime coalition structure generation in multi-agent systems with positive or negative externalities. AI Journal, 186, 95–122.
Rahwan, T., Ramchurn, S., Jennings, N., & Giovanucci, A. (2009). An anytime algorithm for optimal coalition structure generation. Journal of AI Research, 34, 521–567.
Ray, D. (2007). A game-theoretic perspective on coalition formation. Oxford: Oxford University Press.
Rota, G. (1964). The number of partitions of a set. American Mathematical Monthly, 71(5), 498–504.
Rothkopf, M., Pekec, A., & Harstad, R. (1998). Computationally manageable combinatorial auctions. Management Science, 44(8), 1131–1147.
Sandholm, T. (2002). Algorithm for optimal winner determination in combinatorial auctions. AI Journal, 135, 1–54.
Sandholm, T., Larson, K., Anderson, A., Shehory, O., & Tohme, F. (1999). Coalition structure generation with worst case guarantees. AI Journal, 111, 209–238.
Sen, S., & Dutta, P. (2000). Searching for optimal coalition structures. In Proceedings of ICMAS (pp. 286–292).
T. Service and J. Adams. (2011). Constant factor approximation algorithms for coalition structure generation. Journal of Autonomous Agents and MultiAgent Systems, 23, 1–17.
Shehory, O., & Kraus, S. (1998). Methods for task allocation via agent coalition formation. Artificial Intelligence Journal, 101(1–2), 165–200.
Smith, R. (1980). The contract net protocol: High level communication and control in a distributed problem solver. IEEE Transactions on Computers, C–29(12), 1104–1113.
Sutherland, W. (2009). Introduction to metric and topological spaces. Oxford: Oxford University Press.
Thrall, R., & Lucas, W. (1963). \(n\)-Person games in partition function form. Naval Research Logistics Quarerly, 10, 281–298.
Ueda, S., Iwasaki, A., & Yokoo, M. (2010). Coalition structure generation based on distributed constraint optimization. In Proceedings of AAAI (pp. 155–168).
Ueda, S., Iwasaki, A., & Yokoo, M. (2011). Concise characteristic function representations in coalitional games based on agent types. In Proceedings of IJCAI (pp. 393–399).
Yeh, D. (1986). A dynamic programming approach to the complete set partitioning problem. BIT Numerical Mathematics, 26(4), 467–474.
Yi, S. (2003). Endogenous formation of economic coalitions: A survey on the partition function approach. In C. Carraro (Ed.), The endogenous formation of economic coalitions (pp. 80–127). London: Edward Elgar.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fatima, S., Wooldridge, M. Computing optimal coalition structures in polynomial time. Auton Agent Multi-Agent Syst 33, 35–83 (2019). https://doi.org/10.1007/s10458-018-9398-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10458-018-9398-8








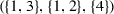 —because player 1 is a member of more than one coalition;
—because player 1 is a member of more than one coalition;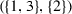 —because player 4 does not appear in any coalition;
—because player 4 does not appear in any coalition; —because
—because 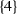 appears before
appears before 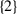 ;
;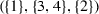 —because
—because 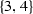 appears before
appears before  .
.


 if
if  if
if 