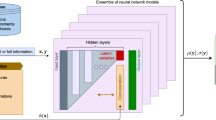
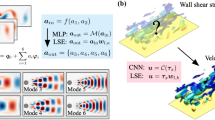
Abstract
In this work, we explore the advantages of end-to-end learning of multilayer maps offered by feedforward neural networks (FFNNs) for learning and predicting dynamics from transient flow data. While data-driven learning (and machine learning) in general depends on data quality and quantity relative to the underlying dynamics of the system, it is important for a given data-driven learning architecture to make the most of this available information. To this end, we focus on data-driven problems where there is a need to predict over reasonable time into the future with limited data availability. Such function time series prediction of full and reduced states is different from many applications of machine learning such as pattern recognition and parameter estimation that leverage large datasets. In this study, we interpret the suite of recently popular data-driven learning approaches that approximate the dynamics as Markov linear model in higher dimensional feature space as a multilayer architecture similar to neural networks. However, there exist a couple of key differences: (i) Markov linear models employ layer-wise learning in the sense of linear regression whereas neural networks represent end-to-end learning in the sense of nonlinear regression. We show through examples of data-driven modeling of canonical fluid flows that FFNN-like methods owe their success to leveraging the extended learning parameter space available in end-to-end learning without overfitting to the data. In this sense, the Markov linear models behave as shallow neural networks. (ii) The second major difference is that while the FFNN is by design a forward architecture, the class of Markov linear methods that approximate the Koopman operator is bi-directional, i.e., they incorporate both forward and backward maps in order to learn a linear map that can provide insight into spectral characteristics. In this study, we assess both reconstruction and predictive performance of temporally evolving dynamic using limited data for canonical nonlinear fluid flows including transient cylinder wake flow and the instability-driven dynamics of buoyant Boussinesq flow.
Similar content being viewed by others
References
Deem, E.A., Cattafesta, L.N., Yao, H., Hemati, M., Zhang, H., Rowley, C.W.: Experimental implementation of modal approaches for autonomous reattachment of separated flows. In: 2018 AIAA Aerospace Sciences Meeting, p 1052 (2018)
Edstrand, A.M., Schmid, P.J., Taira, K., Cattafesta, L.N.: A parallel stability analysis of a trailing vortex wake. J. Fluid Mech. 837, 858–895 (2018)
Wu, X., Moin, P., Wallace, J.M., Skarda, J., Lozano-Durán, A., Hickey, J.-P.: Transitional–turbulent spots and turbulent–turbulent spots in boundary layers. In: Proceedings of the National Academy of Sciences, p. 201704671 (2017)
Kim, J., Bewley, T.R.: A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417 (2007)
Brunton, S.L., Noack, B.R.: Closed-loop turbulence control: progress and challenges. Appl. Mech. Rev. 67(5), 050801 (2015)
Cao, Y., Zhu, J., Navon, I.M., Luo, Z.: A reduced-order approach to four-dimensional variational data assimilation using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 53(10), 1571–1583 (2007)
Fang, F., Pain, C., Navon, I., Gorman, G., Piggott, M., Allison, P., Farrell, P., Goddard, A.: A pod reduced order unstructured mesh ocean modelling method for moderate Reynolds number flows. Ocean Modell. 28(1–3), 127–136 (2009)
Benner, P., Gugercin, S., Willcox, K.: A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 57(4), 483–531 (2015)
Schmid, P.J.: Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28 (2010)
Rowley, C.W., Dawson, S.T.: Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417 (2017)
Rowley, C.W., Mezić, I., Bagheri, S., Schlatter, P., Henningson, D.S.: Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127 (2009)
Williams, M.O., Rowley, C.W., Kevrekidis, I.G.: A kernel-based approach to data-driven Koopman spectral analysis. ArXiv e-prints (2014)
Williams, M.O., Kevrekidis, I.G., Rowley, C.W.: A data–driven approximation of the koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 25(6), 1307–1346 (2015)
Jayaraman, B., Lu, C., Whitman, J., Chowdhary, G.: Sparse feature-mapped Markov models for nonlinear fluid flows. Computers and Fluids, https://doi.org/10.1016/j.compfluid.2019.104252 (2019)
Lu, C., Jayaraman, B.: Data-driven modeling for nonlinear fluid flows. In: 23rd AIAA Computational Fluid Dynamics Conference, vol. 3628, pp. 1–16 (2017)
Wu, H., Noé, F.: Variational approach for learning Markov processes from time series data, vol. 17. arXiv:https://arxiv.org/abs/1707.04659 (2017)
Xiao, D., Fang, F., Buchan, A., Pain, C., Navon, I., Muggeridge, A.: Non-intrusive reduced order modelling of the Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 293, 522–541 (2015)
Xiao, D., Fang, F., Pain, C., Hu, G.: Non-intrusive reduced-order modelling of the Navier-Stokes equations based on rbf interpolation. Int. J. Numer. Methods Fluids 79(11), 580–595 (2015)
Lusch, B., Kutz, J.N., Brunton, S.L.: Deep learning for universal linear embeddings of nonlinear dynamics, arXiv:https://arxiv.org/abs/1712.09707 (2017)
Pan, S., Duraisamy, K.: Long-time predictive modeling of nonlinear dynamical systems using neural networks, arXiv:https://arxiv.org/abs/1805.12547 (2018)
Otto, S.E., Rowley, C.W.: Linearly-recurrent autoencoder networks for learning dynamics, arXiv:https://arxiv.org/abs/1712.01378 (2017)
Wang, Q., Hesthaven, J.S., Ray, D.: Non-intrusive reduced order modeling of unsteady flows using artificial neural networks with application to a combustion problem. J. Comput. Phys. 384, 289–307 (2019)
Noack, B.R., Afanasiev, K., Morzyński, M., Tadmor, G., Thiele, F.: A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363 (2003)
Taira, K., Brunton, S.L., Dawson, S., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V., Ukeiley, L.S.: Modal analysis of fluid flows: an overview. AIAA 55(12), 4013–4041 (2017)
Bagheri, S.: Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623 (2013)
Berkooz, G., Holmes, P., Lumley, J.L.: The proper orthogonal decomposition in the analysis of turbulent flows. Ann. Rev. Fluid Mech. 25(1), 539–575 (1993)
Bishop, C., Bishop, C.M., et al.: Neural Networks for Pattern Recognition. Oxford University Press (1995)
Christopher, M.B.: Pattern Recognition and Machine Learning. Springer, New York (2016)
Mezić, I.: Spectral properties of dynamical systems, model reduction and decompositions. Nonlin. Dyn. 41(1), 309–325 (2005)
Koopman, B.O.: Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. 17(5), 315–318 (1931)
Allison, S., Bai, H., Jayaraman, B.: Wind estimation using quadcopter motion: A machine learning approach, arXiv:https://arxiv.org/abs/1907.05720 (2019)
Hopfield, J.J.: Neural networks and physical systems with emergent collective computational abilities. Proc. Nat. Acad. Sci. 79(8), 2554–2558 (1982)
Hochreiter, S., Schmidhuber, J.: Long short-term memory. Neur. Comput. 9(8), 1735–1780 (1997)
Soltani, R., Jiang, H.: Higher order recurrent neural networks, arXiv:https://arxiv.org/abs/1605.00064 (2016)
Yu, R., Zheng, S., Liu, Y.: Learning chaotic dynamics using tensor recurrent neural networks. In: Proceedings of the ICML 17 Workshop on Deep Structured Prediction, Sydney, Australia, PMLR 70 (2017)
Brunton, S.L., Brunton, B.W., Proctor, J.L., Kutz, J.N.: Koopman invariant subspaces and finite linear representations of nonlinear dynamical systems for control. PloS One 11(2), e0150171 (2016)
Bengio, Y., Simard, P., Frasconi, P.: Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 5(2), 157–166 (1994)
Bengio, Y., Goodfellow, I.J., Courville, A.: Deep learning. Nature 521 (7553), 436–444 (2015)
Brunton, S.L., Proctor, J.L., Kutz, J.N.: Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. 113(15), 3932–3937 (2016)
Rudy, S.H., Brunton, S.L., Proctor, J.L., Kutz, J.N.: Data-driven discovery of partial differential equations. Sci. Adv. 3(4), e1602614 (2017)
Schaeffer, H.: Learning partial differential equations via data discovery and sparse optimization. Pro. R. Soc. A Math. Phys. Eng. Sci. 473(2197), 20160446 (2017)
Long, Z., Lu, Y., Ma, X., Dong, B.: Pde-net: Learning pdes from data, arXiv:https://arxiv.org/abs/1710.09668 (2017)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics informed deep learning (part i): data-driven solutions of nonlinear partial differential equations, arXiv:https://arxiv.org/abs/1711.10561 (2017)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics informed deep learning (part ii): data-driven discovery of nonlinear partial differential equations, arXiv:https://arxiv.org/abs/1711.10566 (2017)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)
Reiss, J., Schulze, P., Sesterhenn, J., Mehrmann, V.: The shifted proper orthogonal decomposition: a mode decomposition for multiple transport phenomena. SIAM J. Sci. Comput. 40(3), A1322–A1344 (2018)
Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators. Neural Netw. 2(5), 359–366 (1989)
Puligilla, S.C., Jayaraman, B.: Deep multilayer convolution frameworks for data-driven learning of fluid flow dynamics. In: 24th AIAA Fluid Dynamics Conference, Aviation Forum, no. 3628, pp. 1–22 (2018)
Hinton, G.E., Salakhutdinov, R.R.: Reducing the dimensionality of data with neural networks. Science 313(5786), 504–507 (2006)
Bengio, Y.: On the challenge of learning complex functions. Prog. Brain Res. 165, 521–534 (2007)
Trefethen, L.N., Bau, IIID.: Numerical Linear Algebra, vol. 50. SIAM (1997)
Golub, G.H., Van Loan, C.F.: Matrix Computations, vol. 3. JHU Press (2012)
Roshko, A.: On the development of turbulent wakes from vortex streets NACA rep (1954)
Williamson, C.: Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627 (1989)
Cantwell, C.D., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., De Grazia, D., Yakovlev, S., Lombard, J. -E., Ekelschot, D., et al: Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219 (2015)
Weinan, E., Shu, C. -W.: Small-scale structures in boussinesq convection. Physics of Fluids (1998)
Liu, J.-G., Wang, C., Johnston, H.: A fourth order scheme for incompressible boussinesq equations. J. Sci. Comput. 18(2), 253–285 (2003)
Lele, S.K.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103(1), 16–42 (1992)
Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43(1), 89–112 (2001)
Acknowledgments
We acknowledge support from Oklahoma State University start-up grant and OSU HPCC for compute resources to generate the data used in this article. The authors thank Chen Lu, a former member of the Computational, Flow and Data Science research group at OSU, for providing the CFD data sets used in this article.
Author information
Authors and Affiliations
Contributions
BJ conceptualized the work with input from SCP. SCP developed the data-driven modeling codes used in this article with input from BJ. BJ and SCP analyzed the results. BJ developed the manuscript with contributions from SCP.
Corresponding author
Additional information
Communicated by: Anthony Patera
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Nomenclature and definitions
1.1 A.1 Nomenclature
F | = | nonlinear dynamical operator | λ | = | regularization parameter |
\(\mathcal {K}\) | = | Koopman operator | N | = | dimensions of state space |
\({\mathcal {K}_{a}}\) | = | approximate Koopman operator | M | = | dimensions of snapshots |
\(\mathcal {F}\) | = | functional space | K,R | = | dimension in features |
C | = | convolution operator | N f | = | neurons/feature growth |
factor | |||||
C m l | = | multilayer convolution operator | p i | = | i th-order polynomial |
g,h | = | observable functions | DMD | = | dynamic mode |
decomposition | |||||
x,y | = | state vectors | EDMD | = | extended dynamic mode |
(e.g., velocity field) | decomposition | ||||
X,Y | = | snapshot data pairs | POD | = | proper orthogonal |
decomposition | |||||
\(\bar X,\bar Y\) | = | POD weights data pairs | SVD | = | singular value |
decomposition | |||||
Θl | = | convolution operators or weights matrix | MSM | = | multilayer sequential map |
\(\mathcal {N}\) | = | nonlinear map | MEM | = | multilayer end-to-end map |
a | = | POD weights/coefficients | FFNN | = | feedforward neural networks |
\(\mathcal {J}\) | = | cost function | ()+ | = | pseudo-inverse |
\(\mathcal {LP}\) | = | learning parameter | \(\bar {()}\) | = | single convolution |
\(\bar {()}^{i}\) | = | multiple convolutions |
1.2 A.2 Definitions
\(\mathcal {LP} \) for MSMs | : | Number of elements in matrix (\(\mathcal {K}_{a}\)). |
: | For example, \(\mathcal {K}_{a}\) with size [9,9] has \(\mathcal {LP}\) = 81. | |
\(\mathcal {LP} \) for MEMs | : | Summation of all of elements in weight matrices |
(Θ’s). For example, a two hidden layer network | ||
: | with Nf = 3 has three weight matrices with | |
sizes Θ1 = [3, 9], Θ2 = [9, 9], Θ3 = [9, 3]. | ||
: | The \(\mathcal {LP} = 3\mathrm {x}9 + 9\mathrm {x}9 + 9\mathrm {x}3 = 135 \) | |
Feature growth factor (Nf) | : | Helps calculate the number hidden units or |
Neurons (Nh) in feedforward neural network | ||
: | based on the number of features(K) used | |
for the model. | ||
: | For example, with Nf = 3 and 3 features, the | |
number of neurons in each hidden layer | ||
would be 9 |
Polynomial feature growth pi | : | Order of polynomial used to grow the input |
features to learn MSM models. | ||
: | With 3 features and polynomial order of 2, | |
the feature growth would be 9. |
Appendix B: Learning parameter budget and POD space dimension
The number of learning parameters are dependent on the size of input POD space dimension and also the choice of model. For example, the MSM model with DMD architecture learns \(\mathcal {LP}\) parameters that has a quadratic dependence on the POD space dimension, K or \(\mathcal {LP} \propto O(K^{2})\). However, for the MSM/EDMD architecture, it turns out that \(\mathcal {LP}\) depends on the extended functional basis dimension which is usually Nf(K) ∗ K. Here, Nf(K) is a prefactor to K that also depends on K. Therefore, \(\mathcal {LP} \propto O((N_{f}(K)*K)^{2})\) to yield a super quadratic dependence on K. In fact, for P2, \(N_{f}(K)\sim K\) whereas for P7, \(N_{f}(K)\sim 40N\) when K = 3. For the MEM/FFNN methods, \(\mathcal {LP}\) depends on both N, the neuron growth factor, Nf, and number of layers , L, i.e., \(\mathcal {LP} \propto O((N_{f}*N)^{2}L)\). Typically, in our studies, Nf and L tend to be independent of N and therefore, \(\mathcal {LP}\) a shows quadratic dependence on the POD-space dimension.
Appendix C: Algorithm complexity
The cost of computing \(\mathcal {K}_{a}\) is directly related to number of input features, feature growth factor, and method used. In fact, this is not dissimilar to the parameter budgets discussed above. For the MSM method, where g,h are precomputed, we use Moore–Penrose inverse (pinv in MATLAB) for computing the transfer operator \(\mathcal {K}_{a}\) using least squares error minimization. Given K features and M snapshots, the cost of computing the pseudo-inverse is O(M xK2) and the estimation of the evolved state, YX+ requires order O(K xM2). Therefore, the total complexity is O(KM ∗ (M + K)). When K ≪ M, the complexity of the MSM model learning is O(KM2) and O(K2M) otherwise.
For the MSM method with EDMD-P2, i.e., using 2nd-order polynomial features, the feature dimension R grows as K + K(K + 1)/2. In this case, computational cost of estimating \(\mathcal {K}_{a}\) is of order O(M2xK2 + M xK4). When using higher order polynomial such as in EDMD-P7, computational cost is expected to depend on higher powers of K. Therefore, EDMD methods become expensive when using a higher dimensional POD space. For example, even a 2nd-order polynomial can become a limiting factor with large initial feature set, say, 50 POD modes and 400 snapshots, the resulting \(\mathcal {K}_{a}\) matrix would be of size [1325,1325] and the number of elements stored and computed is O(1, 755, 625), O(212 × 106) operations, respectively.
The computation cost of MEM (FFNN) method primarily depends on the number of hidden layers (L) and feature growth factor (Nf). The method consists a forward sweep of matrix multiplications, error/cost estimation, and backsweep of predominantly matrix multiplications for computing backpropagation. A single forward propagation operation consists of matrix multiplications based on the number of hidden layers (L) and number of elements in the hidden layers (NfxK). The computational cost associated with single forward propagation is of order O((L + 1)xNfxK xM). For Niter iterations, the order of computations would be O(Niterx(L + 1)xNfxK xM). Similarly, the cost of computation for backpropagation is also of the orderO(Niterx(L + 1)xNfxK xM). For example, given 50 POD modes and 400 snap shots, Nf = 3 with 2 hidden layers, the number of elements stored and computational cost are O(67500), O(Niterx1.8x106) operations, respectively.
Further, the cost of computing the POD basis is of order O(N xM2), where N is the dimension of full state vector. In the case of reconstruction, the computing cost is of the order O(N xK xM).
Appendix D: Effect of bias on predictions
The results presented in the main sections of this article for MEM architectures were based on FFNNs devoid of the bias term. It is well known from machine learning literature [47] that the presence of a bias term helps with function approximation provided sufficient \(\mathcal {LP}\)s are used to capture the dynamics. In our studies, the FFNN had difficulty predicting the shift mode for the transient cylinder wake dynamics (Section ??) whereas the modes with zero mean were predicted accurately. Since the bias term helps in quantitative translation (shift) of the learned dynamics into higher or lower values, we expect its inclusion to improve predictions. In Fig. 25, we show predictions of the features obtained from FFNNs with Nf = 1, 3, 9 for the TR-I regime for the cylinder flow with Re = 100. In Fig. 26, we include the predictions for the TR-II cylinder flow data. In both these cases, the shift mode (third POD feature) is accurately predicted with a bias term. Fig. 27 shows the corresponding predictions with bias term for the Boussinesq flow.
Rights and permissions
About this article
Cite this article
Puligilla, S.C., Jayaraman, B. Assessment of end-to-end and sequential data-driven learning for non-intrusive modeling of fluid flows. Adv Comput Math 46, 55 (2020). https://doi.org/10.1007/s10444-020-09753-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10444-020-09753-7