Abstract
Well-balanced schemes, nowadays mostly developed for both hyperbolic and kinetic equations, are extended in order to handle linear parabolic equations, too. By considering the variational solution of the resulting stationary boundary-value problem, a simple criterion of uniqueness is singled out: the \(C^{1}\) regularity at all knots of the computational grid. Being easy to convert into a finite-difference scheme, a well-balanced discretization is deduced by defining the discrete time-derivative as the defect of \(C^{1}\) regularity at each node. This meets with schemes formerly introduced in the literature relying on so-called ℒ-spline interpolation of discrete values. Various monotonicity, consistency and asymptotic-preserving properties are established, especially in the under-resolved vanishing viscosity limit. Practical experiments illustrate the outcome of such numerical methods.





Similar content being viewed by others
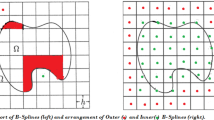
Notes
See (for instance) http://dlmf.nist.gov/12.2.
References
Adam, D., Felgenhauer, A., Roos, H.-G., Stynes, M.: A nonconforming finite element method for a singularly perturbed boundary value problem. Computing 54, 1–25 (1995)
Ahlberg, J.H., Nilson, E.N., Walsh, J.L.: Fundamental properties of generalized splines. Proc. Natl. Acad. Sci. USA 52(6), 1412–1419 (1964)
Ainsworth, M., Dorfler, W.: Fundamental systems of numerical schemes for linear convection-diffusion equations and their relationship to accuracy. Computing 66, 199–229 (2001)
De, D.N., Allen, G.: A suggested approach to finite difference representation of differential equations. Q. J. Mech. Appl. Math. 15, 11–33 (1962)
Amadori, D., Gosse, L.: Error estimates for well-balanced schemes on simple balance laws: one-dimensional position-dependent models. BCAM SpringerBriefs in Mathematics (2015)
Babuska, I., Osborn, J.E.: Generalized finite element methods: their performance and their relation to mixed methods. SIAM J. Numer. Anal. 20, 510–536 (1983)
Bao, W.Z., Jin, S.: The random projection method for stiff multi-species detonation capturing. J. Comput. Phys. 178, 37–57 (2002)
Berger, A.E., Solomon, J.M., Ciment, M.: An analysis of a uniformly accurate difference method for a singular perturbation problem. Math. Comput. 37, 79–94 (1981)
Berger, A.E., Han, H., Kellogg, R.B.: A priori estimates and analysis of a numerical method for a turning point problem. Math. Comput. 42, 465–492 (1984)
Buffa, A., Monk, P.: Error estimates for the ultra weak variational formulation of the Helmholtz equation. ESAIM: M2AN 42, 925–940 (2008)
Canosa, J., Gomes De Oliveira, R.: A new method for the solution of the Schrodinger equation. J. Comput. Phys. 5, 188–207 (1970)
McCartin, B.J.: Computation of exponential splines. SIAM J. Sci. Comput. 11, 242–262 (1990)
Cessenat, O., Despres, B.: Application of an ultra-weak variational formulation of elliptic PDE’s to the two-dimensional Helmholtz problem. SIAM J. Numer. Anal. 35, 255–299 (1998)
Champion, R., Lenard, C.T., Mills, T.M.: A variational approach to splines. ANZIAM J. 42, 119–135 (2000)
Cheung, Y.K., Jin, W.G., Zienkiewicz, O.C.: Direct solution procedure for solution of harmonic problems using complete, non-singular, Trefftz functions. Commun. Appl. Numer. Methods 5, 159–169 (1989)
Despres, B., Buet, Ch.: The structure of well-balanced schemes for Friedrichs systems with linear relaxation. Appl. Math. Comput. 272, 440–459 (2016)
Weinan, E.: Homogenization of scalar conservation laws with oscillatory forcing terms. SIAM J. Appl. Math. 52, 959–972 (1992)
Farrell, P.A., Gartland, E.C. Jr: A uniform convergence result for a turning point problem. In: BAIL V, Shanghai, 1988. Boole Press Conf. Ser., vol. 12, pp. 127–132 (1988)
Gartland, E.C. Jr.: Discrete weighted mean approximation of model convection-diffusion equation. SIAM J. Sci. Stat. Comput. 3, 460–472 (1982)
Gartland, E.C. Jr.: Strong stability of compact discrete boundary value problems via exact discretizations. SIAM J. Numer. Anal. 25, 111–123 (1988)
Gartland, E.C. Jr.: On the uniform convergence of the Scharfetter-Gummel discretization in one dimension. SIAM J. Numer. Anal. 30, 749–758 (1993)
Gil, A., Segura, J., Temme, N.: Computing the real parabolic cylinder functions \(U(a,x)\), \(V(a,x)\). ACM Trans. Math. Softw. 32, 70–101 (2006)
Glimm, J., Sharp, D.H.: An \(S\)-matrix theory for classical nonlinear physics. Found. Phys. 16, 125–141 (1986)
Gosse, L.: Computing Qualitatively Correct Approximations of Balance Laws. Exponential-Fit, Well-Balanced and Asymptotic-Preserving. SIMAI Springer Series (2013). ISBN 978-88-470-2891-3
Gosse, L.: Dirichlet-to-Neumann mappings and finite-differences for anisotropic diffusion. Comput. Fluids 156, 58–65 (2017). doi:10.1016/j.compfluid.2017.06.026
Gosse, L., LeRoux, A.Y.: Un schéma-équilibre adapté aux lois de conservation scalaires non-homogènes. C. R. Acad. Sci. Paris Sér. I 323, 543–546 (1996)
Greenberg, J., LeRoux, A.Y.: A well balanced scheme for the numerical processing of source terms in hyperbolic equations. SIAM J. Numer. Anal. 33, 1–16 (1996)
Han, H., Huang, Z., Kellogg, R.B.: A tailored finite point method for a singular perturbation problem on an unbounded domain. J. Sci. Comput. 36, 243–261 (2008)
Herrera, I.: The algebraic theory approach for ordinary differential equations: highly accurate finite differences. Numer. Methods Partial Differ. Equ. 3, 199–218 (1987)
Huang, L., Liu, T.P.: A conservative, piecewise-steady difference scheme for transonic nozzle flow. Comput. Math. Appl. 12A, 377–388 (1986)
Isaacson, E., Temple, B.: Convergence of the \(2 \times 2\) Godunov method for a general resonant nonlinear balance law. SIAM J. Appl. Math. 55, 625–640 (1995)
Kuo, C.C.J., Levy, B.: Mode-dependent finite-difference discretization of linear homogeneous differential equations. SIAM J. Sci. Comput. 9, 992–1015 (1988)
Jerome, J.W.: On uniform approximation by certain generalized spline functions. J. Approx. Theory 7, 143–154 (1973)
Jerome, J.W.: Analysis of Charge Transport: Mathematical Theory of Semiconductor Devices. Springer, Berlin (1996)
Kimmeldorf, G.S., Wahba, G.: The correspondence between Bayesian estimation on stochastic processes and smoothing by splines. Ann. Math. Stat. 41, 495–502 (1970)
Kita, E., Kamiya, N.: Trefftz method: an overview. Adv. Eng. Softw. 24, 3–12 (1995)
LeVeque, R.J., Yee, H.: A study of numerical methods for hyperbolic equations with stiff source terms. J. Comput. Phys. 86(1), 187–210 (1990)
Liu, T.P.: Quasilinear hyperbolic systems. Commun. Math. Phys. 68, 141–172 (1979)
Makarov, V.L., Samarskii, A.A.: Application of exact difference schemes to estimation of the convergence rate of the method of lines. Sem. Inst. Prikl. Mat. Dokl. 14, 18–23 (1980)
Niijima, K.: A uniformly convergent difference scheme for a semilinear singular perturbation problem. Numer. Math. 43, 175–198 (1984)
O’Malley, R.: On boundary value problems for a singularly perturbed differential equation with a turning point. SIAM J. Math. Anal. 1, 479–490 (1970)
O’Malley, R.: Singular Perturbation Methods for Ordinary Differential Equations. Springer, Berlin (1991)
Osher, S.: Nonlinear singular perturbation problems and one-sided difference schemes. SIAM J. Numer. Anal. 18, 129–144 (1981)
Pruess, S.: Estimating the eigenvalues of Sturm-Liouville problems by approximating the differential equation. SIAM J. Numer. Anal. 10, 55–68 (1973)
Roos, H.-G.: Global uniformly convergent schemes for a singularly perturbed boundary-value problem using patched base spline-functions. J. Comput. Appl. Math. 29, 69–77 (1990)
Roos, H.-G.: An analytically oriented discretization technique for boundary value problems. Abh. Math. Semin. Univ. Hamb. 61, 139–152 (1991)
Roos, H.-G., Stynes, M., Tobiska, L.: Robust Numerical Methods for Singularly Perturbed Differential Equations. Convection-Diffusion-Reaction and Flow Problems, 2nd edn. Springer Series in Computational Mathematics, vol. 24 (2008). ISBN 978-3-540-34466-7
Salama, A.A., Zidan, H.Z.: Fourth-order schemes of exponential type for singularly perturbed parabolic partial differential equations. Rocky Mt. J. Math. 36, 1049–1068 (2006)
Samarskii, A.A.: The Theory of Difference Schemes. Monographs and Textbooks in Pure and Applied Mathematics, vol. 240. Dekker, New York (2001). ISBN 0-8247-0468-1
Scharfetter, H.L., Gummel, H.K.: Large signal analysis of a silicon Read diode oscillator. IEEE Trans. Electron Devices 16, 64–77 (1969)
Schmidt, E., Lancaster, P., Watkins, D.: Bases of splines associated with constant coefficient differential operators. SIAM J. Numer. Anal. 12, 630–645 (1975)
Schultz, M.H., Varga, R.S.: \(L\)-splines. Numer. Math. 10, 345–369 (1967)
Schumaker, L.L.: Spline Functions: Basic Theory, 3rd edn. Cambridge University Press, Cambridge (2007). ISBN 978-0-521-70512-7
Shevaldin, V.-T.: Approximation by local \(L\)-splines corresponding to a linear differential operator of the second order. Proc. Steklov Inst. Math. 6, S178–S196 (2006)
Sod, G.A.: A random choice method with application to reaction-diffusion systems in combustion. Comput. Math. Appl. 11, 129–144 (1985)
Temme, N.: Numerical and asymptotic aspects of parabolic cylinder functions. J. Comput. Appl. Math. 121, 221–246 (2000)
Tikhonov, A.N., Samarskii, A.A.: Homogeneous difference schemes. USSR Comput. Math. Math. Phys. 1, 5–67 (1962)
Trefftz, E.: Ein gegenstuck zum Ritz’schen verfahren. In: Proc. 2nd Int. Congr. Appl. Mech., Zurich, pp. 131–137 (1926)
van Leer, B.: On the relation between the upwind-differencing schemes of Godunov, Engquist-Osher and Roe. SIAM J. Sci. Stat. Comput. 5, 1–20 (1984)
Wang, H.: Convergence of a numerical method for solving discontinuous Fokker–Planck equations. SIAM J. Numer. Anal. 45, 1425–1452 (2007)
Author information
Authors and Affiliations
Corresponding author
Appendix: An External Force \(f(x)\) in a Reaction-Diffusion Equation
Appendix: An External Force \(f(x)\) in a Reaction-Diffusion Equation
Hereafter, the aim is to solve the initial-boundary problem,
so that the resulting scheme recovers exactly the collection of points \(v(x_{j})\), for \(x_{j} \in \Delta \) the nodes of the grid. So, at each time-step \(t^{n}\), the “ℒ-spline” interpolation of the data \(u_{j}^{n}\) proceeds by solving the stationary equation between \(u_{j}^{n}\) and \(u_{j+1}^{n}\). Since, in \((x_{j},x_{j+1})\), both \(\bar{q}\) and \(\bar{f}\) are constant, each “local profile” is obtained by a standard “variation of constants” technique involving exponential functions:
-
let \(r_{j-\frac{1}{2}}=\sqrt{\bar{q}/\varepsilon }>0\) in \((x_{j-1},x _{j})\) and \(M_{j-\frac{1}{2}}\) be the matrix in,
$$ \left ( \textstyle\begin{array}{c} u_{j-1}^{n} - \frac{\bar{f}}{\bar{q}} \\ u_{j}^{n} - \frac{\bar{f}}{\bar{q}} \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c@{\quad}c} \exp (r_{j-\frac{1}{2}} x_{j-1}) & \exp (-r_{j-\frac{1}{2}} x_{j-1}) \\ \exp (r_{j-\frac{1}{2}} x_{j}) & \exp (-r_{j-\frac{1}{2}} x_{j}) \\ \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} A \\ B \end{array}\displaystyle \right ) . $$Yet the determinant \(|M_{j-\frac{1}{2}}|= -2\sinh (r_{j-\frac{1}{2}} \Delta x)\neq0\).
-
By mimicking Corollary 1, inside \((x_{j-1},x_{j})\),
$$ v'(x)=r_{j-\frac{1}{2}} \bigl(A \exp (r_{j-\frac{1}{2}} x) - B \exp (-r _{j-\frac{1}{2}} x) \bigr), $$and since \(M_{j\pm \frac{1}{2}}\) are invertible, \(C^{1}\) smoothness is just:
$$\begin{aligned} &r_{j-\frac{1}{2}}\Biggl\langle \left ( \textstyle\begin{array}{c} u_{j-1}^{n} - \frac{\bar{f}}{\bar{q}} \\ u_{j}^{n} - \frac{\bar{f}}{\bar{q}} \end{array}\displaystyle \right ) , M_{j- \frac{1}{2}}^{-T}\left ( \textstyle\begin{array}{c} \exp (r_{j-\frac{1}{2}} x_{j}) \\ -\exp (-r_{j-\frac{1}{2}} x_{j}) \end{array}\displaystyle \right ) \Biggr\rangle \\ &\quad =r_{j+\frac{1}{2}}\Biggl\langle \left ( \textstyle\begin{array}{c} u_{j}^{n} - \frac{\bar{f}}{\bar{q}} \\ u_{j+1}^{n} - \frac{\bar{f}}{\bar{q}} \end{array}\displaystyle \right ) , M_{j+ \frac{1}{2}}^{-T}\left ( \textstyle\begin{array}{c} \exp (r_{j+\frac{1}{2}} x_{j}) \\ -\exp (-r_{j+\frac{1}{2}} x_{j}) \end{array}\displaystyle \right ) \Biggr\rangle , \end{aligned}$$(A.2)where we have used the adjoint of the inverse matrices \(M_{j\pm \frac{1}{2}}^{-1}\) so that we don’t need the values of \(A,B\). Of course, the \(( \frac{\bar{f}}{\bar{q}} ) _{j \pm \frac{1}{2}}\) are different on both sides of the equality. By developing (A.2),
$$\begin{aligned} &\frac{u_{j}^{n+1}-u_{j}^{n}}{\Delta t}-\frac{\varepsilon }{\Delta x} \biggl[ \frac{r_{j+\frac{1}{2}}}{\sinh (r_{j+\frac{1}{2}}\Delta x)} \bigl( u_{j+1}^{n}-\cosh (r_{j+\frac{1}{2}}\Delta x)u_{j}^{n} \bigr) \\ &\quad {}-\frac{r_{j-\frac{1}{2}}}{\sinh (r_{j-\frac{1}{2}}\Delta x)} \bigl( \cosh (r _{j-\frac{1}{2}}\Delta x)u_{j}^{n}-u_{j-1}^{n} \bigr) \\ &\quad {}+r_{j+\frac{1}{2}}\frac{\cosh (r_{j+\frac{1}{2}}\Delta x)-1}{\sinh (r _{j+\frac{1}{2}}\Delta x)} \cdot \biggl( \frac{\bar{f}}{\bar{q}} \biggr) _{j + \frac{1}{2}} \\ &\quad {} +r_{j-\frac{1}{2}}\frac{\cosh (r_{j-\frac{1}{2}}\Delta x)-1}{ \sinh (r_{j-\frac{1}{2}}\Delta x)}\cdot \biggl( \frac{\bar{f}}{\bar{q}} \biggr) _{j - \frac{1}{2}} \biggr] =0. \end{aligned}$$Consistency can be established proceeding like in Proposition 2.
Rights and permissions
About this article
Cite this article
Gosse, L. ℒ-Splines and Viscosity Limits for Well-Balanced Schemes Acting on Linear Parabolic Equations. Acta Appl Math 153, 101–124 (2018). https://doi.org/10.1007/s10440-017-0122-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10440-017-0122-5
Keywords
- Constant/Line Perturbation method (C/L-PM)
- Fundamental system of solutions
- ℒ-spline
- Monotone well-balanced scheme
- Parabolic Cylinder functions (PCF)
- Vanishing viscosity



