Skip to main content
SpringerLink
Log in

Dispersive behavior of high frequency Rayleigh waves propagating on an elastic half space

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

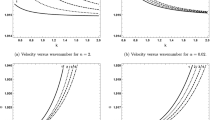
When the wavelength of Rayleigh wave is comparable with nanometers, Rayleigh wave will become dispersive. Such an interesting phenomenon cannot be predicted by the classical theory of elastodynamics. In order to reveal the internal mechanism and influencing factors of the dispersion, a model of Rayleigh wave propagating on an elastic half space is established and analyzed by a new theory of surface elastodynamics, in which the surface effect characterized by both the surface energy density and surface inertia is introduced. Two intrinsic nano-length scales, including the ratio of bulk surface energy density to bulk shear modulus and the ratio of surface mass density to bulk mass density, are achieved. It is found that when the wavelength of Rayleigh wave is comparable with the two intrinsic nano-lengths, the surface effect becomes significant. As a result, dispersion of Rayleigh wave happens and even two Rayleigh waves with different wave speeds may appear. Furthermore, it is found that the effect of surface energy density would enhance the wave speed, while that of surface inertia would reduce it. With the increase of wavelength, both effects gradually disappear and the Rayleigh wave speed degenerates to the classical one. The results of this paper are not only helpful to understand the dispersive mechanism of elastic waves, but also helpful for the fine design and measurement of nanowave devices.

Graphic abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Lange, K.: Bulk and surface acoustic wave sensor arrays for multi-analyte detection: a review. Sensors 19, 5382 (2019)

    Article  Google Scholar 

  2. Graff, K.F.: Wave Motion in Elastic Solids. Dover Publications, New York (2012)

    MATH  Google Scholar 

  3. Enzevaee, C., Shodja, H.M.: Crystallography and surface effects on the propagation of Love and Rayleigh surface waves in fcc semi-infinite solids. Int. J. Solids Struct. 138, 109–117 (2018)

    Article  Google Scholar 

  4. He, J., Zhao, J.: Finite element simulations of surface effect on Rayleigh waves. AIP Adv. 8, 035006 (2018)

    Article  Google Scholar 

  5. Shuttleworth, R.: The surface tension of solids. Proc. Phys. Soc. Lond. Sect. A 63, 444 (1950)

    Article  Google Scholar 

  6. Velasco, V.R., Garciamoliner, F.: Surface effects in elastic surface waves. Phys. Scr. 20, 111–120 (1979)

    Article  MathSciNet  Google Scholar 

  7. Gurtin, M.E., Murdoch, A.I.: A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 57, 291–323 (1975)

    Article  MathSciNet  Google Scholar 

  8. Timoshenko, S., Goodier, J.: Theory of Elasticity. McGraw Hill, New York (1951)

    MATH  Google Scholar 

  9. Li, M., Zhang, H.X., Zhao, Z.L., et al.: Surface effects on cylindrical indentation of a soft layer on a rigid substrate. Acta Mech. Sin. 36, 422–429 (2020)

    Article  MathSciNet  Google Scholar 

  10. Kired, M.R., Hachi, B.E., Hachi, D., et al.: Effects of nano-voids and nano-cracks on the elastic properties of a host medium: XFEM modeling with the level-set function and free surface energy. Acta Mech. Sin. 35, 799–811 (2019)

    Article  MathSciNet  Google Scholar 

  11. Gurtin, M.E., Murdoch, A.I.: Surface stress in solids. Int. J. Solids Struct. 14, 431–440 (1978)

    Article  Google Scholar 

  12. Murdoch, A.: The propagation of surface waves in bodies with material boundaries. J. Mech. Phys. Solids 24, 137–146 (1976)

    Article  Google Scholar 

  13. Qiang, F., Wei, P., Liu, X.: Propagation of elastic wave in nanoporous material with distributed cylindrical nanoholes. Sci. China Ser. G 56, 1542–1550 (2013)

    Article  Google Scholar 

  14. Peng, X.L., Huang, G.Y.: Elastic vibrations of a cylindrical nanotube with the effect of surface stress and surface inertia. Phys. E 54, 98–102 (2013)

    Article  Google Scholar 

  15. Cai, B., Wei, P.: Surface/interface effects on dispersion relations of 2D phononic crystals with parallel nanoholes or nanofibers. Acta Mech. 224, 2749–2758 (2013)

    Article  MathSciNet  Google Scholar 

  16. Qiang, F., Wei, P.: Effective dynamic properties of random nanoporous materials with consideration of surface effects. Acta Mech. 226, 1201–1212 (2015)

    Article  MathSciNet  Google Scholar 

  17. Kong, Z., Wei, P.J., Jiao, F.Y.: Surface/interface effects on the effective propagation constants of coherent waves in composites with random parallel nanofibers. J. Acoust. Soc. Am. 140, 486–497 (2016)

    Article  Google Scholar 

  18. Zhao, H.S., Zhang, Y., Lie, S.T.: Explicit frequency equations of free vibration of a nonlocal Timoshenko beam with surface effects. Acta Mech. Sin. 34, 676–688 (2018)

    Article  MathSciNet  Google Scholar 

  19. Chandrasekharaiah, D.S.: On surface waves in an elastic half-space with material boundary. Acta Mech. 41, 283–287 (1981)

    Article  Google Scholar 

  20. Krylov, V.V.: Surface properties of solids and surface acoustic waves: application to chemical sensors and layer characterization. Appl. Phys. A 61, 229–236 (1995)

    Article  Google Scholar 

  21. Eremeyev, V.A., Rosi, G., Naili, S.: Surface/interfacial anti-plane waves in solids with surface energy. Mech. Res. Commun. 74, 8–13 (2016)

    Article  Google Scholar 

  22. Eremeyev, V.A.: Strongly anisotropic surface elasticity and antiplane surface waves. Philos. Trans. R. Soc. A 378, 20190100 (2020)

    Article  MathSciNet  Google Scholar 

  23. Georgiadis, H.G., Velgaki, E.G.: High-frequency Rayleigh waves in materials with micro-structure and couple-stress effects. Int. J. Solids Struct. 40, 2501–2520 (2003)

    Article  Google Scholar 

  24. Miller, R.E., Shenoy, V.B.: Size-dependent elastic properties of nanosized structural elements. Nanotechnology 11, 139 (2000)

    Article  Google Scholar 

  25. Shenoy, V.B.: Atomistic calculations of elastic properties of metallic fcc crystal surfaces. Phys. Rev. B 71, 094104 (2005)

    Article  Google Scholar 

  26. Chen, S.H., Yao, Y.: Elastic theory of nanomaterials based on surface-energy density. J. Appl. Mech. 81, 121002 (2014)

    Article  Google Scholar 

  27. Lamber, R., Wetjen, S., Jaeger, N.I.: Size dependence of the lattice parameter of small palladium particles. Phys. Rev. B 51, 10968 (1995)

    Article  Google Scholar 

  28. Vitos, L., Ruban, A.V., Skriver, H.L., et al.: The surface energy of metals. Surf. Sci. 411, 186–202 (1998)

    Article  Google Scholar 

  29. Woltersdorf, J., Nepijko, A.S., Pippel, E.: Dependence of lattice parameters of small particles on the size of the nuclei. Surf. Sci. 106, 64–69 (1981)

    Article  Google Scholar 

  30. Zhang, C., Yao, Y., Chen, S.: Size-dependent surface energy density of typically fcc metallic nanomaterials. Comput. Mater. Sci. 82, 372–377 (2014)

    Article  Google Scholar 

  31. Wang, Y.X., Zhang, B., Zhang, X., et al.: Two-dimensional fretting contact analysis considering surface effects. Int. J. Solids Struct. 170, 68–81 (2019)

    Article  Google Scholar 

  32. Jia, N., Yao, Y., Peng, Z., et al.: Surface effect in axisymmetric Hertzian contact problems. Int. J. Solids Struct. 150, 241–254 (2018)

    Article  Google Scholar 

  33. Jia, N., Peng, Z., Yang, Y., et al.: The coupling effect of surface effect and chemical diffusion in lithium-ion battery with spherical nanoparticle electrodes. Int. J. Appl. Mech. 12, 2050091 (2020)

    Article  Google Scholar 

  34. Zhang, X., Wang, Q.J., Wang, Y.X., et al.: Contact involving a functionally graded elastic thin film and considering surface effects. Int. J. Solids Struct. 150, 184–196 (2018)

    Article  Google Scholar 

  35. Jia, N., Peng, Z., Yao, Y., et al.: A surface energy density-based theory of nanoelastic dynamics and its application in the scattering of P-wave by a cylindrical nanocavity. J. Appl. Mech. 87, 101001 (2020)

    Article  Google Scholar 

  36. Wasserman, H.J., Vermaak, J.S.: On the determination of a lattice contraction in very small silver particles. Surf. Sci. 22, 164–172 (1970)

    Article  Google Scholar 

  37. Brady, G.S., Clauser, H.R., Vaccari, J.A.: Materials Handbook (Handbook). McGraw-Hill Professional, New York (2002)

    Google Scholar 

  38. Jia, N., Yao, Y., Yang, Y., et al.: Analysis of two-dimensional contact problems considering surface effect. Int. J. Solids Struct. 125, 172–183 (2017)

    Article  Google Scholar 

  39. Mi, C., Jun, S., Kouris, D.A., et al.: Atomistic calculations of interface elastic properties in noncoherent metallic bilayers. Phys. Rev. B 77, 439–446 (2008)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants 11532013, 11872114, 11772333, and 12002033) and the Project of State Key Laboratory of Explosion Science and Technology (Grant ZDKT17-02).

Author information

Authors and Affiliations

  1. Institute of Advanced Structure Technology, Beijing Institute of Technology, Beijing, 100081, China

    Ning Jia, Zhilong Peng, Yin Yao & Shaohua Chen

  2. Beijing Key Laboratory of Lightweight Multi-Functional Composite Materials and Structures, Beijing Institute of Technology, Beijing, 100081, China

    Ning Jia, Zhilong Peng, Yin Yao & Shaohua Chen

  3. School of Mechanical and Electrical Engineering, Central South University, Changsha, 410083, China

    Jianjun Li

Authors
  1. Ning Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhilong Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jianjun Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yin Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shaohua Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Yin Yao or Shaohua Chen.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Executive Editor: Hui-Ling Duan

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jia, N., Peng, Z., Li, J. et al. Dispersive behavior of high frequency Rayleigh waves propagating on an elastic half space. Acta Mech. Sin. 37, 562–569 (2021). https://doi.org/10.1007/s10409-020-01009-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-020-01009-3

Keywords

Search

Navigation