Abstract
A new material tailoring method for spherical and cylindrical vessels made of functionally graded materials (FGMs) is presented. It is assumed that the FG material is composed of an Al–SiC metallic-matrix composite. A uniform ratio of in-plane shear stress to yield strength [\(\varphi \left( r \right) \)] is used as the design criterion to utilize the maximum capacity of the vessel. The aim is to find a distribution of SiC particles in the radial direction, i.e., \(f\left( r \right) \), that achieves a uniform index \(\varphi \left( r \right) =\hbox {const}.\) through the wall thickness of the internally pressurized spherical or cylindrical vessel. Both the Mori–Tanaka and rule-of-mixtures homogenization schemes are used to express the effective elastic module and Poisson’s ratio. Moreover, the strength of the composite is expressed based on the rule of mixtures. Besides, finite element simulation is carried out to verify the accuracy of the analytical solution. The effects of input parameters such as the internal pressure, strength of the SiC particles, ratio of in-plane shear stress to effective yield strength, and choice of homogenization scheme on the tailored distribution of the SiC volume fraction in the radial direction are also investigated.











Similar content being viewed by others
Abbreviations
- a, b :
-
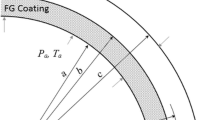
Inner and outer radius of sphere or cylinder, respectively
- u :
-
Radial displacement
- c :
-
Constant value of in-plane shear stress divided by effective yield strength
- \(f\left( r \right) \) :
-
Radial distribution of SiC particles
- \(N_1 ,\,N_2 \) :
-
Constants related to material properties based on Mori–Tanaka homogenization
- \(C_1-C_9 \) :
-
Constants related to material properties based on Mori–Tanaka homogenization
- \(Z_1-Z_9 \) :
-
Constants related to material properties based on Mori–Tanaka homogenization
- \(P_a ,P_b \) :
-
Internal and external pressure, respectively
- E :
-
Elastic modulus
- K :
-
Bulk modulus
- Y :
-
Yield strength
- \(\mu \) :
-
Shear modulus
- \(\varphi \left( r \right) \) :
-
In-plane shear stress divided by effective yield strength
- \(\varepsilon _r ,\varepsilon _\theta ,\varepsilon _\varphi \) :
-
Strains in radial, and first and second circumferential directions, respectively
- \(\sigma _r ,\sigma _\theta \) :
-
Radial and circumferential stress, respectively
- v :
-
Poisson’s ratio
- \(\mathrm {p},\,\mathrm {m}\) :
-
Subscripts denoting particle andmatrix, respectively
- MT (MTHS):
-
Subscript (abbreviation) for Mori–Tanaka homogenization scheme
- RM (RMHS):
-
Subscript (abbreviation) for rule-of-mixtures homogenization scheme
References
Loghman, A., Parsa, H.: Exact solution for magneto–thermo–elastic behaviour of double-walled cylinder made of an inner FGM and an outer homogeneous layer. Int. J. Mech. Sci. 88, 93–99 (2014)
Jha, D., Kant, T., Singh, R.: A critical review of recent research on functionally graded plates. Compos. Struct. 96, 833–849 (2013)
Rodrıguez-Castro, R., Wetherhold, R., Kelestemur, M.: Microstructure and mechanical behavior of functionally graded Al A359/SiC p composite. Mater. Sci. Eng. A 323, 445–456 (2002)
Mahmoudi, T., Parvizi, A., Poursaeidi, E., et al.: Thermo-mechanical analysis of functionally graded wheel-mounted brake disk. J. Mech. Sci. Technol. 29, 4197–4204 (2015)
Nosouhi Dehnavi, F., Parvizi, A.: Electrothermomechanical behaviors of spherical vessels with different configurations of functionally graded piezoelectric coating. J. Intel. Mat. Syst. Struct. 10.1177/1045389X17742737 (2017)
Sharma, D., Sharma, J., Dhaliwal, S., et al.: Vibration analysis of axisymmetric functionally graded viscothermoelastic spheres. Acta Mech. Sin. 30, 100–111 (2014)
Kim, Y.W.: Effect of partial elastic foundation on free vibration of fluid-filled functionally graded cylindrical shells. Acta Mech. Sin. 31, 920–930 (2015)
Dehnavi, F.N., Parvizi, A.: Investigation of thermo-elasto-plastic behavior of thick-walled spherical vessels with inner functionally graded coatings. Meccanica 52, 1–18 (2016)
Eraslan, A., Akis, T.: On the plane strain and plane stress solutions of functionally graded rotating solid shaft and solid disk problems. Acta Mech. 181, 43–63 (2006)
Ozturk, A., Gulgec, M.: Elastic-plastic stress analysis in a long functionally graded solid cylinder with fixed ends subjected to uniform heat generation. Int. J. Eng. Sci. 49, 1047–1061 (2011)
Keles, I., Conker, C.: Transient hyperbolic heat conduction in thick-walled FGM cylinders and spheres with exponentially-varying properties. Eur. J. Mech. A Sol. 30, 449–455 (2011)
Tutuncu, N.: Stresses in thick-walled FGM cylinders with exponentially-varying properties. Eng. Struct. 29, 2032–2035 (2007)
Parvizi, A., Naghdabadi, R., Arghavani, J.: Analysis of Al A359/SiCp functionally graded cylinder subjected to internal pressure and temperature gradient with elastic–plastic deformation. J. Therm. Stress. 34, 1054–1070 (2011)
Mirzaei, M., Kiani, Y.: Free vibration of functionally graded carbon nanotube reinforced composite cylindrical panels. Compos. Struct. 142, 45–56 (2016)
Xin, L., Yang, S., Zhou, D., et al.: An approximate analytical solution based on the Mori-Tanaka method for functionally graded thick-walled tube subjected to internal pressure. Compos. Struct. 135, 74–82 (2016)
Ebrahimi, F., Barati, M.R., Dabbagh, A.: A nonlocal strain gradient theory for wave propagation analysis in temperature-dependent inhomogeneous nanoplates. Int. J. Eng. Sci. 107, 169–182 (2016)
Xin, L., Dui, G., Yang, S., et al.: Solutions for behavior of a functionally graded thick-walled tube subjected to mechanical and thermal loads. Int. J. Mech. Sci. 98, 70–79 (2015)
Eslami, M., Babaei, M., Poultangari, R.: Thermal and mechanical stresses in a functionally graded thick sphere. Int. J. Press. Vessels Pip. 82, 522–527 (2005)
Jabbari, M., Sohrabpour, S., Eslami, M.R.: Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads. Int. J. Press. Vessels Pip. 79, 493–497 (2002)
Arefi, M.: Nonlinear thermoelastic analysis of thick-walled functionally graded piezoelectric cylinder. Acta Mech. 224, 2771 (2013)
You, L., Zhang, J., You, X.: Elastic analysis of internally pressurized thick-walled spherical pressure vessels of functionally graded materials. Int. J. Press. Vessels Pip. 82, 347–354 (2005)
Atashipour, S.A., Sburlati, R., Atashipour, S.R.: Elastic analysis of thick-walled pressurized spherical vessels coated with functionally graded materials. Meccanica 49, 2965–2978 (2014)
Wang, Z., Zhang, Q., Xia, L., et al.: Thermomechanical analysis of pressure vessels with functionally graded material coating. J. Press. Vessel Technol. 138, 011205 (2016)
Mohammadi, M., Saha, G.C., Akbarzadeh, A.H.: Elastic field in composite cylinders made of functionally graded coatings. Int. J. Eng. Sci. 101, 156–170 (2016)
Parvizi, A., Alikarami, S., Asgari, M.: Exact solution for thermoelastoplastic behavior of thick-walled functionally graded sphere under combined pressure and temperature gradient loading. J. Therm. Stress. 39, 1152–1170 (2016)
Alikarami, S., Parvizi, A.: Elasto–plastic analysis and finite element simulation of thick-walled functionally graded cylinder subjected to combined pressure and thermal loading. Sci. Eng. Compos. Mater. 24, 609–620 (2017)
Cho, J.R., Ha, D.Y.: Volume fraction optimization for minimizing thermal stress in Ni–Al\(_2\)O\(_3\) functionally graded materials. Mat. Sci. Eng. A 334, 147–155 (2002)
Taheri, A.H., Hassani, B., Moghaddam, N.Z.: Thermo-elastic optimization of material distribution of functionally graded structures by an isogeometrical approach. Int. J. Sol. Struct. 51, 416–429 (2014)
Nemat-Alla, M.: Reduction of thermal stresses by composition optimization of two-dimensional functionally graded materials. Acta Mech. 208, 147–161 (2009)
Zhang, X.D., Hong, Y.L.: Li, A.H.: Optimization of axial symmetrical FGM under the transient-state temperate field. Int. J. Miner. Metall. Mat. 19, 59–63 (2012)
Wang, Z.W., Zhang, Q., Xia, L.Z., et al.: Stress analysis and parameter optimization of an FGM pressure vessel subjected to thermo-mechanical loadings. Procedia Eng. 130, 374–389 (2015)
Nie, G., Batra, R.: Stress analysis and material tailoring in isotropic linear thermoelastic incompressible functionally graded rotating disks of variable thickness. Compos. Struct. 92, 720–729 (2010)
Nie, G., Batra, R.: Material tailoring and analysis of functionally graded isotropic and incompressible linear elastic hollow cylinders. Compos. Struct. 92, 265–274 (2010)
Nie, G., Zhong, Z., Batra, R.: Material tailoring for orthotropic elastic rotating disks. Compos. Sci. Technol. 71, 406–414 (2011)
Nie, G., Zhong, Z., Batra, R.: Material tailoring for functionally graded hollow cylinders and spheres. Compos. Sci. Technol. 71, 666–673 (2011)
Benveniste, Y.: A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mat. 6, 147–157 (1987)
Sadd, M.H.: Elasticity: Theory, Applications, and Numerics. Academic Press, Cambridge (2009)
Xin, L., Lu, W., Yang, S., et al.: Influence of linear work hardening on the elastic–plastic behavior of a functionally graded thick-walled tube. Acta Mech. 227, 2305–2321 (2016)
Acknowledgements
The work was supported by the Iran National Science Foundation (INSF).
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
The constants \(Z_1 -Z_9 \) in Eqs. (14) and (20) are given as follows
where \(N_1 -N_2 \) and \(C_1 -C_9 \) are \(N_1 =\frac{1}{c\left( {i+1} \right) (Y_\mathrm{p} -Y_\mathrm{m} )}\) (\(i=0\) for cylinder and \(i=1\) for sphere) and
and \(a_1-a_9 \) are
Rights and permissions
About this article
Cite this article
Nosouhi Dehnavi, F., Parvizi, A. & Abrinia, K. Novel material tailoring method for internally pressurized FG spherical and cylindrical vessels. Acta Mech. Sin. 34, 936–948 (2018). https://doi.org/10.1007/s10409-018-0772-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-018-0772-1