Skip to main content
SpringerLink
Log in

Theoretical prediction on corrugated sandwich panels under bending loads

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

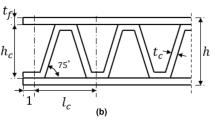
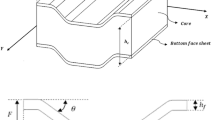
In this paper, an aluminum corrugated sandwich panel with triangular core under bending loads was investigated. Firstly, the equivalent material parameters of the triangular corrugated core layer, which could be considered as an orthotropic panel, were obtained by using Castigliano’s theorem and equivalent homogeneous model. Secondly, contributions of the corrugated core layer and two face panels were both considered to compute the equivalent material parameters of the whole structure through the classical lamination theory, and these equivalent material parameters were compared with finite element analysis solutions. Then, based on the Mindlin orthotropic plate theory, this study obtain the closed-form solutions of the displacement for a corrugated sandwich panel under bending loads in specified boundary conditions, and parameters study and comparison by the finite element method were executed simultaneously.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Wittrick, W.H.: On the local buckling of truss-type corrugated-core sandwich panels in compression. Int. J. Mech. Sci. 14, 263–264 (1972)

    Article  Google Scholar 

  2. Liu, T., Deng, Z.C., Lu, T.J.: Structural modeling of sandwich structures with lightweight cellular cores. Acta Mech. Sin. 23, 545–559 (2007)

    Article  Google Scholar 

  3. Magnucka, E., Walczak, Z., Jasion, P., et al.: Buckling and vibrations of metal sandwich beams with trapezoidal corrugated cores—the lengthwise corrugated main core. Thin Wall Struct. 112, 78–82 (2017)

    Article  Google Scholar 

  4. Hou, S.J., Zhao, S.Y., Ren, L.L., et al.: Crashworthiness optimization of corrugated sandwich panels. Mater Des. 51, 1071–1084 (2013)

    Article  Google Scholar 

  5. Liu, T.Q., Hou, S.J., Nguyen, X., et al.: Energy absorption characteristics of sandwich structures with composite sheets and bio coconut core. Compos. B. Eng. 114, 328–338 (2017)

    Article  Google Scholar 

  6. Biagi, R., Bart-Smith, H.: In-plane column response of metallic corrugated core sandwich panels. Int. J. Solids Struct. 49, 3901–3914 (2012)

    Article  Google Scholar 

  7. Rejab, M.R.M., Cantwell, W.J.: The mechanical behaviour of corrugated-core sandwich panels. Compos. Part B Eng. 47, 267–277 (2013)

    Article  Google Scholar 

  8. Yan, L.L., Han, B., Yu, B., et al.: Three-point bending of sandwich beams with aluminum foam-filled corrugated cores. Mater. Des. 60, 510–519 (2014)

    Article  Google Scholar 

  9. Chang, W.S., Ventsel, E., Krauthammer, T., et al.: Bending behavior of corrugated-core sandwich plates. Compos. Struct. 70, 81–89 (2005)

    Article  Google Scholar 

  10. Rubino, V., Deshpande, V.S., Fleck, N.A.: The three-point bending of Y-frame and corrugated core sandwich beams. Int. J. Mech. Sci. 52, 485–494 (2010)

    Article  Google Scholar 

  11. Liu, C., Zhang, Y.X., Ye, L.: High velocity impact responses of sandwich panels with metal fibre laminate skins and aluminium foam core. Int. J. Impact Eng. 100, 139–153 (2016)

    Article  Google Scholar 

  12. Qin, Q.H., Xiang, C.P., Zhang, J.X., et al.: On low-velocity impact response of metal foam core sandwich beam: a dual beam model. Compos. Struct. 176, 1039–1049 (2017)

    Article  Google Scholar 

  13. Zhang, J.X., Qin, Q.H., Xiang, C.P., et al.: Dynamic response of slender multilayer sandwich beams with metal foam cores subjected to low-velocity impact. Compos. Struct. 153, 614–623 (2016)

    Article  Google Scholar 

  14. Hou, S.J., Shu, C.F., Zhao, S.Y., et al.: Experimental and numerical studies on multi-layered corrugated sandwich panels under crushing loading. Compos. Struct. 126, 371–385 (2015)

    Article  Google Scholar 

  15. Yang, X.F., Ma, J.X., Shi, Y.L., et al.: Crashworthiness investigation of the bio-inspired bi-directionally corrugated core sandwich panel under quasi-static crushing load. Mater. Des. 135, 275–290 (2017)

    Article  Google Scholar 

  16. Liang, C.C., Yang, M.F., Wu, P.W.: Optimum design of metallic corrugated core sandwich panels subjected to blast loads. Ocean Eng. 28, 825–861 (2001)

    Article  Google Scholar 

  17. Zhang, P., Liu, J., Cheng, Y.S., et al.: Dynamic response of metallic trapezoidal corrugated-core sandwich panels subjected to air blast loading: an experimental study. Mater. Des. 65, 221–230 (2015)

    Article  Google Scholar 

  18. Yazici, M., Wright, J., Bertin, D., et al.: Experimental and numerical study of foam filled corrugated core steel sandwich structures subjected to blast loading. Compos. Struct. 110, 98–109 (2014)

    Article  Google Scholar 

  19. Libove, C., Batdorf, S.B.: A general small-deflection theory for flat sandwich plates. Tech. Rep. Arch. Image Lib. 899 (1948)

  20. Libove, C., Hubka, R.E.: Elastic constants for corrugated-core sandwich plates. J. Struct. Eng. ASCE 122, 958–966 (1951)

    Google Scholar 

  21. Briassoulis, D.: Equivalent orthotropic properties of corrugated sheets. Comput. Struct. 23, 129–138 (1986)

    Article  Google Scholar 

  22. Bartolozzi, G., Pierini, M., Orrenius, U., et al.: An equivalent material formulation for sinusoidal corrugated cores of structural sandwich panels. Compos. Struct. 100, 173–185 (2013)

    Article  Google Scholar 

  23. Bartolozzi, G., Baldanzini, N., Pierini, M.: Equivalent properties for corrugated cores of sandwich structures: a general analytical method. Compos. Struct. 108, 736–746 (2014)

    Article  Google Scholar 

  24. Xia, Y., Friswell, M.I., Flores, E.I.: Equivalent models of corrugated panels. Int. J. Solids Struct. 49, 1453–1462 (2012)

    Article  Google Scholar 

  25. Ye, Z., Berdichevsky, V.L., Yu, W.: An equivalent classical plate model of corrugated structures. Int. J. Solids Struct. 51, 2073–2083 (2014)

    Article  Google Scholar 

  26. Romanoff, J., Varsta, P.: Bending response of web-core sandwich plates. Compos. Struct. 81, 292–302 (2007)

    Article  Google Scholar 

  27. Åslund, P.E., Hägglund, R., Carlsson, L.A., et al.: An analysis of strain localization and formation of face wrinkles in edge-wise loaded corrugated sandwich panels using a continuum damage model. Int. J. Solids Struct. 56–57, 248–257 (2014)

    Google Scholar 

  28. Castigliano, C.A.: Intorno ai sistemi elastici. Thesis, University of Turin (1873)

  29. Nilson, A.H., Ammar, A.R.: Finite element analysis of metal deck shear diaphragms. J. Struct. Div. 100, 711–726 (1974)

    Google Scholar 

  30. Mindlin, R.D.: Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates. J. Appl. Mech. 18, 31–38 (1951)

    MATH  Google Scholar 

Download references

Acknowledgements

The financial support from the National Natural Science Foundation of China (Grant 11572122) is acknowledged. Meanwhile, the Scientific Research Foundation of Huaihua University (Grant HHUY2017-02), 111 Project (Grant B16015), Stake Key Laboratory of Mechanical Structural Strength and Vibration (Grant SV2017-KF-20) and Joint Centre for Intelligent New Energy Vehicle are also acknowledged.

Author information

Authors and Affiliations

  1. College of Mechanical and Optoelectronics Physics, Huaihua University, Huaihua, 418008, China

    Chengfu Shu

  2. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha, 410082, China

    Chengfu Shu & Shujuan Hou

  3. College of Mechanical and Vehicle Engineering, Hunan University, Changsha, 410082, China

    Shujuan Hou

Authors
  1. Chengfu Shu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shujuan Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shujuan Hou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shu, C., Hou, S. Theoretical prediction on corrugated sandwich panels under bending loads. Acta Mech. Sin. 34, 925–935 (2018). https://doi.org/10.1007/s10409-018-0767-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-018-0767-y

Keywords

Search

Navigation