Skip to main content
SpringerLink
Log in

Macroscopic damping model for structural dynamics with random polycrystalline configurations

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

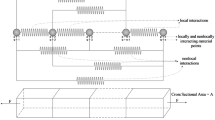
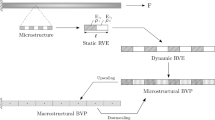
In this paper the macroscopic damping model for dynamical behavior of the structures with random polycrystalline configurations at micro–nano scales is established. First, the global motion equation of a crystal is decomposed into a set of motion equations with independent single degree of freedom (SDOF) along normal discrete modes, and then damping behavior is introduced into each SDOF motion. Through the interpolation of discrete modes, the continuous representation of damping effects for the crystal is obtained. Second, from energy conservation law the expression of the damping coefficient is derived, and the approximate formula of damping coefficient is given. Next, the continuous damping coefficient for polycrystalline cluster is expressed, the continuous dynamical equation with damping term is obtained, and then the concrete damping coefficients for a polycrystalline Cu sample are shown. Finally, by using statistical two-scale homogenization method, the macroscopic homogenized dynamical equation containing damping term for the structures with random polycrystalline configurations at micro–nano scales is set up.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

(Source: “Microstructure of VT22 (Ti5Al5Mo5V1,5Cr) after quenching” by Edward Pleshakov, used under the CC BY-SA 3.0 license)

Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Bower, A.F.: Applied Mechanics of Solids. CRC Press, Boca Raton (2009)

    Google Scholar 

  2. Tadmor, E.B., Miller, R.E.: Modeling Materials. Continuum, Atomistic and Multiscale Techniques. Cambridge University Press, Cambridge (2011)

    Book  MATH  Google Scholar 

  3. Wilson, E.L.: Three Dimensional Static and Dynamic Analysis of Structures. Computers and Structures Inc, Berkeley (2000)

    Google Scholar 

  4. Clough, R.W., Penzien, J.: Dynamics of Structures. McGraw-Hill College, New York (1975)

    MATH  Google Scholar 

  5. Chopra, A.K.: Dynamics of Structures. Pearson, Upper Saddle River (2016)

    Google Scholar 

  6. Williams, M.: Structural Dynamics. CRC Press, Boca Raton (2016)

    Google Scholar 

  7. Li, B., Cui, J., Tian, X., et al.: The calculation of mechanical behavior for metallic devices at nano-scale based on Atomic–Continuum Coupled model. Comput. Mater. Sci. 94, 73–84 (2014)

    Article  Google Scholar 

  8. Aurenhammer, F., Klein, R., Lee, D.T.: Voronoi Diagrams and Delaunay Triangulations. World Scientific Publishing Co Inc, Singapore (2013)

    Book  MATH  Google Scholar 

  9. Okabe, A., Boots, B., Sugihara, K., et al.: Spatial Tessellations. Concepts and Applications of Voronoi Diagrams. Wiley, New York (2009)

    MATH  Google Scholar 

  10. Plimpton, S.: Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995)

    Article  MATH  Google Scholar 

  11. Foiles, S.M., Baskes, M.I., Daw, M.S.: Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B 33, 7983–7991 (1986)

    Article  Google Scholar 

  12. Thijssen, J.: Computational Physics. Cambridge University Press, Cambridge (2007)

    Book  MATH  Google Scholar 

  13. Frenkel, D., Smit, B.: Understanding Molecular Simulation. From Algorithms to Applications. Academic Press, San Diego (2001)

    MATH  Google Scholar 

  14. Israelachvili, J.N.: Intermolecular and Surface Forces. Academic Press, San Diego (2015)

    Google Scholar 

  15. Xiang, M., Cui, J., Li, B., et al.: Atom-continuum coupled model for thermo-mechanical behavior of materials in micro–nano scales. Sci. China Phys. Mech. Astron. 55, 1125–1137 (2012)

    Article  Google Scholar 

  16. Han, T., Cui, J., Yu, X., et al.: A local Quantum–Atomistic–Continuum model for mechanical behaviors at micro–nano scale. Comput. Mater. Sci. 109, 312–322 (2015)

    Article  Google Scholar 

  17. Yang, Y., Cui, J., Han, T.: Error analysis for momentum conservation in Atomic–Continuum Coupled Model. Comput. Mech. 58, 199–211 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Han, T.: A local Quantum–Atomistic–Continuum model for mechanical behaviors of micro–nano materials and components. [Ph.D. Thesis], University of Chinese Academy of Sciences, China (2016)

  19. Cioranescu, D., Donato, P.: An Introduction to Homogenization. Oxford University Press, Oxford (1999)

    MATH  Google Scholar 

  20. Pavliotis, G.A., Stuart, A.: Multiscale Methods. Averaging and Homogenization. Springer, New York (2008)

    MATH  Google Scholar 

  21. Wan, J.: Multi-scale analysis method for dynamic coupled thermoelasticity of composite structures. [Ph.D. Thesis], University of Chinese Academy of Sciences, China (2007)

  22. Grinfeld, P.: Introduction to Tensor Analysis and the Calculus of Moving Surfaces. Springer, New York (2013)

    Book  MATH  Google Scholar 

  23. Yang, Z.: The second-order two-scale method for predicting dynamic thermo-mechanical performance of random composite materials. [Ph.D. Thesis], Northwestern Polytechnical University, China (2014)

  24. Yang, Z., Cui, J.: The statistical second-order two-scale analysis for dynamic thermo-mechanical performances of the composite structure with consistent random distribution of particles. Comput. Mater. Sci. 69, 359–373 (2013)

    Article  Google Scholar 

  25. Ross, S.: A First Course in Probability. Pearson, Upper Saddle River (2015)

    MATH  Google Scholar 

Download references

Acknowledgements

This work was partially supported by the National Basic Research Program of China (973 Program Grant 2012CB025904), the National Natural Science Foundation of China (Grant 11102221), and the State Key Laboratory of Science and Engineering Computing (LSEC).

Author information

Authors and Affiliations

  1. Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Yantao Yang, Junzhi Cui & Yifan Yu

  2. Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing, 100088, China

    Meizhen Xiang

Authors
  1. Yantao Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junzhi Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yifan Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Meizhen Xiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Junzhi Cui.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Y., Cui, J., Yu, Y. et al. Macroscopic damping model for structural dynamics with random polycrystalline configurations. Acta Mech. Sin. 34, 493–506 (2018). https://doi.org/10.1007/s10409-017-0733-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-017-0733-0

Keywords

Search

Navigation