SIF-based fracture criterion for interface cracks

Abstract

The complex stress intensity factor K governing the stress field of an interface crack tip may be split into two parts, i.e., $\hat{K}$ and $s^{-\mathrm{i}\varepsilon }$, so that $K=\hat{K}s^{-\mathrm{i}\varepsilon }, s$ is a characteristic length and $\varepsilon$ is the oscillatory index. $\hat{K}$ has the same dimension as the classical stress intensity factor and characterizes the interface crack tip field. That means a criterion for interface cracks may be formulated directly with $\hat{K}$, as Irwin (ASME J. Appl. Mech. 24:361–364, 1957) did in 1957 for the classical fracture mechanics. Then, for an interface crack, it is demonstrated that the quasi Mode I and Mode II tip fields can be defined and distinguished from the coupled mode tip fields. Built upon SIF-based fracture criteria for quasi Mode I and Mode II, the stress intensity factor (SIF)-based fracture criterion for mixed mode interface cracks is proposed and validated against existing experimental results.

Appendices

Appendix 1

The criterion for mixed mode based on the energy release rate for an interface crack is

$$\begin{aligned} \left( {\frac{G_\mathrm{I} }{G_\mathrm{IC} }} \right) +\left( {\frac{G_\mathrm{II}}{G_\mathrm{IIC} }} \right) =1, \end{aligned}$$

(35)

therefore,

$$\begin{aligned} G_\mathrm{I} =G_\mathrm{IC} - G_\mathrm{IC} \frac{G_\mathrm{II}}{G_\mathrm{IIC}}. \end{aligned}$$

(36)

Since

$$\begin{aligned} \tan \hat{\psi }=\frac{\hat{K}_\mathrm{QII}}{\hat{K}_\mathrm{QI}}, \end{aligned}$$

(37)

we have

$$\begin{aligned} \tan ^{2}\hat{\psi }=\frac{G_\mathrm{II}}{G_\mathrm{I}}, \end{aligned}$$

(38)

and

$$\begin{aligned} G\left( {\hat{\psi }} \right) =G_\mathrm{I} +G_\mathrm{II} =G_\mathrm{I} \left( {1+\tan ^{2}\hat{\psi }} \right) . \end{aligned}$$

(39)

Substitute Eq. (36) into Eq. (39),

$$\begin{aligned} G\left( {\hat{\psi }} \right) =G_\mathrm{IC} \left( {1-\frac{G_\mathrm{II} }{G_\mathrm{IIC} }} \right) \left( {1+\tan ^{2}\hat{\psi }} \right) , \end{aligned}$$

(40)

then, Eq. (40) may be simplified to the criterion based on the energy release rate as follows,

$$\begin{aligned} G\left( {\hat{\psi }} \right) =\frac{G_\mathrm{IC} \left( {1+\tan ^{2}\hat{\psi }} \right) }{1+(G_{\mathrm{IC}} /G_{\mathrm{IIC}} )\tan ^{2}\hat{\psi }}. \end{aligned}$$

(41)

Appendix 2

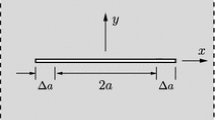
In addition, Liechti and Chai [13] measured the critical interface toughness with a plane strain specimen as showed in the insert of Fig. 1. The problem associated with the interface crack in this specimen has been solved analytically by Rice [14]. The solution is

$$\begin{aligned}&K_1 +\mathrm{i}K_2\nonumber \\&\quad =\frac{\sqrt{2}\mu _1 \mu _2 h^{-1/{2-\mathrm{i}\varepsilon }}\mathrm{e}^{\mathrm{i}\omega }\left( {cV+\mathrm{i}U} \right) }{\left( {1-\beta ^{2}} \right) ^{1/2}\left( {\mu _1 +\mu _2 } \right) ^{1/2}\left[ {\mu _1 \left( {1-\nu _2 } \right) +\mu _2 \left( {1-\nu _1 } \right) } \right] ^{1/2}},\nonumber \\ \end{aligned}$$

(42)

where

$$\begin{aligned} c=\left\{ {\frac{2\left( {\mu _1 +\mu _2 } \right) }{\mu _1 \left[ {{\left( {1-2\nu _2 } \right) }/{\left( {1-\nu _2 } \right) }} \right] +\mu _2 \left[ {{\left( {1-2\nu _1 } \right) }/{\left( {1-\nu _1 } \right) }} \right] }} \right\} ,\nonumber \\ \end{aligned}$$

(43)

for this specimen system, $\omega =16^{\circ }$ and $\varepsilon =0.06$.

The phase angle $\psi$ is defined as

$$\begin{aligned} \psi =\tan ^{-1}\left[ {\frac{\hbox {Im}\left( {Kl^{\mathrm{i}\varepsilon }} \right) }{\hbox {Re}\left( {Kl^{\mathrm{i}\varepsilon }} \right) }} \right] , \end{aligned}$$

(44)

where

$$\begin{aligned} Kl^{\mathrm{i}\varepsilon }=\frac{\sqrt{2}\mu _1 \mu _2 h^{-1/2}\left( {l/h} \right) ^{\mathrm{i}\varepsilon }\mathrm{e}^{\mathrm{i}\omega }\left( {cV+\mathrm{i}U} \right) }{\left( {1-\beta ^{2}} \right) ^{1/2}\left( {\mu _1 +\mu _2 } \right) ^{1/2}\left[ {\mu _1 \left( {1-\nu _2 } \right) +\mu _2 \left( {1-\nu _1 } \right) } \right] ^{1/2}}.\nonumber \\ \end{aligned}$$

(45)

The phase angle $\psi$ is given in Sect. 4 of Ref. [7], as

$$\begin{aligned} \psi =\gamma +\omega +\varepsilon \ln \left( {l/h} \right) , \end{aligned}$$

(46)

where

$$\begin{aligned} \gamma =\tan ^{-1}\left[ {U/{(cV)}} \right] . \end{aligned}$$

(47)

In the present paper,

$$\begin{aligned} \hat{K}_\mathrm{QI}= & {} \frac{\sqrt{2}\mu _1 \mu _2 h^{-1/2}\left( {cV} \right) \hbox {Re}\left( {\mathrm{e}^{\mathrm{i}\omega }} \right) }{\left( {1-\beta ^{2}} \right) ^{1/2}\left( {\mu _1 +\mu _2 } \right) ^{1/2}\left[ {\mu _1 \left( {1-\nu _2 } \right) +\mu _2 \left( {1-\nu _1 } \right) } \right] ^{1/2}},\end{aligned}$$

(48)

$$\begin{aligned} \hat{K}_\mathrm{QII}= & {} \frac{\sqrt{2}\mu _1 \mu _2 h^{-1/2}\left( U \right) \hbox {Im}\left( {\mathrm{e}^{\mathrm{i}\omega }} \right) }{\left( {1-\beta ^{2}} \right) ^{1/2}\left( {\mu _1 +\mu _2 } \right) ^{1/2}\left[ {\mu _1 \left( {1-\nu _2 } \right) +\mu _2 \left( {1-\nu _1 } \right) } \right] ^{1/2}},\nonumber \\ \end{aligned}$$

(49)

and the phase angle $\hat{\psi }$ is defined as

$$\begin{aligned} \hat{\psi }=\tan ^{-1}\left( {\frac{\hat{K}_\mathrm{QII} }{\hat{K}_\mathrm{QI} }} \right) . \end{aligned}$$

(50)

From Eqs. (49)–(51), we have

$$\begin{aligned} \hat{\psi }=\gamma +\omega . \end{aligned}$$

(51)

It follows that

$$\begin{aligned} \hat{\psi }=\psi -\varepsilon \ln \left( {l/h} \right) . \end{aligned}$$

(52)