Skip to main content
SpringerLink
Log in

Steady-state responses of a belt-drive dynamical system under dual excitations

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

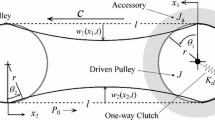
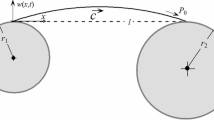
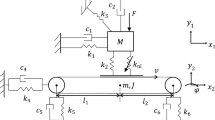
The stable steady-state periodic responses of a belt-drive system with a one-way clutch are studied. For the first time, the dynamical system is investigated under dual excitations. The system is simultaneously excited by the firing pulsations of the engine and the harmonic motion of the foundation. Nonlinear discrete–continuous equations are derived for coupling the transverse vibration of the belt spans and the rotations of the driving and driven pulleys and the accessory pulley. The nonlinear dynamics is studied under equal and multiple relations between the frequency of the firing pulsations and the frequency of the foundation motion. Furthermore, translating belt spans are modeled as axially moving strings. A set of nonlinear piecewise ordinary differential equations is achieved by using the Galerkin truncation. Under various relations between the excitation frequencies, the time histories of the dynamical system are numerically simulated based on the time discretization method. Furthermore, the stable steady-state periodic response curves are calculated based on the frequency sweep. Moreover, the convergence of the Galerkin truncation is examined. Numerical results demonstrate that the one-way clutch reduces the resonance amplitude of the rotations of the driven pulley and the accessory pulley. On the other hand, numerical examples prove that the resonance areas of the belt spans are decreased by eliminating the torque-transmitting in the opposite direction. With the increasing amplitude of the foundation excitation, the damping effect of the one-way clutch will be reduced. Furthermore, as the amplitude of the firing pulsations of the engine increases, the jumping phenomena in steady-state response curves of the belt-drive system with or without a one-way clutch both occur.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Ulsoy, A.G., Whitsell, J.E., Hooven, M.D.: Design of belt-tensioner systems for dynamic stability. J. Vib. Acoust. 107, 282–290 (1985)

    Article  Google Scholar 

  2. Chen, L.Q.: Analysis and control of transverse vibrations of axially moving strings. Appl. Mech. Rev. 58, 91–116 (2005)

    Article  Google Scholar 

  3. Marynowski, K., Kapitaniak, T.: Dynamics of axially moving continua. Int. J. Mech. Sci. 81, 26–41 (2014)

    Article  Google Scholar 

  4. Chen, L.Q., Yang, X.D.: Steady-state response of axially moving viscoelastic beams with pulsating speed: comparison of two nonlinear models. Int. J. Solids Struct. 42, 37–50 (2005)

    Article  MATH  Google Scholar 

  5. Chen, L.Q., Yang, X.D.: Stability in parametric resonance of an axially moving viscoelastic beam with time-dependent velocity. J. Sound Vib. 284, 879–891 (2005)

    Article  Google Scholar 

  6. Mote, C.D., Wu, W.Z.: Vibration coupling in continuous belt and band systems. J. Sound Vib. 102, 1–9 (1985)

    Article  Google Scholar 

  7. Michon, G., Manin, L., Parker, R.G., et al.: Duffing oscillator with parametric excitation: analytical and experimental investigation on a belt-pulley system. J. Comput. Nonlinear Dyn. 3, 031001 (2008)

    Article  Google Scholar 

  8. Zhang, L., Zu, J.W.: One-to-one auto-parametric resonance in serpentine belt drive systems. J. Sound Vib. 232, 783–806 (2000)

    Article  Google Scholar 

  9. Ding, H., Chen, L.Q.: Approximate and numerical analysis of nonlinear forced vibration of axially moving viscoelastic beams. Acta Mech. Sin. 27, 426–437 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Yao, M.H., Zhang, W., Zu, J.W.: Multi-pulse chaotic dynamics in non-planar motion of parametrically excited viscoelastic moving belt. J. Sound Vib. 331, 2624–2653 (2012)

    Article  Google Scholar 

  11. Özhan, B.B., Pakdemirli, M.: A general solution procedure for the forced vibrations of a system with cubic nonlinearities: three-to-one internal resonances with external excitation. J. Sound Vib. 329, 2603–2615 (2010)

    Article  Google Scholar 

  12. Sze, K.Y., Chen, S.H., Huang, J.L.: The incremental harmonic balance method for nonlinear vibration of axially moving beams. J. Sound Vib. 281, 611–626 (2005)

    Article  Google Scholar 

  13. Yan, Q.Y., Ding, H., Chen, L.Q.: Periodic responses and chaos behaviors of an axially accelerating viscoelastic Timoshenko beam. Nonlinear Dyn. 78, 1577–1591 (2014)

    Article  MathSciNet  Google Scholar 

  14. Ding, H., Zhang, G.C., Chen, L.Q., et al.: Forced vibrations of supercritically transporting viscoelastic beams. ASME J. Vib. Acoust. 134, 051007 (2012)

    Article  Google Scholar 

  15. Yang, X.D., Zhang, W.: Nonlinear dynamics of axially moving beam with coupled longitudinal-transversal vibrations. Nonlinear Dyn. 78, 2547–2556 (2014)

    Article  Google Scholar 

  16. Ding, H., Zu, W.J.: Periodic and chaotic responses of an axially accelerating viscoelastic beam under two-frequency excitations. Int. J. Appl. Mech. 5, 1350019 (2013)

    Article  Google Scholar 

  17. Yan, Q.Y., Ding, H., Chen, L.Q.: Nonlinear dynamics of an axially moving viscoelastic Timoshenko beam under parametric and external excitations. Appl. Math. Mech. (Engl. Ed.) (2015). doi:10.1007/s10483-015-1960-7

  18. Vernay, P., Ferraris, G., Delbez, A., et al.: Transient behaviour of a sprag-type over-running clutch: an experimental study. J. Sound Vib. 248, 567–572 (2001)

  19. Lewicki, D.G., DeSmidt, H., Smith, E.C., et al.: Dynamics of a dual-clutch gearbox system: analysis and experimental validation. J. Am. Helicopter Soc. 58, 17–28 (2013)

  20. Leamy, M.J., Wasfy, T.M.: Transient and steady-state dynamic finite element modeling of belt-drives. ASME J. Dyn. Syst. Meas. Control 124, 575–581 (2002)

  21. Zhu, F., Parker, R.G.: Non-linear dynamics of a one-way clutch in belt-pulley systems. J. Sound Vib. 279, 285–308 (2005)

    Article  Google Scholar 

  22. Zhu, F., Parker, R.G.: Perturbation analysis of a clearance-type nonlinear system. J. Sound Vib. 292, 969–979 (2006)

    Article  Google Scholar 

  23. Mockensturm, E.M., Balaji, R.: Piece-wise linear dynamic systems with one-way clutches. ASME J. Vib. Acoust. 127, 475–482 (2005)

    Article  Google Scholar 

  24. Cheon, G.J.: Nonlinear behavior analysis of spur gear pairs with a one-way clutch. J. Sound Vib. 304, 18–30 (2007)

    Article  Google Scholar 

  25. Zhu, F., Parker, R.G.: Piece-wise linear dynamic analysis of serpentine belt drives with a one-way clutch. Proc. Inst. Mech. Eng. Part C 222, 1165 (2008)

    Article  Google Scholar 

  26. Ding, H., Zu, W.J.: Effect of one-way clutch on the nonlinear vibration of belt-driven systems with a continuous belt model. J. Sound Vib. 332, 6472–6487 (2013)

    Article  Google Scholar 

  27. Ding, H., Zu, W.J.: Steady-state responses of pulley-belt systems with a one-way clutch and belt bending stiffness. ASME J. Vib. Acoust. 136, 041006 (2014)

    Article  Google Scholar 

  28. Ding, H., Li, D.P.: Static and dynamic behaviors of belt-drive dynamical systems with a one-way clutch. Nonlinear Dyn. 78, 1553–1575 (2014)

    Article  MathSciNet  Google Scholar 

  29. Beikmann, R.S., Perkins, N.C., Ulsoy, A.G.: Free vibration of serpentine belt drive systems. ASME J. Vib. Acoust. 118, 406–413 (1996)

    Article  Google Scholar 

  30. Li, X.J., Chen, L.Q.: Modal analysis of coupled vibration of belt drive systems. Appl. Math. Mech. (Engl. Ed.) 29, 9–13 (2008)

    Article  MATH  Google Scholar 

  31. Ke, L.L., Wang, Y.S., Yang, J., et al.: Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech. Sin. 30, 516–525 (2014)

    Article  MathSciNet  Google Scholar 

  32. Yang, Y., Ding, H., Chen, L.Q.: Dynamic response to a moving load of a Timoshenko beam resting on a nonlinear viscoelastic foundation. Acta Mech. Sin. 29, 718–727 (2013)

    Article  MathSciNet  Google Scholar 

  33. Chen, L.Q., Zhang, Y.L.: Multi-scale analysis on nonlinear gyroscopic systems with multi-degree-of-freedoms. J. Sound Vib. 333, 4711–4723 (2014)

    Article  Google Scholar 

  34. Zhang, J.R., Rachid, A., Zhang, Y.: Attitude control for part actuator failure of agile small satellite. Acta Mech. Sin. 24, 463–468 (2008)

    Article  MATH  Google Scholar 

  35. Leamy, M.J.: On a perturbation method for the analysis of unsteady belt-drive operation. ASME J. Appl. Mech. 72, 570–580 (2005)

    Article  MATH  Google Scholar 

  36. Čepon, G., Boltezar, M.: Dynamics of a belt-drive system using a linear complementarity problem for the belt-pulley contact description. J. Sound Vib. 319, 1019–1035 (2009)

    Article  Google Scholar 

  37. Chen, L.Q., Jiang, W.A.: A piezoelectric energy harvester based on internal resonance. Acta Mech. Sin. 31, 223–228 (2015)

    Article  MathSciNet  Google Scholar 

  38. Yang, S.P., Li, S.H., Lu, Y.J.: Investigation on dynamical interaction between a heavy vehicle and road pavement. Veh. Syst. Dyn. 48, 923–944 (2010)

    Article  Google Scholar 

Download references

Acknowledgments

The project was supported by the State Key Program of the National Natural Science Foundation of China (Grant 11232009) and the National Natural Science Foundation of China (Grants 11372171, 11422214).

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai, 200072, China

    Hu Ding

Authors
  1. Hu Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hu Ding.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ding, H. Steady-state responses of a belt-drive dynamical system under dual excitations. Acta Mech. Sin. 32, 156–169 (2016). https://doi.org/10.1007/s10409-015-0510-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-015-0510-x

Keywords

Search

Navigation