Abstract
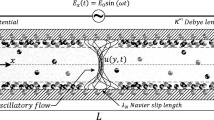
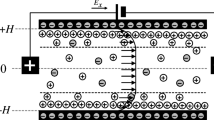
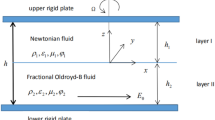
By method of the Laplace transform, this article presents semi-analytical solutions for transient electroosmotic and pressure-driven flows (EOF/PDF) of two-layer fluids between microparallel plates. The linearized Poisson-Boltzmann equation and the Cauchy momentum equation have been solved in this article. At the interface, the Maxwell stress is included as the boundary condition. By numerical computations of the inverse Laplace transform, the effects of dielectric constant ratio ɛ, density ratio ρ, pressure ratio p, viscosity ratio µ of layer II to layer I, interface zeta potential difference \(\Delta \bar \psi\), interface charge density jump Q, the ratios of maximum electro-osmotic velocity to pressure velocity α, and the normalized pressure gradient B on transient velocity amplitude are presented. We find the velocity amplitude becomes large with the interface zeta potential difference and becomes small with the increase of the viscosity. The velocity will be large with the increases of dielectric constant ratio; the density ratio almost does not influence the EOF velocity. Larger interface charge density jump leads to a strong jump of velocity at the interface. Additionally, the effects of the thickness of fluid layers (h 1 and h 2) and pressure gradient on the velocity are also investigated.
Similar content being viewed by others
References
Stone, H.A., Stroock, A.D., Ajdari, A.: Engineering flows in small devices: Microfluidics toward a Lab-on-a-chip. Annual Review of Fluid Mechanics 36, 381–411 (2004)
Bayraktar, T., Pidugu, S.B.: Characterization of liquid flows in microfluidic systems. International Journal of Heat Mass Transfer 49, 815–824 (2006)
Squires, T.M., Quake, S.R.: Microfluidics: Fluid physics at the nanoliter scale. Reviews of Modern Physics 77, 977–1026 (2005)
Hunter, R.J.: Zeta Potential in Colloid Science, Academic, San Diego (1981)
Dutta, P., Beskok, A.: Analytical solution of time periodic electro-osmotic flows: Analogies to Stokes’ second problem. Analytical Chemistry 73, 5097–5102 (2001)
Keh, H.J., Tseng, H.C.: Transient electrokinetic flow in fine capillaries. Journal Colloid Interface Science 242, 450–459 (2001)
Kang, Y.J., Yang, C., Huang, X.Y.: Dynamic aspects of electroosmotic flow in a cylindrical micro-capillary. International Journal of Engineering Science 40, 2203–2221 (2002)
Wang, X.M., Chen, B., Wu, J.K.: A semi-analytical solution of periodical electro-osmosis in a rectangular microchannel. Physics of Fluids 19, 127101 (2007)
Jian, Y.J., Yang, L.G., Liu, Q.S.: Time periodic electro-osmotic flow through a microannulus. Physics of Fluids 22, 042001 (2010)
Jian, Y.J., Liu, Q.S., Yang, L.G.: AC electro-osmotic flow of generalized Maxwell fluids in a rectangular microchannel. Journal Non-Newtonian fluid Mechanics 166, 1304–1314 (2011)
Liu, Q.S., Jian, Y.J., Yang, L.G.: Time periodic electro-osmotic flow of the generalized Maxwell fluids between two microparallel plates. Journal Non-Newtonian Fluid Mechanics 166, 478–486 (2011)
Deng, S.Y., Jian, Y.J., Bi, Y.H., et al.: Unsteady electro-osmotic flow of power-law fluid in a rectangular microchannel. Mechanics Research Communications 39, 9–14 (2010)
Su, J., Jian, Y.J., Chang, L.: Thermally fully developed electroosmotic flow through a rectangular microchannel. International Journal of Heat and Mass Transfer 55, 6285–6290 (2012)
Brask, A., Goranovic, G., Bruus, H.: Electroosmotic pumping for nonconducting liquid by viscous drag from a secondary conducting liquid, Proceedings of the Nano Tech. USA: San Francisco 1, 190–193 (2003)
Gao, Y., Wong, T.N., Yang, C., et al.: Two-fluid electro-osmotic flow in microchannels. Journal of Colloid and Interface Science 284, 306–314 (2005)
Ngoma, G.D., Erchiqui, F.: Pressure gradient and electroosmotic effects on two immiscible fluids in a microchannel between two parallel plates. Journal of Micromechanics and Microengineering 16, 83–91 (2006)
Verma, R., Sharma, A., Kargupta, K., et al.: Electric field induced instability and pattern formation in thin liquid films. Langmuir 21, 3710–3721 (2005)
Shankar, V., Sharma, A.: Instability of the interface between thin fluid films subjected to electric fields. Journal of Colloid and Interface Science 274, 294–308 (2004)
Gao Y.D., Wong T.N., Yang C., et al.: Transient two-liquid electro-osmotic flow with electric charges at the interface. Colloids and Surfaces A: Physicochem. Eng. Aspects 266, 117–128 (2005)
Liu, M., Liu, Y., Guo, Q., et al.: Modeling of electro-osmotic pumping of nonconducting liquids and biofluids by a two-phase flow method. Journal of Electroanalytical Chemistry 636, 86–92 (2009)
De Hoog, F.R., Knight, J.H., Stokes, A.N.: An improved method for numerical inversion of Laplace transforms. SIAM Journal Scientific and Statistical Computing 3, 357–366 (1982)
Author information
Authors and Affiliations
Corresponding author
Additional information
The project was supported by the National Natural Science Foundation of China (11062005 and 11202092), Open Fund of State Key Laboratory of Nonlinear Mechanics, the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region(NJYT-13-A02), the Natural Science Foundation of Inner Mongolia (2010BS0107 and 2012MS0107), the Research Start Up Fund for Excellent Talents at Inner Mongolia University (Z20080211), the support of Natural Science Key Fund of Inner Mongolia (2009ZD01), the Postgraduate Scientific Research Innovation Project of Inner Mongolia and the Enhancing Comprehensive Strength Project of Inner Mongolia University (14020202).
Rights and permissions
About this article
Cite this article
Su, J., Jian, YJ., Chang, L. et al. Transient electro-osmotic and pressure driven flows of two-layer fluids through a slit microchannel. Acta Mech Sin 29, 534–542 (2013). https://doi.org/10.1007/s10409-013-0051-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-013-0051-0