Skip to main content
SpringerLink
Log in

Novel implementation of homogenization method to predict effective properties of periodic materials

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

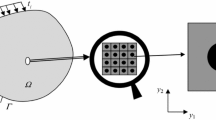
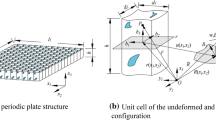
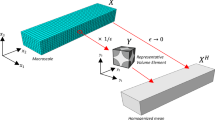
Representative volume element (RVE) method and asymptotic homogenization (AH) method are two widely used methods in predicting effective properties of periodic materials. This paper develops a novel implementation of the AH method, which has rigorous mathematical foundation of the AH method, and also simplicity as the RVE method. This implementation can be easily realized using commercial software as a black box, and can use all kinds of elements available in commercial software to model unit cells with rather complicated microstructures, so the model may remain a fairly small scale. Several examples were carried out to demonstrate the simplicity and effectiveness of the new implementation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hill, R.: A self-consistent mechanics of composite materials. Journal of the Mechanics and Physics of Solids 13, 213–222 (1965)

    Article  Google Scholar 

  2. Christensen, R.M., Lo, K.H.: Solutions for effective shear properties in three phase sphere and cylinder models. Journal of the Mechanics and Physics of Solids 27, 315–330 (1979)

    Article  MATH  Google Scholar 

  3. Kanit, T., Forest, S., Galliet, I., et al.: Determination of the size of the representative volume element for random composites: statistical and numerical approach. International Journal of Solids and Structures 40, 3647–3679 (2003)

    Article  MATH  Google Scholar 

  4. Hill, R.: The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society. Section A 65, 349–354 (1952)

    Article  Google Scholar 

  5. Yan, J., Cheng, G.D., Liu, S.T., et al.: Comparison of prediction on effective elastic property and shape optimization of truss material with periodic microstructure. International Journal of Mechanical Sciences 48, 400–413 (2006)

    Article  MATH  Google Scholar 

  6. Voigt, W.: On the relation between the elasticity constants of isotropic bodies. Ann. Phys. Chem. 274, 573–587 (1889)

    Article  Google Scholar 

  7. Reuss, A.: Determination of the yield point of polycrystals based on the yield condition of sigle crystals. Z. Angew. Math. Mech. 9, 49–58 (1929)

    Article  MATH  Google Scholar 

  8. Bakhvalov, N., Panasenko, G.: Homogenisation: Averaging Process in Periodic Media. Kluwer Academic Publ, Dordrecht (1989)

    Book  MATH  Google Scholar 

  9. Bensoussan, A., Lions, J.L., Papanicolaou, G.: Asymptotic Analysis for Periodic Structures. North Holland Publ, Amsterdam (1978)

    MATH  Google Scholar 

  10. Sanchez-Palencia, E., Zaoui, A.: Homogenization Techniques for Composite Media. Springer Verlag, Berlin (1987)

    Book  MATH  Google Scholar 

  11. Bendsøe, M.P., Kikuchi, N.: Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering 71, 197–224 (1988)

    Article  MathSciNet  Google Scholar 

  12. Fujii, D., Chen, B.C., Kikuchi, N.: Composite material design of two-dimensional structures using the homogenization design method. International Journal for Numerical Methods in Engineering 50, 2031–2051 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  13. Nishiwaki, S., Frecker, M.I., Min, S., et al.: Topology optimization of compliant mechanisms using the homogenization method. International Journal for Numerical Methods in Engineering 42, 535–559 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  14. Qiao, P., Fan, W., Davalos, J.F., et al.: Optimization of transverse shear moduli for composite honeycomb cores. Composite Structures 85, 265–274 (2008)

    Article  Google Scholar 

  15. Sigmund, O., Torquato, S.: Design of smart composite materials using topology optimization. Smart Materials and Structures 8, 365–379 (1999)

    Article  Google Scholar 

  16. Sigmund, O.: Materials with prescribed constitutive parameters: an inverse homogenization problem. International Journal of Solids and Structures 31, 2313–2329 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  17. Hassani, B., Hinton, E.: A review of homogenization and topology optimization I-homogenization theory for media with periodic structure. Computers and Structures 69, 707–717 (1998)

    Article  MATH  Google Scholar 

  18. Hassani, B., Hinton, E.: A review of homogenization and topology opimization II-analytical and numerical solution of homogenization equations. Computers and Structures 69, 719–738 (1998)

    Article  Google Scholar 

  19. Hassani, B., Hinton, E.: A review of homogenization and topology optimization III-topology optimization using optimality criteria. Computers and Structures 69, 739–756 (1998)

    Article  Google Scholar 

  20. Muñoz-Rojas, P.A., Carniel, T.A., Silva, E.C.N., et al.: Optimization of a unit periodic cell in lattice block materials aimed at thermo-mechanical applications. In: Heat Transfer in Multi-Phase Materials. Springer Berlin, Heidelberg, 301–345 (2011)

    Google Scholar 

  21. Deshpande, V.S., Fleck, N.A., Ashby, M.F.: Effective properties of the octet-truss lattice material. Journal of the Mechanics and Physics of Solids 49, 1747–1769 (2001)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. of Engineering Mechanics, Dalian University of Technology, 116023, Dalian, China

    Geng-Dong Cheng, Yuan-Wu Cai & Liang Xu

Authors
  1. Geng-Dong Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuan-Wu Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liang Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Geng-Dong Cheng.

Additional information

The project was supported by the National Natural Science Foundation of China (91216201).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Cheng, GD., Cai, YW. & Xu, L. Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech Sin 29, 550–556 (2013). https://doi.org/10.1007/s10409-013-0043-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-013-0043-0

Keywords

Search

Navigation