Fixing the direction of droplets in a bifurcating microfluidic junction

Abstract

We present a novel type of microfluidic bifurcating junctions which fixes the droplet’s route. Unlike in regular junctions, where a droplet chooses one of two outputs depending on the (often instantaneous) flow distribution, our modifications direct droplets only to one preferred outlet. As we show, this solution works properly regardless of the variations of flow distribution in a wide range of its amplitude. Such modified junctions allow for the encoding of the droplet’s traffic in the geometry of the device. We compare in a series of experiments different junctions having channels of uniform square cross section. Our observations revealed that a small, local modification of the junction in the form of an additional shallow slit imposes a significant consequence for the flow of droplets at an entire microfluidic network’s scale. Another interesting and helpful feature of these new junctions is that they keep the integrity of long droplets, unlike regular junctions, which tend to split long droplets. Our experimental investigations revealed a complex transformation of the long droplet during its transfer through the modified junction. We show that this transformation resembles the Baker’s transform and can be used for the enhancement of mixing inside the droplets. Finally, we show two examples of microfluidic devices where the deterministic character of these modified junctions is utilized to obtain new, non-trivial functionalities. This approach can be used for the engineering of microfluidic devices with embedded procedures replacing active elements like valves or magnetic/electric fields.

1 Introduction

Microfluidic networks create very unique environments for droplets. The peculiar character of this micro-world has sparked the curiosity of many researchers, which efforts within the last decades opened the way for the development of various strategies for droplet manipulation such as generation (van Steijn et al. 2013), sorting (Tan et al. 2007), trapping (Huebner et al. 2009), splitting (Park et al. 2018) or merging (Bremond et al. 2008). Moreover, droplets can be considered as tiny biochemical reactors (Debski et al. 2018). This opens the way for performing a large number of experiments with slight sample usage.

The specific character of the microfluidic environment consists in the fact that the diameter of microfluidic channels is less than the capillary length. This means that the surface force is the dominant one. Droplets larger than the diameter of the channel are squeezed by the walls and elongated along the channel axis, forming a plug-like shape. Such droplets can be moved by the means of an externally controlled flow of the continuous phase (CP) only in one dimension—along the channel’s axis. Thus, the controlling a droplet may resemble operating an electric railway toy. This way of droplet motion prohibits the spontaneous rearrangement of droplets in their sequence. Therefore, the identity of every single droplet can be easily decoded from its position. Additionally, the CP separates droplets from each other and prevents the cross-contamination of droplets.

More complex operations on the population of droplets such as rearrangement of droplets or redistribution of them between multiple branches of microfluidic networks can be done in junctions connecting at least three channels. Hence, junctions are often a crucial part of the microfluidic networks and, as we will show, the geometry of the junctions can be of critical importance for the flow of the droplets.

As previously shown, the droplets crossing a bifurcating microfluidic junctions can exhibit complex behaviour. Usually, a droplet at a junction either splits into two smaller droplets (Link et al. 2004; Ménétrier-Deremble and Tabeling 2006; Salkin et al. 2013; Hoang et al. 2013; Chen and Deng 2017; Wang et al. 2018, 2019) (for long droplets) or enters one of the two output microchannels (for short droplets) (Engl et al. 2005; Jousse et al. 2006; Schindler and Ajdari 2008; Labrot et al. 2009; Cybulski and Garstecki 2010; Glawdel et al. 2011). In the latter, the choice of the branch into which the droplet enters is determined by the speed and ratio of the outlet flows. Droplets that previously were distributed between different segments of the nontrivial network alter locally the hydrodynamic resistance. In consequence, that leads to a feedback mechanism, where the direction of a single droplet at the junction depends on the state established by previous droplets (Jousse et al. 2006; Cybulski and Garstecki 2010; Glawdel et al. 2011).

Despite the beauty of periodic or chaotic trafficking of droplets in such systems, in some practical applications, it is preferred to make the flow actively controlled or unambiguously determined. The active control on the flow in a junction can be obtained with the use of externally controlled elements as, e.g.: valves (Abate et al. 2010), magnetic (Zhang et al. 2009) and electric (Baret et al. 2009) fields, surface acoustic waves (Franke et al. 2009), electro-wetting (Fair 2007). An overview of different available techniques has been presented by Pit et al. (2015).

Besides the solutions supported by active components, some interesting constructions of junctions have been developed for the passive navigation of droplets. Cristobal et al. (2006) proposed an additional bypass between the output channels to ensure the equal and regular distribution of droplets between the two outlets. Baig at al. proposed a tertiary-junction sensitive to the hydrodynamic properties of the flow of small droplets (Baig et al. 2016). Abbyad et al. proposed the interesting concept of ‘rails’ and ‘anchors’ for guiding droplets motion along fine patterns in channels of the width larger than the droplet’s width (Abbyad et al. 2011).

Passive elements are of importance for the construction of microfluidic droplet systems, where all processes would be determined at the design stage. In this vision, the encoding of protocols or algorithms would be possible due to the integration of multiple microfluidics modules with different functionalities. However, the set of available passive elements is still not sufficient and it lacks components performing some critical operations. One of them is a guiding junction, which (1) fixes the direction of fully confined long droplets, and (2) keep droplets undivided.

In this work, we propose a simple and robust modification of a junction by the use of a bypass slit. This element is a shallow groove less than half the height of the channel. As we showed in previous publications (van Steijn et al. 2013; Korczyk et al. 2013; Zaremba et al. 2018), the bypass slit can be used for altering the difference between the speed of the droplet and the speed of the CP. Due to the change of dimensions between the main channel and the bypass, the droplet does not penetrate the slit. The penetration would require the formation of a high curvature and an increase of the surface’s potential energy, which the droplet tends to minimize. Thus, the bypasses are available exclusively for the flow of the CP.

Intuitively we can expect that the modification of the junction by the addition of a bypass can break the local symmetry of the flow and in consequence can direct a droplet to a preferred output. We show that a junction with an added bypass is a very robust solution working correctly in a wide range of flow parameters. Interestingly, we observed that the kinetic analysis of the droplet’s deformation at the junction reveals the complex morphological transformation of its interior. The proposed solution allows for the manipulation on long droplets where the length is several times longer than the width of the channels.

Finally, we present some simple examples of the use of the modified junctions.

2 Materials and methods

Fig. 1

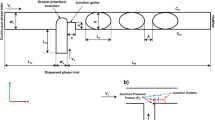
Scheme of the microfluidic loop-device for the analysis of different constructions of junctions: a the general scheme of the device: A—inlet of the continuous phase: B—inlet of the droplet phase, C—junction for the generation of droplets, D—the section with the loop, E—the output; b details of the loop consisting of two identical junctions bifurcating the input flow into two branches of the same length. The loop was constructed to obey the rotational symmetry of $180^{\circ }$; different junctions constructions used in this research: c the regular, symmetric junction (type J0); d the junction with an additional slit in the right output (type J1); e the junction with additional slits in the output channel and in the input channel (type J2); f the junction with additional slits in the output and two slits on both sides of the input channel (type J3)

2.1 Microfluidic devices fabrication

The microfluidic devices were milled from a transparent polycarbonate plate using a CNC milling-engraving machine. A 2-flute fishtail milling bit of diameter around $400 \ \upmu {\text {m}}$ was used to engrave the channels and the slit-bypasses. Microfluidic structures were enclosed by bonding them with another polycarbonate plate from above at high temperature and pressure. The second plate contained the holes that were used for inlets and outlets.

A more detailed description can be found in our previous article where microfluidic devices were fabricated in a similar matter (Zaremba et al. 2018).

2.2 Fluid-specific details

For the CP, we used n-hexadecane 95% (Alfa Aesar, Germany). For the droplet phase, we used distilled water coloured with methylene blue. The surfactant (Span-80, Fluke Analytical, Germany) was added to the n-hexadecane with concentration of about 0.5% to avoid the wetting of the channel walls by the droplets.

The n-hexadecane density is $0.773 \ {\text {g/ml}}$ and its dynamic viscosity is $3.0041 \ {\text {mPa s}}$ at $25 \ ^{\circ } {\text {C}}$. The surface tension between the DP and the CP is 5.34 mN/m (after about 45 s since the creation of the droplet) measured with the pendant drop method using DataPhysics OCA15EC instrument and OpenDrop open-source software (Berry et al. 2015). These values were used later in the article to calculate the capillary number.

2.3 Experimental setup and measurements

Experiments consisted only of visual observations of flows in fabricated transparent microfluidic devices. All devices had the same design shown in Fig. 1a and network structure shown in Fig. 1b. Each device had their own type of junction. The used junctions are shown in Fig. 1c–f. The flows investigated in the microfluidic device were visualized using a Huvitz HSZ-645TR stereoscope equipped with a 0.5x objective and an IDS UI-3274-LE-C-HQ digital camera. Recorded images were stored on a PC for further analysis. Software written in Python and using OpenCV and Trackpy were used for the detection of droplets on sequences of images for speed and position estimation.

The velocity field of the CP flow in the bypass was estimated using particle image velocimetry technique (PIV). For this analysis, the pco.1200hs high-speed digital camera (PCO Imaging) and Nikon Eclipse E-50i microscope equipped with a 10 $\times$/0.3 objective (Nikon LU Plan Fluor) were used. The analysed flow was seeded by glass spheres (tracer particles) with a diameter of $12 \ \upmu {\text {m}}$ and a density similar to the liquids, to minimise buoyancy effects. The suspension was obtained by leaving a highly concentrated solution of particles for a few days in a tall cylinder. Afterwards, a syringe was used to extract the solution from the center of this cylinder. In this way, a fairly low concentration of particles in the liquid was obtained. To increase the number of particles in the image, experiments with the same droplet and parameters were repeated many times. Next, sequences were synchronized and merged in one sequence by the minimization of pixel intensity using ImageJ. Only the bypass was analysed using PIV. The binary mask for the analysed part of the velocity field was created based on the detected edges of the image with the use of a raster graphics editor. The recording framerate was set to 100 fps with $100 \ \upmu {\text {s}}$ exposure time. To improve the detection of particles in PIV, the background was removed and a median filter and thresholding of images was used. The background was obtained by the maximization of pixel intensity in a sequence of images. The open-source software OpenPIV-C++ (Taylor et al. 2010) was used to calculate the velocity field of the bypass. A window with 64 pixel of horizontal and vertical size and 50% overlap was used for the correlation algorithm.

Liquids were pumped by precise and pulsation-free syringe pumps (neMESYS, Cetoni GmbH) equipped with 1.0 ml syringes made of borosilicate glass with a PTFE plunger (ILS Innovative Labor Systeme GmbH). Syringes were connected with the microfluidic device using polyethylene tubing with inner and outer diameter equal to 0.76 mm and 1.22 mm, respectively (Intramedic$^{\circledR }$, Becton Dickinson Co.). The flow rates used in our work are in the 0.4–3.6 ml/h (Ca = $4.243 \times 10^{-4}$ − $38.263 \times 10^{-4}$) range. Droplets were created with the use of a T-junction geometry (area C in Fig. 1a).

2.4 Numerical approach

For the numerical analysis, we used the volume-of-fluid (VOF) model to simulate the flow of the droplets. Additionally, we used the species transport model to show the Baker’s transform. All the computations were done with the use of ANSYS Fluent software based upon the finite volume method. The basic equations to simulate the flow are the incompressible Navier–Stokes equations:

$$\begin{aligned}&\nabla \cdot \mathbf{u } =0, \end{aligned}$$

(1)

$$\begin{aligned}\frac{\partial \rho \mathbf{u }}{\partial t} + \nabla \cdot (\rho \mathbf{uu } ) &= -\nabla p + \nabla \cdot [\mu (\nabla \mathbf{u } + \nabla \mathbf{u }^\mathbf T )] \nonumber \\&\quad + \gamma \frac{p \kappa \mathbf{n }}{\frac{1}{2} ( \rho _1 + \rho _2 )}, \end{aligned}$$

(2)

where $\rho$—density, $\mathbf{u }$—fluid velocity vector, t—time and p—pressure. The last term in the momentum equation refers to the surface tension, wherein $\gamma$ is the surface tension coefficient and $\kappa$ is the curvature and $\mathbf{n }$ the surface normal vector. The subscripts in the denominator dictate from which phase’s density is used. Additionally, for multiphase flow, a volume fraction function $\alpha$ is added to the set of equations, that takes the value of 0 for one of the phases, and the value of 1 for the other.

$$\begin{aligned} \frac{\partial \alpha }{\partial t} + \nabla \cdot \left( \mathbf{u } \alpha \right) = 0. \end{aligned}$$

(3)

After obtaining $\alpha$ in the domain, we can compute the density and the viscosity:

$$\begin{aligned} \rho= & {} \alpha \rho _1 + \left( 1-\alpha \right) \rho _2, \end{aligned}$$

(4)

$$\begin{aligned} \mu= & {} \alpha \mu _1 + \left( 1-\alpha \right) \mu _2. \end{aligned}$$

(5)

The species transport model is governed by the following equation:

$$\begin{aligned} \frac{\partial \rho Y_{i}}{\partial t} + \nabla \cdot (\rho \mathbf{u } Y_{i} ) = \nabla \cdot (\rho D_{i} \nabla Y_{i}), \end{aligned}$$

(6)

where $Y_{i}$ is the local mass fraction for each species and $D_{i}$ is the mass diffusion coefficient. To show the Baker’s transform, we limited the mass diffusion by applying a value of order $10^{-15}$ to its coefficient. We used a variable time stepping method that allowed the simulation to choose a time step between $10^{-7}$ and $10^{-4}$ s based on the global Courant’s number. A computational orthogonal and uniform mesh was generated upon the constraints of having at least $20 \times 20$ elements in the cross section of the channel.

3 Results and discussion

3.1 Observations of the effect of modification J1 on the flow of short droplets

Fig. 2

Observations of droplets in loop devices. Comparison of junctions type J0 and type J1. the snapshots taken after introducing 64 droplets for junctions types J0 (a) and J1 (b), respectively, and the snapshots taken after introducing 150 droplets for junctions types J0 (c) and J1 (d), respectively

Fig. 3

Quantitative analysis of the effect of junction geometry on the distribution of droplets—comparison of junction types J0 and J1. Measurements of the normalized number of droplets in the left branch of the loop $n_{\text {L}}$ and normalized speed of droplets in the left branch $v_{\text {L}}$ of the loop as functions of the droplet’s number i. Experiments were carried out at a constant CP flow equal to 3 ml/h and DP equal to 0.5 ml/h. The length of the droplets was 0.68 mm

The various observations confirmed that in the bifurcating junction a single short droplet is directed into the channel with the higher flow velocity (Parthiban and Khan 2013; Wang and Vanapalli 2014; Cybulski et al. 2015). As the droplet changes the resistance of the flow in a channel, the distribution of flows between the two outputs will depend on the current number of droplets in each of the branches. This feedback mechanism causes droplets in such systems to exhibit periodical or chaotic behaviour (Engl et al. 2005; Jousse et al. 2006; Schindler and Ajdari 2008; Maddala et al. 2014). Too small distances between droplets entering the junction may result in collisions, which affect the direction of droplets (Belloul et al. 2011). In this work, we made sure that the distances between consecutive droplets were sufficient to avoid collisions.

In this paper, we propose such junction modifications, which fix the direction of droplets regardless of the flow’s history. We start by presenting the comparison of a regular junction (type J0—see Fig. 1a) with a simple modified junction (type J1—see Fig. 1b). The only difference between these junctions is an additional slit which disturbs the symmetry of the modified junction in comparison to the regular one.

To investigate the effect of the considered modification, we used two microfluidic loop devices—one with the regular junction type J0, and the other one with the junction J1. Droplets of constant length and with constant frequency were generated in the device at the beginning of the loop and then the chain of droplets entered the loop with a constant speed. The frequency of droplets generation was set low enough to avoid collisions in the junction. Every single droplet getting into the bifurcating junctions can choose between two possible routes: turning left or right. We observed long sequences of short droplets passing through both loops.

Our observations of the regular junction (type J0) confirmed that the symmetry of the device results in the equalization of the distribution of droplets in both arms. The first droplet enters the left branch. The choice of the branch is likely determined by some imperfections during device fabrication resulting in not perfectly equal resistances between both the branches. These imperfections are small in comparison to the increase of resistance introduced by a single droplet so the next droplet enters the opposite branch as the empty branch has smaller resistance. Each next droplet so chooses the route to make the distribution of droplets closer to the equilibrium (see Fig. 2a). The number of droplets in both branches increases to a maximum value limited by the length of the branches. After that the number of droplets getting into the loop is balanced by the number of droplets coming out. In that case, the system reaches a stationary state with the number of droplets in the loop fluctuating slightly around a constant value (42 droplets in each of the branches—see Fig. 2c).

The situation in the case of the loop with the modified junction type J1 is very different. As shown in Fig. 2b, the first 63 droplets flow only into the left branch. The 64-th droplet is the first one, which turns right. Notice that in the regular junction’s case, droplets tend to distribute equally. The intriguing conclusion is that the local asymmetry of the junction—small in comparison to the size of the whole loop—results in a significant asymmetry of droplet flow in the whole device.

More information can be obtained from the quantitative analysis of the processes observed in both devices. Starting from the first droplet entering the loop, each consecutive i-th droplet changes the state of the device. The state established after introducing into the loop the i-th droplet can be characterized by the numbers of droplets $N_{\text {L}}(i)$, $N_{\text {R}}(i)$ and the mean velocities of flows $V_{\text {L}}(i)$, $V_{\text {R}}(i)$ in the left branch (subscript L) and the right one (subscript R), respectively.

Notice that the sum of velocities $V_{\text {L}}(i)+V_{\text {R}}\left( i\right) =V_{\text {IN}}$ is constant as the velocity in the inlet channel $V_{\text {IN}}$ is constant. Hence, we can use only one quantity $v_{\text {L}}\left( i\right) =V_{\text {L}}(i)/V_{\text {IN}}$ for the description of the flow distribution and we can limit only to the measurement of the speed in the left branch. We estimated $V_{\text {L}}(i)$ assuming that (with the precision sufficient for this simple analysis) it is equal to the measured speed of the droplets in the left branch. $V_{\text {IN}}$ was estimated in a similar way by averaging speed measurements of droplets in the input channel. The image analysis of frame sequences was used for the measurements of velocities.

Thus, the quantification of the distribution of flows ($v_{\text {L}}\left( i\right)$) can be obtained even in the absence of droplets in the right branch (e.g. for $i<64$ in the modified junction).

The distribution of droplets between both branches was expressed by the number of droplets in the left branch normalized by the sum of droplets in both branches $n_{\text {L}}(i)=\frac{N_{\text {L}}(i)}{N_{\text {L}}(i)+N_{\text {R}}(i)}$.

The results of the analysis for both junctions are plotted in Fig. 3. Analysing the plots from the beginning of the process one intriguing and not obvious fact can be directly discovered. Here, we assume that the single first droplet does not significantly affect the flow. Thus, the value of $v_{\text {L}} \ \left( i=1\right)$ provides the information about the distribution of the CP flow in the loop device without droplets (for $i=0$). The fact that the measured values of $v_{\text {L}} \ \left( i=1\right)$ for both types of junctions are almost identical (close to 0.5) reveals that the modification of the junction does not affect the one-phase flow. Before the droplets enter the junctions, the flow of the CP is distributed equally between both branches of the loop due to their equal resistances and regardless of the different geometries of the junctions. These observations indicate the significant difference between one-phase flow and two-phase flow. In the presence of droplets, we observed a substantial flow asymmetry in the modified junction.

Let us analyse the further evolution of the states for both types of junctions exploring the variability with droplet’s number i of both $v_{\text {L}}(i)$ and $n_{\text {L}}(i)$ plotted in Fig. 3.

In the case of the regular junction (type J0), the value of $v_{\text {L}}$ is close to 0.5 starting from the first droplet and then fluctuates slightly around it. The value of $n_{\text {L}}(i)$ starts from 1 (the first droplet accidentally chooses the left branch) and quickly converges to the value close to 0.5. This indicates that in the case of the regular, symmetric junction the system tends to restore symmetric state ($n_{\text {L}}=0.5$, $v_{\text {L}}=0.5$), reflecting the symmetry of the loop-device.

In the case of the modified junction (type J1), the value of $v_{\text {L}}$ starts from 0.5 and then it decreases with each successive droplet as is shown in the plot. For $i<64$, droplets enter only into the left branch. Hence, for the first pack of 63 droplets $n_{\text {L}}={\text {const}}=1$. Droplets form a long chain in the left branch with decreasing spaces between consecutive droplets, corresponding to the fall of $v_{\text {L}}$. For $i>63$, $v_{\text {L}}$ approaches the value $v_{\text {Lcrit}}=0.26$, where $v_{\text {Lcrit}}$ is estimated as an average of $v_{\text {L}}$ for $i>63$. From this point, some droplets are guided into the right channel, while the majority of them is still guided to the left branch. This is reflected in the decreasing number $n_{\text {L}}$.

Hence, the proper guiding of the droplets into the left channel is possible for the limited ratio of velocities in both output channels. In this case, droplets are directed into the left channel for $v_{\text {L}}>v_{\text {Lcrit}}$ which is equivalent to the critical ratio $V_{\text {L}}/V_{\text {R}}<0.35$.

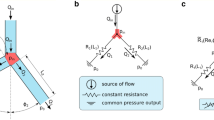
The decay of $v_{\text {L}}(i)$ in the modified junction (type J1) can be explained by a simple model. Let us assume that both arms of the loop are characterized by the same value of resistance R. The presence of a single droplet in the channel increases the entire resistance. Let us assume that each next droplet increases the entire resistance of the channel by a constant amount of $R_{\text {D}}$. Equating instantaneous pressure drops in both branches of the loop, we obtain the equation taking into account the effect of the distribution of droplets:

$$\begin{aligned} Q_{\text {R}} \cdot \left( R+N_{\text {R}}R_{\text {D}}\right) =Q_{\text {L}} \cdot (R+N_{\text {L}}R_{\text {D}}), \end{aligned}$$

(7)

where $Q_{\text {R}}=V_{\text {R}}A_{\text {ch}}$, $Q_{\text {L}}=V_{\text {L}}A_{\text {ch}}$ are rates of flows in both branches, respectively, with $A_{\text {ch}}$ being the area of the cross section of the channel, the same for both branches.

For $i<64$, there are no droplets in the right branch of the modified junction so $N_{\text {R}}=0$ and $N_{\text {L}}=i$. The above equation in these conditions yields the equation for the evolution of $v_{\text {L}}\left( i\right)$ in the beginning period ($i<64$), when all droplets go into the left branch and $v_{\text {L}}>v_{\text {Lcrit}}$

$$\begin{aligned} v_{\text {L}}\left( i\right) =\frac{1}{2+i{\cdot }r_{\text {D}}}, \end{aligned}$$

(8)

where the coefficient $r_{\text {D}}=R_{\text {D}}/R$ can be found due to the relation:

$$\begin{aligned} r_{\text {D}}=\frac{1-2v_{\text {L}}(i)}{\left( N_{\text {R}}\left( i\right) +N_{\text {L}}\left( i\right) \right) {\cdot }v_{\text {L}}\left( i\right) -N_{\text {R}}\left( i\right) }. \end{aligned}$$

(9)

This coefficient can be estimated from the values of $v_{\text {L}}$, $N_{\text {R}}$, $N_{\text {L}}$ averaged after the system reaches the quasi-steady state (for $i>150$). In the case of our device, $r_{\text {D}}=0.038$.

In general, the route of the i-th droplet is determined by the distribution of flows in the junction established due to the flow of previous droplets. Hence, if $v_{\text {L}}\left( i-1\right)>v_{\text {Lcrit}}$ the i-th droplet goes into the left branch, or contrarily into the right branch if $v_{\text {L}}\left( i-1\right) <v_{\text {Lcrit}}$. This general rule is valid for any junction geometry characterized by the specific value of $v_{\text {Lcrit}}$. While the broken symmetry in the modified junction (type J1) establishes $v_{\text {Lcrit}}=0.26$, in the regular junction (type J0), the symmetry of the setup results in $v_{\text {Lcrit}}=0.5$.

This explains the fluctuations of $v_{\text {L}}$ and $n_{\text {L}}$ in the terminal stage after the system reaches the quasi-steady state. Each droplet entering into or getting out of the loop changes the state of the system; hence, the resultant $v_{\text {L}}$ is slightly above or below the value of $v_{\text {Lcrit}}$.

The above analysis shows that the proposed loop device can be used for a comprehensive analysis of the impact of junction modifications on the motion of droplets. Such crucial parameters like $v_{\text {Lcrit}}$ and $r_{\text {D}}$ can be estimated with the use of a simple experimental setup and with relatively small effort.

3.2 Observations of long droplets in the modified junction type J1

In the previous examples, we analysed the motion of short confined droplets of comparable length to the width of the channel W. We can expect that the modification of the junction may affect the motion of long droplets (with the length significantly larger than W). As we will show, the proposed modification of the junction significantly extends the possibilities of this simple bifurcation.

Unlike short droplets, long droplets generally break into two parts in regular junctions (Chen and Deng 2017; Sun et al. 2018). We observed that phenomenon in our loop-device with the regular junction J0, but in the case of the modified junctions, a long droplet can go through the junction without splitting.

Fig. 4

Images from experiments with long droplets in a microfluidic loop device with a modified junction of type J1. The length of the produced droplets was constant and equal to 5.5 times the width of the channel. Images show the quasi-steady state for two different values of input flow velocity: a $Q_{\text {IN}}= 1.1 \ {\text {ml/h}}$, $V_{\text {IN}}=1.7 \ {\text {mm/s}}$. All droplets enter the left branch. b $Q_{\text {IN}}= 1.7 \ {\text {ml/h}}$, $V_{\text {IN}}= 2.7 \ {\text {mm/s}}$. Droplets partially break in the junction

For the demonstration, we present in Fig. 4 two observations of long droplets series travelling through the loop device with a junction type J1. These two experimental runs were performed for two different values of inlet velocity $V_{\text {IN}}$. They show that for $V_{\text {IN}}=1.7 \ {\text {mm/s}}$ the long droplet (1) keeps its integrity and (2) enters the left branch of the loop-device (see Fig. 4a). While for $V_{\text {IN}}=2.7 \ {\text {mm/s}}$, the droplet is split into uneven parts between both branches (see Fig. 4b).

Fig. 5

The long droplet in the modified junction type J1. The sequence of consecutive snapshots for: left column—non-break-up mode for $V_{\text {IN}}=1.9 \ {\text {mm/s}}$, and right column—break-up mode for $V_{\text {IN}}=2.7 \ {\text {mm/s}}$

The sequence of consecutive snapshots of the long droplet during its movement through the junction reveals the non-trivial transformation of the droplet (see Fig. 5). The droplet produces a temporary ‘protrusion’ in the right output. Then, depending on the value of $V_{\text {IN}}$, this ‘protrusion’ can be either pulled by the main part of the droplet into the left output (for small $V_{\text {IN}}$) or can detach from the main part of the droplet and go into the right output (for large $V_{\text {IN}}$).

Thus, we can expect that in general, the behaviour of the droplet in the junction should depend on the set of parameters such as the length of a droplet, the geometry of the modification, capillary number and flow distribution.

3.3 Kinetic analysis of long droplets in the modified junction of type J1

Fig. 6

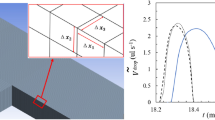
Kinetics of a long droplet flowing through the junction with a single slit-bypass. a The sequence of snapshots of a droplet for four stages labelled by roman numbers from I to IV. The transient periods are labelled by Roman numbers and arrows. The characteristic flow structures (reconstructed on the basis of experiments) are schematically shown as lines with arrows. b Direct visualizations of tracer particles trajectories in the bypass. Each image obtained by the imposition of 50 consecutive frames registered at the speed of 100 fps. Thus, the length of the smudges is proportional to the velocity of the tracer particles

Fig. 7

Kinetics of a long droplet flowing through the junction with a single slit-bypass. Left axis—the time evolution of the length of the ‘head’ $L_{\text {H}}$, the length of the ‘tail’ $L_{\text {T}}$ and the length of the ‘protrusion’ $L_{\text {P}}$ normalized by the width of the channel W. Right axis—the intensity of the flow through the bypass $p_{\text {B}}$. In the inset—the scheme illustrating the decomposition of the deformed droplet into ‘head’—the purple arm, ‘protrusion’—the green arm, the ‘tail’—the orange arm of the droplet. The additional part of the droplet connecting all arms is presented as a circle in the centre of the junction. The additional auxiliary thin black lines show the linearity of parts of the droplet’s flow occurring at a certain time. (Color figure online)

Herein, we present the experimental analysis of the motion of a long droplet travelling through the junction with a single bypass (type J1) without breaking. In the example, we consider an equal flow distribution between both outputs ($V_{\text {L}}=V_{\text {R}}$). Unlike in the previous observations, here only one single long droplet of the length ${L_{\text {D}} = 5.5 W}$ was created and moved at a constant speed ($V_{\text {IN}}= 1.6 \ {\text {mm/s}}$) toward the junction. We observed the process with the use of a microscope and a 100 FPS camera.

These observations allowed us to distinguish between four critical stages of the process as presented in Fig. 6. Besides the observations of the morphological transformation of the droplet, we analysed as well the evolution of the flow through the bypass. The characteristic flow structures were made visible thanks to traces of tiny particles suspended in the CP. The obtained visualizations of streamlines provided insight into the evolution of the morphology and the intensity of the velocity field in the bypass (see Fig. 6b). The flow patterns retrieved from these observations are schematically drafted in the snapshots presenting the droplet at different time points. This shows the interplay between the droplet and the CP flow and reveals the mechanism, which allows the long droplet to keep its integrity. The consecutive stages of the process are labelled in Figs. 6 and 7 by the roman numbers from I to IV. In the following, we will describe the quantitative analysis and then we provide the comprehensive description of these stages.

As we mentioned before, the droplet temporary deforms, expanding into all three channels of the junction (see Fig. 6a, stages from I to III). Hence, in this configuration, the droplet consists of three ‘arms’ connected in the central part of the junction namely: (1) the ‘protrusion’ in the right-output-channel, (2) the so-called ‘tail’—the rear part remaining in the inlet channel and (3) the ‘head’—the front of the droplet expanding into the left channel (see the scheme in the inset in Fig. 7 ).

For a quantitative characterization of the transformation of the droplet’s shape, we measured the instantaneous lengths of each of these ‘arms’, respectively: $L_{\text {P}}$, $L_{\text {T}}$, $L_{\text {H}}$ (see inset in Fig. 7). The droplet of the initial length $L_{\text {D}}$ during the deformation in the junction does not change its volume and, hence, the sum of the length of all arms is constant:

$$\begin{aligned} L_{\text {H}}+L_{\text {P}}+L_{\text {T}}=L_{\text {D}}-L_{\text {J}}, \end{aligned}$$

(10)

where the constant $L_{\text {J}}={\text {const}}={1.3} W$ corresponds to the volume of the droplet in the central part of the junction (see the circle in the graph). The slopes of the length evolution of the arms correspond to the rates of growth of the droplet’s arms ${\text {d}}L_{\text {H}}/{\text {d}}t$, ${\text {d}}L_{\text {P}}/{\text {d}}t$, ${\text {d}}L_{\text {T}}/{\text {d}}t$. As the ‘head’ is pulled into the left branch it expands with the constant rate ${\text {d}}L_{\text {H}}/{\text {d}}t=V_{\text {L}}$. The constant volume of the droplet imposes the speed constraint of the change of $L_{\text {P}}$ and $L_{\text {T}}$. Indeed, time derivation of Eq. (10) yields:

$$\begin{aligned} V_{\text {L}}+\frac{{\text {d}}}{{\text {d}}t}L_{\text {P}}+\frac{{\text {d}}}{{\text {d}}t}L_{\text {T}}=0. \end{aligned}$$

(11)

The quantification of the CP flow intensity through the bypass was performed due to the analysis of additional data—instantaneous 2D velocity fields obtained by the means of PIV. We estimated the transient intensity of the bypass flow $P_{\text {B}}$ by spatial averaging each velocity field over the whole area of the bypass. The dimensionless equivalent $p_{\text {B}}$ was obtained through the normalization of the averaged value of $P_{\text {B}}$ measured before stage I. This quantity reflects very well the variability of the bypass flow; however, the reader should notice that it is not perfectly equal to the flow rate because of some limitations of the 2D PIV technique. Despite these imperfections, the measurements of the intensity $p_{\text {B}}$ provide important information on the activation and deactivation of the bypass flow by a moving droplet.

Now, we will provide a comprehensive description of all critical stages and intervals between them.

Before the droplet enters the junction (prior to stage I), it travels with a constant speed which is reflected in the constant slope of the plot of $L_{\text {T}}/W$ (the position of the rear of the droplet) in Fig. 7. The magnitude of the flow through the bypass is close to its minimum ($p_{\text {B}}\approx 1$).

In stage I, the droplet’s front reaches the junction hence $L_{\text {P}}=0$ and $L_{\text {H}}=0$ (see Fig. 6a and snapshot labeled as I). Then, in the interval between stage I and stage II (denoted as I $\rightarrow {}$ II), the droplet builds up the ‘head’ and the ‘protrusion’, which is reflected in the increase of $L_{\text {H}}$ and $L_{\text {P}}$ in Fig. 7.

The crucial part in this interval is the position of the ‘tail’, which completely blocks the access to the bypass slit from the CP flow from the main channel. We can observe the characteristic circulation zone in the ‘shade’ of the droplet (Fig. 6b). It is related to Lid-driven cavity flow and was observed also in our previous publication (Zaremba et al. 2018). Thus, the activity of the bypass flow measured by $p_{\text {B}}$ is even slightly lower than before stage I.

In consequence, the bypass is effectively switched off and does not affect the droplet. In this situation, the rate of growth of the arms is equal to the flow speed in the branches, so: ${\text {d}}L^{{\text {I}}\rightarrow {{\text {II}}}}_{\text {H}}/{\text {d}}t=V_{\text {L}}$, ${\text {d}}L^{{\text {I}}\rightarrow {{\text {II}}}}_{\text {P}}/{\text {d}}t=V_{\text {R}}$. According to Eq. (11), the expansion of the ‘head’ and the ‘protrusion’ must be compensated by the shrinkage of the ‘tail’ so: ${\text {d}}L_{\text {T}}/{\text {d}}t=-V_{\mathrm{IN}}$. During the interval ${\text {I}}\rightarrow {\text {II}}$, the length ratio of the different arms is equal to the ratio of velocities in both branches: $\frac{L^{\mathrm{I}\rightarrow {\mathrm{II}}}_{\text {H}}}{L^{\mathrm{I}\rightarrow {\mathrm{II}}}_{\text {P}}}=\frac{V_{\text {L}}}{V_{\text {R}}}$.

In stage II, the shrinking length of the ‘tail’ reaches the value, below which it cannot effectively block the CP flow into the bypass: $L^{\mathrm{II}}_{\text {T}}=(\varLambda _{\text {T}}/W+0.5)W$, where $\varLambda _{\text {T}}$ is the width of the entrance to the bypass slit from the main channel (see the inset in Fig. 7). The additional term $0.5\cdot W$ includes the length of the round cap of the droplet. From that point, in the interval ${\mathrm{II}}\rightarrow {\mathrm{III}}$ the ‘tail’ opens the entrance to the bypass up until it completely vanishes in stage III. This process gradually raises the bypass flow. The circulation zone observed previously is replaced by the regular flow of the CP bypassing the ‘protrusion’ in the right output (see Fig. 6b). Due to the activation of the bypass, both the growth of the ‘protrusion’ and the shrinkage of the tail slow down (see the slope of $L_{\text {P}}(t)/W$ and $L_{\text {T}}(t)/W$).

Stage III marks the point when the ‘tail’ completely disappears ($L^{\mathrm{III}}_{\text {T}}=0$) and the ‘protrusion’ reaches its maximum length. What is important, the ‘protrusion’ immediately transforms from the temporary front of the droplet to its end and reverses its direction from expanding to receding. During the interval ${\mathrm{III}}\rightarrow {\mathrm{IV}}$, the entrance of the bypass is completely open for the flow of the CP, while the ‘protrusion’ still occupies the right channel of the junction. In this configuration, the whole flow of the CP must bypass the protrusion through the slit. In result, the bypass flow is at its highest level, what is visible in the visualization of the flow (Fig. 6b) and indicated by the high value of $p_{\text {B}}$ (Fig. 7).

As the ‘head’ of the droplet moves with the constant speed ${\text {d}}L_{\text {H}}/{\text {d}}t=V_{\text {L}}$, it pulls the protrusion into the left output. Due to the absence of the tail, the integrity of the droplet requires that both its front and back move with the same velocity, so ${\text {d}}L_{\text {P}}/{\text {d}}t=-{\text {d}}L_{\text {H}}/{\text {d}}t$. The unique and intriguing character of this process consists of the fact that the protrusion moves opposite to the CP flow. The protrusion in the interval ${\mathrm{III}}\rightarrow {\mathrm{IV}}$ shrinks after the expansion in the previous interval. This fact is reflected by the change of the slope of $L_{\text {P}}(t)$ in the plot in Fig. 7. In this way, the ‘protrusion’ is gradually engulfed by the ‘head’.

Finally, the last stage IV marks the complete disappearance of the ‘protrusion’ ($L^{\mathrm{IV}}_{\text {P}}=0$). The whole volume of the droplet has been entirely transferred towards the ‘head’ in the left output. After that, the whole droplet travels in the left branch of the loop-device with the speed $V_{\text {L}}$. The transfer process of the droplet from the input channel to the left branch is completed. The bypass flow changes back to its lowest level as before the entrance of the droplet in the junction.

The above analysis shows in details the transfer process of a long droplet into the left branch of the loop. This explains as well the mechanism responsible for the flow of short droplets. Similarly, as in the case of long droplets, the short ones are pulled into the left branch due to the bypass, which redirects the flow of the CP into the right branch. In this case, the flow of two liquid phases can be locally decoupled and become asymmetric. The droplet flows into the channel without the bypass and the CP flows through the bypass into the opposite channel.

3.4 Effect of the Baker’s transform

As we showed before, the droplet during its movement through the junction is a subject of a non-trivial transformation which includes the generation of a temporary ‘protrusion’ and its later shrinkage. In the previous section, we focused on the analysis of the droplet’s shape. Now, we discuss the rearrangement of the droplet’s internal mass distribution. To visualize the effect of the flow within the droplet, we performed simple observations of Janus droplets, i.e. droplets composed of two different parts.

Fig. 8

Visualizations of the mixing process inside the droplet. a Microscopic image of the generation of Janus droplets in the cross-flow device. b Mixing inside the Janus droplet travelling through a straight channel: the left image—droplet just after its generation; the right image—droplet after travelling the distance of ten droplet’s lengths. c The Janus droplet flowing through the modified junction—the composition of three images of the same droplet in the consecutive positions from T1 to T3. In the inset—the schematic pictogram of the transformation of the droplet. d The schematic view of the separation plane in position T1 and after the transformation in position T2

We generated Janus droplets in a cross junction (Fig. 8a) where two opposite streams of 80% glycerol-in-water solution meet. One of the streams is distinguished by the addition of ink. Due to that, the merged streams form a well-visible two-layered parallel flow in the main channel. The additional cross-flow of the continuous immiscible phase (oil) results in the generation of droplets consisting of two symmetrical halves of different colours. To explain the peculiar character of the droplet’s transformation in the modified junction, we firstly present the observations of Janus droplets travelling through a straight channel. It is a well-known fact that the symmetry of the internal flow within the droplet inhibits the exchange of mass across the symmetry plane (Tice et al. 2003). Hence, despite the continuous re-circulating flow inside the droplet, the homogenization of the content of the symmetrical Janus droplet is only thanks to the diffusion across the separation plane.

Figure 8b presents two images of the same droplet, the left one—the droplet just after its generation, the right one—the droplet after travelling the distance of ten droplet’s lengths. We can see that the droplet in its initial state is not perfectly symmetrical (with the small dose of ink in the bottom half). Despite that, we observe that the initial stratification is conserved after the droplet moves over the distance of ten its lengths. The ink’s concentration is homogenized only within the separated halves. This is the reason why the initially introduced portion of ink in the bottom half, after mixing, results in the fade bright-blue colour of the bottom half. However, the plane of separation in the middle of the droplet is still well visible and sharp.

Figure 8c presents the results of experiments with the Janus droplet flowing through the modified junction. The image shows the composition of three images of the same droplet in three consecutive positions labelled as T1, T2 and T3. In position T1, the droplet is approaching the junction and we can see the sharp stratification of the ink’s concentration in the middle plane of the droplet. The position T2 corresponds to stage III mentioned in the previous section where the ‘tail’ has completely disappeared and the head starts to pull the ‘protrusion’ into the left output. What is important is that the whole volume of the blue half of the droplet has been redirected to the ‘head’ while the bottom, clear half has been redirected to the ‘protrusion’.

In other words, the droplet during the transition from T1 to T2 is being precisely cut in the plane of separation. Simultaneously, both halves are being gradually folded out in opposite directions. This process is schematically shown in the inset in Fig. 8c. This transformation resembles one iteration of the Baker’s transform applied to the long droplet. In result, the significant rearrangement of the droplet’s interior is obtained. Notice that the upper half of the droplet is transferred to its front part, the bottom half to its rear part and the previous rear part is transferred to the central part of the droplet.

Crucial for the homogenization of the droplet’s content is the reorientation of the plane of separation of the two aqueous phases (see Fig. 8d). In position T1, the plane of separation is in the plane of symmetry of the droplet and is parallel to the streamlines of the internal flow. In position T2, this plane is reoriented and becomes perpendicular to the streamlines. Afterwards, the plane of separation is carried by the flow and gradually stretched and deformed. This leads to the homogenization of the droplet’s content.

Fig. 9

The mixing process of the reoriented Janus droplet. The contrast of the concentration c as a function of the normalized distance travelled by the droplet $d=D/L_{\text {D}}$. The snapshots from the simulations show the evolution of the instantaneous distribution of the indicator in the middle-plane of the droplet (see the colorbar for reference). (Color figure online)

The efficiency of this process is clearly seen in the image of the droplet after travelling the distance of about one droplet’s length (position T3 in Fig. 8c). Although the droplet is not yet completely homogenized, the blue dye is distributed over the whole droplet without any visible sharp separation of areas with different concentrations of ink, unlike in the case of the straight channel, where the sharp separation between two domains is conserved over a much longer distance. To quantitatively estimate the mixing rate after the reorientation of the separation plane, we conducted numerical simulations (see Fig. 9). The starting point of these simulations was a droplet composed of two parts with different concentrations of the passive indicator with the separation plane perpendicular to the axis of the channel. Initially, the droplet was divided into two halves: (1) the front part with the initial concentration $C_{\text {F}}{(t=0)}=C_0$ and (2) the rear part $C_{\text {R}}{(t=0)}=0$ We set a very low diffusion coefficient ($2.88 \times 10^{-15} {\text {m}}^2/{\text {s}}$ what corresponds to the value for water, decreased $10^6$ times), so the flow inside the droplet was the only mechanism which would mix the interior of the droplet. During the simulation, the droplet was travelling through a channel of square cross section with a constant speed hence the distance D travelled by the droplet was proportional to time. For each simulation step, we estimated the normalized contrast between the two parts of the droplet defined as $c(d)=(C_{\text {F}}(d)-C_{\text {R}}(d))/C_0$, where $C_{\text {F}}(d)$ and $C_{\text {R}}(d)$ are instantaneous average concentrations in both parts of the droplet, respectively, and $d=D/L_{\text {D}}$ is the distance travelled by the droplet normalized by the length of the droplet. This coefficient starts from the value $c(d=0)=1$ and decreases with time. The minimal possible value $c=0$ corresponds to the equal distribution of the passive indicator in both parts of the droplet. The data obtained from the numerical simulations show the exponential decay of the contrast with the fitted relation in the form: $c(d)=\exp (-d/2.16)$. This implies that after travelling the distance $D=5L_{\text {D}}$, the contrast c falls to a value of about 0.1.

The modified junction’s geometry realizes the Baker’s transform on the droplet’s interior which radically improves the content’s mixing in long droplets. The rearrangement of the spatial distribution of the droplet’s content can be used to prevent the sedimentation of particles in the rear part of the droplet (Hein et al. 2015).

3.5 Mechanism of droplet break-up

The splitting of the droplet in the junction may have potential applications; however, here we consider how it can be avoided. We want to retain the integrity of the droplet. The mechanism of droplet breakup was the subject of numerous investigations (Link et al. 2004; Ménétrier-Deremble and Tabeling 2006; Salkin et al. 2013; Hoang et al. 2013; Chen and Deng 2017; Wang et al. 2018, 2019); however, until now the effect of an additional bypass was not considered. Here, we present the analysis of the transition between break-up and non-break-up modes of a droplet in the junction with the bypass. The comparison of observations of broken droplets and unbroken ones reveals that the transformation of the shape of the droplet in both cases is very similar until stage ${\mathrm{III}}$, i.e. until the complete disappearance of the ‘tail’. This is the critical point, for the further fate of the droplet (compare snapshots in Fig. 5). In the case of the non-break-up mode, after stage ${\mathrm{III}}$, the ‘protrusion’ is effectively pulled into the left channel.

In the case of the break-up mode, the split of the droplet occurs in the central part of the junction similarly like in the case of the junction without the bypass. Therefore, we can expect that a similar mechanism of deformation of the ‘elbow’, connecting the ‘protrusion’ and the ‘head’, appears in the modified junction. In the break-up scenario, the incoming flow of the CP causes the deflection of the ‘elbow’ and the droplet finally breaks.

The bypass in the modified junction lowers the pressure build-up in the junction so the pressure drop along the ‘protrusion’ $\Delta P_{\text {P}}$ can be estimated as:

$$\begin{aligned} \Delta P_{\text {P}} = \alpha _{\text {B}} \cdot V_{\text {IN}} \cdot A_{\text {ch}} \cdot (L_{\text {P}}^{\mathrm{III}}-L_0) \cdot \mu \cdot A^{-2}_{\text {B}}, \end{aligned}$$

(12)

where $\alpha _{\text {B}}$ is the geometrical non-dimensional factor of the resistance of the bypass, $A_{\text {ch}}$, $A_{\text {B}}$ are the areas of the cross sections of the input channel and the bypass slit, respectively, $\mu$ is the dynamic viscosity of the CP, and $L_0$ is the additional correction factor.

The mechanism that resists the ‘deflection’ of the ‘elbow’ is the Laplace pressure, which can be described as the product of the interfacial tension coefficient and the mean curvature of the ‘elbow’ H:

$$\begin{aligned} \Delta P_{\text {L}}= 2 \gamma H. \end{aligned}$$

(13)

Here, we can assume that the shape of the non-deformed ‘elbow’ is defined single-handedly by the geometry of the device.

Equating $\Delta P_{\text {P}}$ and $\Delta P_{\text {L}}$, we obtain the transition between break-up and no-break-up modes:

$$\begin{aligned} L^{\mathrm{III}}_{\text {P}}/W=\beta /Ca + l_0 , \end{aligned}$$

(14)

where $\beta =2 \cdot A_{\text {ch}} \cdot A^{-2}_{\text {B}} \cdot H \cdot W^{-1}$ and $l_0=L_0/W$ are non-dimensional fitting parameters.

Note that this simplified model does not take into account the velocity of the head and additional shear acting on the protrusion. Despite the assumed simplifications, the model correctly explains the transition from the break-up mode to the no-break-up mode, what we observed experimentally (see Fig. 10). The values of fitted parameters are $\beta = 0.0041$ and $l_0 = 0.24$. These parameters are specific for the investigated geometry of the junction and may vary for other geometries.

Fig. 10

Phase diagram of operational modes of the junction type J1 in the space of parameters $L^{\mathrm{III}}_{\text {P}}/W$ vs Ca

Besides the above-mentioned dynamic constraints for the no-break-up mode, there is an additional geometrical restriction for the maximal length of the ‘protrusion’. Indeed, once the ‘protrusion’ blocks the flow of the CP from the bypass to the right branch, the ‘protrusion’ is pulled into it with the speed $V_{\text {R}}$ and cannot recede, which results in the break-up of the droplet. This geometrical constriction limits the length of the ‘protrusion’ to $L_{\text {P}}=\varLambda _{\text {P}} + 0.5W$ and is plotted in the graph as the horizontal line.

The next question is what does the maximal length of the ‘protrusion’ $L^{\mathrm{III}}$ depend on? As we mentioned before, the ‘protrusion’ develops within the first two intervals $\text {I}\rightarrow {\mathrm{II}}$ and $\text {II}\rightarrow {\mathrm{III}}$. In the first interval, it grows with the maximal rate ${\text {d}}L^{\mathrm{I}\rightarrow {\mathrm{II}}}_{\text {P}}/{\text {d}}t=V_{\text {R}}$. In the interval from $\text {II}\rightarrow {\mathrm{III}}$, the activated bypass flow lowers the rate of growth of the protrusion ${\text {d}}L^{\mathrm{II}\rightarrow {\mathrm{III}}}_{\text {P}}/{\text {d}}t<V_{\text {R}}$. Taking into account that ${\text {d}}L_{\text {H}}/{\text {d}}t=const=V_{\text {L}}$ we can state:

$$\begin{aligned} \frac{L^{\mathrm{III}}_{\text {P}}}{L^{\mathrm{III}}_{\text {H}}}<\frac{V_{\text {R}}}{V_{\text {L}}}. \end{aligned}$$

(15)

For the given length of the droplet $L_{\text {D}}$, the maximal available length of the protrusion can be roughly described by the following form, which includes in addition the geometrical restriction:

$$\begin{aligned} L^{\mathrm{III}}_{\text {P}} \le (L_{\text {D}}-L_{\text {J}})v_{\text {R}}<\varLambda _{\text {P}}+0.5W, \end{aligned}$$

(16)

where $v_{\text {R}}=V_{\text {R}}/V_{\text {IN}}=1-v_{\text {L}}$.

Notice that the geometrical restriction for the maximal length of the protrusion in the non-break-up mode sets the limit for the longest droplet, which can go through the junction without being split:

$$\begin{aligned} L_{\text {D}} \le (\varLambda _{\text {P}}+0.5W) \cdot v_{\text {R}}^{-1} +L_{\text {J}}. \end{aligned}$$

(17)

As the maximal value of $v_{\text {R}}$ is 1, the geometrical restriction does not affect droplets shorter than $L_{\text {D}}<=\varLambda _{\text {P}}+0.5W +L_{\text {J}}$. Neglecting both latter terms, we can articulate a robust rule for the construction of a microfluidic circuit with a modified junction. The rule states that droplets generated in the microfluidic system must be shorter than the length of the bypass $\varLambda _{\text {P}}$. This establishes the design guidelines of both the droplets generator and the junction.

Taking into account the maximal length of the ‘protrusion’ and the dynamic limitation given by Eq. (14), we obtain the limit of Ca for the non-break-up mode:

$$\begin{aligned} Ca \le \frac{\beta }{(L_{\text {D}}/W-L_{\text {J}}/W)v_{\text {R}}-l_0}. \end{aligned}$$

(18)

This relation sets the maximal limit for the Capillary number at which a droplet of length $L_{\text {D}}$ is not broken at a given $v_{\text {R}}$. Notice that the value of $v_{\text {R}}$ depends on the number of droplets introduced to the loop device (see Eq. 8 and the discussion there). Thus, depending on the resistance of a single droplet, there is a critical number of droplets in the loop above which the next droplet entering the junction breaks. Hence, appropriate adjustment of both the frequency of droplets and the value of Ca avoids the appearance of droplet’s breakage in the microfluidic system (compare Fig. 4a and b).

The above-mentioned experimental analysis of the limits of the non-break-up mode shows that the modified junction can work correctly in a wide range of parameters. However, the knowledge of these limitations is crucial for the proper design of the microfluidic device.

3.6 Improving the junction for multi-directional flows

Fig. 11

The behaviour of the long droplet in different junctions with reversed flow—two inputs and one output. The sequence of consecutive snapshots for: left column—type J1 and right column—type J2. For both cases, the output flow is the same and $Q_{\text {OUT}} = 1 \ {\text {ml/h}}$

As for now, we investigated only one type of modified junction (type J1). In Fig. 1, we presented additionally the geometries of other types of junctions. In this section, we discuss additional possible modifications of the junction and their effect on the functionality of the microfluidic architecture.

Let us consider the end of the loop where two branches join forming a joining junction. The configuration of flows in this junction is inverted in relation to the previously considered dividing junction. The joining junction merges two input flows into one output flow unlike the dividing junction, which splits the one input flow between two outlets. Herein, we consider the additional possible scenario where the droplet from one of the branches of the loop enters the joining junction. Our observations of the regular junction (type J0) and the other one with one bypass (type J1) revealed that once the droplet enters the common channel its front starts to move with a higher speed than the rear part. This usually results in the break-up of the droplet (see Fig. 11, the left column for junction type J1). Indeed, in the case of the joining junction, the speed in the common channel is the sum of speeds in both input channels. This speed difference is responsible for the splitting of the droplet.

Figure 11 shows examples of the different behaviours of a long droplet in the junction type J1 and junction type J2 for the inverted flow configuration. The observations revealed that to keep the integrity of the droplet, an additional bypass must be introduced into the geometry of the junction. For example, to avoid the split of the droplet entering the junction from the right branch, a junction of type J2 should be applied (see Fig. 11 the left column). To increase the functionality and allow as well droplets from the left branch to travel through the branch in one piece, we need to use another additional bypass as in junction type J3.

3.7 Examples

To demonstrate the potential use of the modified junctions in microfluidic devices, we present two examples of small microfluidic geometries with different functionalities.

The first device is presented in Fig. 12. The central part of the device is a small symmetrical loop with two identical junctions of type J2 on both ends of the loop depicted as B1 and B2. The additional traps A1 and A2 are to limit the movement of the droplet. The trap stops the incoming droplet but it releases the droplet after the change of the flow direction. The operation mechanism of these traps was described before (Korczyk et al. 2013; Zaremba et al. 2018). The additional junction C exists only for the generation of a single droplet. After the droplet is in the device, this junction is inactive.

Commencing the description of the functionality of the device from the upper left image. A single droplet has been already generated and moved into trap A1. The flow of the CP is from the right to the left (as indicated by blue arrows). This is the stationary state of the device as the droplet is immobilized. This can be changed by the reversal of the flow direction—see the upper right image (the green arrows indicate the order of the snapshots). The flow of the CP from the left to the right removes the droplet from trap A1, then the droplet travels toward the loop and turns left into the upper branch. This direction is fixed by the geometry of the junction of type J2. Then, the droplet meets the other junction of type J2 at the end of the loop. As we mentioned in the previous section, the special design of the junction keeps the integrity of the droplet either in the inlet to the loop or in the outlet. Finally, the droplet stops in trap A2 (see the bottom right image) and the system reaches its second stationary state. The rotational symmetry of the device implies that after the next flow reversal of the CP (to its initial direction), the droplet will travel a symmetrical route, now through the bottom branch of the loop. In this example, the oscillating flow of the CP is translated to the circulation of the droplet inside the loop. Such a mechanism can be used for the implementation of loop-like laboratory sequences of droplet operations (Debski et al. 2018; Abolhasani and Jensen 2016).

This example teaches as well that the character of the flow of the droplets may be very different than the case of single-phase flow. In the case of single-phase flow at low Reynolds numbers, we can expect the time reversibility of the flow. In the case of the flow of the droplet, we observed that the droplet travels through the upper branch of the loop or through the bottom branch depending on the direction of the input flow of the CP.

In the second example, presented in Fig. 13, we use a constant flow of the CP without changing its direction. In this example, we consider two droplets entering the loop device. The device here is not symmetrical. Each of the branches of the loop consists of an additional element—an obstacle. It is a local constriction of the channel’s cross section. The flow is from the left to the right. Without any droplet in the loop, the flow of the CP splits into equal parts between the two branches (Fig. 13a). As we mentioned before, the modification of the junction weakly influences single-phase flow. The obstacles in both branches equally increase the hydraulic resistance.

The flow distribution between both branches can be quantified by the coefficient $v_{\text {L}}=V_{\text {L}}/V_{\text {IN}}$, previously introduced in the description of the flow of small droplets in loop devices. In this case, we can state that for the flow of the CP and without any droplet in the device $v_{\text {L}}(0)=0.5$.

The situation changes after the first droplet enters the device. The junction routes the droplet into the left branch, where it meets the obstacle. To pass through the obstacle, the front of the droplet would require to produce a high curvature to penetrate the constriction of the channel that needs an additional pressure increase—above the specific breakthrough pressure. However, if the flow of the CP through the right branch generates a pressure drop lower than the breakthrough pressure, the droplet will be kept immobilized. A similar mechanism of immobilization is known from microfluidic traps (Korczyk et al. 2013; Zaremba et al. 2018).

In this configuration, the whole CP flows only through the right branch as the left one is closed by the immobilized droplet (see Fig. 13b). This clearly shows that the droplet changes the state of the flow. Now, the coefficient of distribution of the flow can be estimated as $v_{\text {L}}(1)=0$ (no flow through the left branch). This value is below $v_{\text {Lcrit}}$; hence, we can expect that the next droplet will be directed into the right branch. Indeed, the next droplet entering the loop chooses the right channel; however, something very interesting happens once the second droplet reaches the obstacle. In this situation, the flow of the CP can no longer bypass both droplets; hence, the pressure behind the droplets increases above the breakthrough pressure needed to push the droplets over the obstacles. The pressure acts on both droplets so they are finally released and travel toward the exit of the loop (see Fig. 13c). The important feature of this device is that both obstacles are placed in different positions. Both droplets are triggered simultaneously but have different distances to the exit of the loop. In result, the second droplet leaves the device before the first droplet (see Fig. 13d). This simple device changes the order of the droplets. The mechanism utilized in this example can be used in other devices performing logic operations on the flowing droplets.

Fig. 12

Circulating loop. Four snapshots representing the complete cycle of circulation of the droplet. Green arrows indicate the order of the sequence. Top left: the stationary state for the flow to the left; the droplet is immobilized in the trap A1. B1 and B2 are two symmetric junctions connecting both branches of the central loop with the main channel. A2—the other trap symmetrical to trap A1. C—the additional channel enabling the generation of the single droplet (not used once the droplet is introduced). Top right: the transitional state after the reversal of the flow direction. The droplet is removed from the trap, moves to the right according to the reversed flow. In junction B1, it turns left and travels through the top branch of the loop to eventually stop in the trap A2. Bottom right: the stationary state for the flow to the right, with the droplet immobilized in trap A2. Bottom left: the transient state after reversing the flow restoring its initial direction. Droplet travels through the bottom branch of the loop to stop in trap A1 (as shown in the top left snapshot) completing a full cycle of the circulation. (Color figure online)

Fig. 13

The microfluidic device rearranging the order of droplets in the sequence. a The micrograph of the device without droplets. The flow of the CP is constant—from the left to the right. The junction in the inlet to the loop is of the type J1. The crucial elements are obstacles placed in both branches of the device. In the absence of droplets, the flow of CP is distributed equally between two branches as indicated schematically by bifurcated red arrows. b The first droplet (coloured by green) enters the upper branch, stops at the obstacle and blocks the flow of the CP through the upper branch. c The second droplet (blue) enters the bottom branch and triggers the release of the first droplet. d Both droplets leave the loop with their order changed (the blue droplet goes as the first one). (Color figure online)

4 Conclusions

In this paper, we investigated the behaviours of droplets in junctions modified by additional bypasses. In a series of experiments, we showed the effect of the modifications on both short and long droplets. Our observations revealed that the bypasses in the junctions can be used for guiding droplets to the preferred output and for the preventing of the break-up of long droplets. We provided an experimental analysis of the process of droplet transfer through the junction, which explains the peculiar behaviour of the droplets. This analysis revealed that the droplet is a subject of nontrivial transformation, which resembles the so-called ‘Baker transform’. We showed as well that the break-up of droplets can be explained by a simple model.

These modified junctions can be used in microfluidic systems where the motion of droplets is determined by the geometry of the device. This enables the encoding of a sequence of operations on droplets in the architecture of the device. Examples of simple microfluidic modules with non-trivial functions show the potential use of this approach.