Capillary focusing close to a topographic step: shape and instability of confined liquid filaments

Abstract

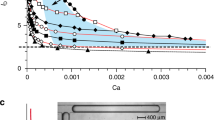
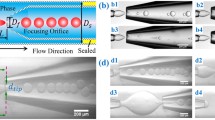
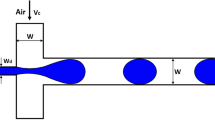
Step-emulsification is a microfluidic technique for droplet generation which relies on the abrupt decrease of confinement of a liquid filament surrounded by a continuous phase. A striking feature of this geometry is the transition between two distinct droplet breakup regimes, the “step-regime” and “jet-regime,” at a critical capillary number. In the step-regime, small and monodisperse droplets break off from the filament directly at a topographic step, while in the jet-regime a jet protrudes into the larger channel region and large plug-like droplets are produced. We characterize the breakup behavior as a function of the filament geometry and the capillary number and present experimental results on the shape and evolution of the filament for a wide range of capillary numbers in the jet-regime. We compare the experimental results with numerical simulations. Assumptions based on the smallness of the depth of the microfluidic channel allow us to reduce the governing equations to the Hele-Shaw problem with surface tension. The full nonlinear equations are then solved numerically using a volume-of-fluid-based algorithm. The computational framework also captures the transition between both regimes, offering a deeper understanding of the underlying breakup mechanism .