Abstract
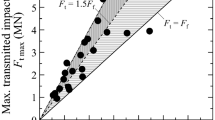
A series of the experiments was conducted to understand the effect of weight, size, shape, stiffness, material of collision object, and type of movement of collision object on mobilization characteristics of impact force. Results from the element rockfall test, rockfall test using slope model, are introduced in the paper. The relationships between the maximum amplitude of the impact force and the momentum were highly scattered depending on the shape, stiffness, constituent material, and type of the movement of the collision object. On the other hand, the results obtained from the tests indicated that the relationships between force product and momentum of the impact load can be expressed by single linear equation with high coefficient of determination although the test conditions were largely different. The knowledge obtained from the reduced scale tests, which are element rockfall test and rockfall test using slope model, extended to the prototype scale by referring to the results of the dynamic centrifuge model test and pendulum test conducted by authors and others. By reflecting these knowledges, a concept of the energy-based design approach, which makes it possible to rationalize the design of the protection wall for rockfall and sliding soil mass, is also proposed.























Similar content being viewed by others
References
Abe K, Nakamura S (2017) Suggestion of evaluation methods of impact loads of rocks and soils based on a series of model experiments, Proc of the 19th International conference on soil mechanics and foundation engineering
Buzzi O, Giacomini A, Spadari M (2012) Laboratory investigation on high values of restitution coefficients. Rock Mech Rock Eng 45(1):35–43
Chikatamarla R, Laue J, Sarah MS (2004) Rockfall impact on protection galleries, second international conference of structural engineering mechanics and computations. Balkema, Rotterdam
Francesco C, di Claudio P, Mauro V (2005) Experimental and numerical study of rock-fall impacts on granular soils. Rivista Italiana di Geotechnica 39(1):95–109
Glover JMH (2015) Rock-shape and its role in rockfall dynamics (Doctoral dissertation, Durham University)
Hertz HZ (1882) On contact between elastic solids, Gsammelte Werke, Vol. 1, Leipzig, Germany
Japan Road Association (2017) Manual of countermeasures for rock fall
Kwan JSH, Chan SL, Cheuk JCY, Koo RCH (2014) A case study on an open hillside landslide impacting on a flexible rockfall barrier at Jordan Valley, Hong Kong. Landslides 11(6):1037–1050
Labiouse V, Heidenreich B (2009) Half-scale experimental study of rockfall impacts on sandy slopes. Nat Hazards Earth Syst Sci 9(6):1981
Lambert S, Kister B (2018) Efficiency assessment of existing rockfall protection embankments based on an impact strength criterion. Eng Geol 243:1–9
Mavrouli O, Corominas J (2010) Vulnerability of simple reinforced concrete buildings to damage by rockfalls. Landslides 7(2):169–180
Nakajima S, Koseki J, Watanabe K, Tateyama M (2009) A simplified procedure to evaluate earthquake-induced residual displacements of conventional type retaining walls. Soils Found 49(2):287–303
Nakajima S, Abe K, Shinoda M, Nakamura S, Nakamura H, Chigira K (2019) Dynamic centrifuge model tests and material point method analysis of the impact force of a sliding soil mass caused by earthquake-induced slope failure. Soils Found 59(6):1813–1819
Nakamura S, Abe K, Wanatabe K, Nakajima S (2018) Analysis of flow and impact behavior based on existing cascading experiment of collapsed soil and reproduction analysis by MPM. J Jpn Soc Civil Eng Ser C (Geosphere Engineering) 74(3):259–274 (in Japanese)
Nakamura S, Wakai A, Umemura J, Sugimoto H, Takeshi T (2014) Earthquake-induced landslides: distribution, motion and mechanisms. Soils Found 54(4):544–559
Nakano M, Ukon N (1986) Experiment on the impact force of collapsed sandy soil mass. J Jpn Soc Erosion Control Eng 39(1):17–23
Nakatsutsumi J, Tani K (1982) Experimental study of impact due to free fall sand. Proceedings of the Japan Society of Civil Engineers 1982:119–127
Nishida Y, Inoue S, Yoshida M, Sawada K, Yashima A (2006) Actual impact test on full scale type model of rock fall protection MSE wall and concrete wall. 41th Ann Cong Jpn Geotech Soc:2237–2238
Nishimura S, Takeshita Y, Nishiyama S, Suzuki S, Shibata T, Shuku T, Komatsu M, Kim B (2020) Disaster report of 2018 July heavy rain for geo-structures and slopes in Okayama, Soils and Foundations (in press)
Peila D, Oggeri C, Castiglia C (2007) Ground reinforced embankments for rockfall protection: design and evaluation of full scale tests. Landslide 4:255–265
Perret S, Dolf F, Kienholz H (2004) Rockfalls into forests: analysis and simulation of rockfall trajectories—considerations with respect to mountainous forests in Switzerland. Landslides 1(2):123–130
Railway Technical Research Institute (2012) Design standard for railway structure -retaining structure-. Maruzen, Tokyo
Volkwein A, Schellenberg K, Labiouse V, Agliardi F, Berger F, Bourrier F, Dorren LKA, Gerber W, Jaboyedoff M (2011) Rockfall characterization and structural protection – a review, natural hazards and earth system science. Science 11:2617–2651
Wang B, Cavers DS (2008) A simplified approach for rockfall ground penetration and impact stress calculations. Landslides 5(3):305
Watanabe K, Koseki J, Tateyama M (2005) Application of high-speed digital CCD cameras to observe static and dynamic deformation characteristics of sand. Geotech Test J ASTM 28(5):423–435
Yu BYW, Zhao H (2018) Experimental study on the maximum impact force by rock fall. Landslide 15:233–242
Yu ZX, Zhao L, Liu YP, Zhao SC, Xu H, Chan SL (2019) Studies on flexible rockfall barriers for failure modes, mechanisms and design strategies: a case study of Western China. Landslides 16(2):347–362
Zhong MJ, Zhi JC, Qing HN, Tian JW, Hao S, Ting HW (2019) Laboratory study on the infuluencing factors and their control for the coefficient of restitution during rockfall impact. Landslides 16(10):1939–1963
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nakajima, S., Abe, K., Shinoda, M. et al. Experimental study on impact force due to collision of rockfall and sliding soil mass caused by seismic slope failure. Landslides 18, 195–216 (2021). https://doi.org/10.1007/s10346-020-01461-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10346-020-01461-z