Abstract
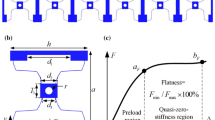
In this paper, a tunable locally resonant metamaterial is proposed for low-frequency band gaps. The local resonator composed of two pairs of folded slender beams and a proof mass is designed based on the theory of compliant mechanism. The design optimization on geometric parameters is carried out to fulfil the quasi-zero-stiffness property. The locally resonant metamaterial is formed by periodically arranged unit cells, and the transmittance of longitudinal wave is studied through three aspects: numerical predictions, finite element simulations and experimental tests. The variation trends revealed by these three methods match well with one another: the band gap moves to lower frequency and both its depth and width get smaller and smaller with the increase of pre-compression (\(\Delta \)). The band gap overlays the frequency range of 73.10–92.38 Hz and 16.78–19.49 Hz at \(\Delta = 0 \, \hbox {mm}\) and \(\Delta = 10 \, \hbox {mm}\), respectively, providing a wide range of tunability. Besides, the ultralow-frequency band gap can be achieved as \(\Delta \) approaches 10 mm. This study may provide an avenue for achieving the tunable ultralow-frequency locally resonant band gap.







Similar content being viewed by others
References
Chen JS, Sun CT. Wave propagation in sandwich structures with resonators and periodic cores. J Sandw Struct Mater. 2013;15:359–74.
Wang T, Sheng M, Ding X, Yan X. Wave propagation and power flow in an acoustic metamaterial plate with lateral local resonance attachment. J Phys D Appl Phys. 2018;51:115306.
Liu W, Yi B, Yoon GH, Choi H. Functionally graded phononic crystals with broadband gap for controlling shear wave propagation. Adv Eng Mater. 2020:2000645.
Sun JH, Wu TT. Propagation of acoustic waves in phononic-crystal plates and waveguides using a finite-difference time-domain method. Phys Rev B. 2007;76:104304.
Khelif A, Choujaa A, Benchabane S, Djafari-Rouhani B, Laude V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl Phys Lett. 2004;84:4400.
Yu D, Wen J, Zhao H, Liu Y, Wen X. Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid. J Sound Vib. 2008;318:193–205.
Nateghi A, Sangiuliano L, Claeys C, Deckers E, Pluymers B, Desmet W. Design and experimental validation of a metamaterial solution for improved noise and vibration behavior of pipes. J Sound Vib. 2019;455:96–117.
Yu D, Wen J, Shen H, Xiao Y, Wen X. Propagation of flexural wave in periodic beam on elastic foundations. Phys Lett A. 2012;376:626–30.
Zhu R, Huang GL, Hu GK. Effective dynamic properties and multi-resonant design of acoustic metamaterials. J Vib Acoust. 2012;134:031006.
Cai C, Zhou J, Wu L, Wang K, Xu D, Ouyang H. Design and numerical validation of quasi-zero-stiffness metamaterials for very low-frequency band gaps. Compos Struct. 2020;236:111862.
Qureshi A, Li B, Tan KT. Numerical investigation of band gaps in 3D printed cantilever-in-mass metamaterials. Sci Rep. 2016;6:28314.
Balaji PS, Karthik SelvaKumar K. Applications of nonlinearity in passive vibration control: a review. J Vib Eng Technol. 2020.
An X, Lai C, Fan H, Zhang C. 3D acoustic metamaterial-based mechanical metalattice structures for low-frequency and broadband vibration attenuation. Int J Solids Struct. 2020;191–192:293–306.
Zhao H, Wen J, Yu D, Wen X. Low-frequency acoustic absorption of localized resonances: Experiment and theory. J Appl Phys. 2010;107:023519.
Fan H, Yang L, Tian Y, Wang Z. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos Struct. 2020;243:112244.
Wang K, Zhou J, Wang Q, Ouyang H, Xu D. Low-frequency band gaps in a metamaterial rod by negative-stiffness mechanisms: Design and experimental validation. Appl Phys Lett. 2019;114:251902.
Ren T, Liu C, Li F, Zhang C. Active tunability of band gaps for a novel elastic metamaterial plate. Acta Mech. 2020;231:4035–53.
Zhou W, Chen W, Chen Z, Lim CW. Actively controllable flexural wave band gaps in beam-type acoustic metamaterials with shunted piezoelectric patches. Eur J Mech A Solid. 2019;77:103807.
Zhu R, Huang GL, Huang HH, Sun CT. Experimental and numerical study of guided wave propagation in a thin metamaterial plate. Phys Lett A. 2011;375:2863–7.
Zhu R, Liu XN, Hu GK, Sun CT, Huang GL. A chiral elastic metamaterial beam for broadband vibration suppression. J Sound Vib. 2014;333:2759–73.
Wang T. Tunable band gaps in an inertant metamaterial plate with two-degree-of-freedom local resonance. Phys Lett A. 2020;384:126420.
Zhang Q, Zhang K, Hu G. Tunable fluid-solid metamaterials for manipulation of elastic wave propagation in broad frequency range. Appl Phys Lett. 2018;112:221906.
Wang K, Zhou J, Xu D, Ouyang H. Tunable low-frequency torsional-wave band gaps in a meta-shaft. J Phys D Appl Phys. 2019;52:055104.
Wang P, Casadei F, Shan S, Weaver JC, Bertoldi K. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Phys Rev Lett. 2014;113:014301.
Lan CC, Lee KM. Generalized shooting method for analyzing compliant mechanisms with curved members. J Mech Design. 2006;128:765–75.
Lan CC, Wang JH, Chen YH. A compliant constant-force mechanism for adaptive robot end-effector operations. Proc IEEE Int Conf Robot Autom. 2010:2131–6.
Lan CC, Cheng YJ. Distributed shape optimization of compliant mechanisms using intrinsic functions. J Mech Design. 2008;130:072304.
Acknowledgements
The authors gratefully acknowledge the support from the National Natural Science Foundation of China (11972152, 11832009), the National Key R&D Program of China (2017YFB1102801), and the Laboratory of Science and Technology on Integrated Logistics Support.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Declarations of Interest
The authors declare no conflict of interest.
Rights and permissions
About this article
Cite this article
Lin, Q., Zhou, J., Pan, H. et al. Numerical and Experimental Investigations on Tunable Low-frequency Locally Resonant Metamaterials. Acta Mech. Solida Sin. 34, 612–623 (2021). https://doi.org/10.1007/s10338-021-00220-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10338-021-00220-4