1 Introduction

The complex geometries and materials developed in biological systems possess unique mechanical properties. These systems have inspired the development of bioprinting and metamaterial manufacturing and have attracted widespread attention in engineering fields [1,2,3]. Through centuries of evolution and optimization, nature provides an excellent source of inspiration for metamaterials, which has inspired scholars to design and explore multi-functional metamaterials.

Lattice metamaterials are emerging as popular research subjects. This has been greatly promoted by additive manufacturing technology. Lattice metamaterials are obtained using artificially designed unit cells in periodic arrays in one, two, or three dimensions. They have great potential for practical applications, such as vibration filtering [4], creating materials with adjustable Poisson’s ratios [5], and waveguide design [6,7,8,9]. Lattice metamaterials exhibit unique mechanical, thermal, and vibrational properties, which have been the subject of numerous analytical, numerical, and experimental studies [10,11,12]. In particular, their unique vibrational properties, including band gaps and directional wave propagation characteristics, are the main outstanding features. These properties can be used to control and manage wave propagation and vibration suppression. For example, artificially designed pentamode materials have the advantages of wide bands, solid states, and high transmission rates, and they have certain application value for controlling low-frequency underwater sound [13, 14]. Recently, many studies have been conducted on lower band gaps and methods to reduce the band gap and increase the band gap width [15]. The topological characteristics of the designed structure have important effects on the positions and widths of band gaps [16]. Several extensive studies have been conducted on the application of combined band gaps and directional characteristics of periodic structures, such as two-dimensional hexagons, auxetic chiral lattices, octa-chiral lattices, and surface lattices [17,18,19,20].

In recent years, mechanical metamaterials inspired by biological systems have become very attractive, creating new opportunities for the combination of mechanics and biology [21,22,23]. Among these metamaterials, the chiral metamaterials inspired by DNA have great static and dynamic properties and good designability and tunability and can be used as impact energy absorbers and mechanical logic switches [24]. Additionally, the bio-nano-networks composed of microtubules can control and absorb harmful vibrations and exhibit good dynamic performances, and thus, they can be applied to the design and development of the next-generation biomechanical instruments [25]. Hierarchical cellular materials are also introduced into periodic structures for vibration control and related multi-functional design [26]. Furthermore, many researchers have explored wave propagation dispersion by fractal or quasi-fractal structures. An optimized typing technique can be used to create wide band gaps, which confirms the significant advantages of fractal geometries in terms of band gap generation [27, 28]. A periodic structure with a Sierpinski carpet has the characteristics of a directional waveguide, which can further expand the field of vibration reduction [29]. The Hilbert fractal, inspired by nature, was used to design acoustic metamaterials with negative effective densities that could generate multiple band gaps in the subwavelength range, making engineering design in the subwavelength range possible [30, 31]. Although the above analysis of the fractal geometry is limited to the propagation of plane waves in periodic plates, the exploration of fractal periodic beams, plates, and shells deserves further study.

The introduction of fractal geometry has a significant influence on the dynamic characteristics of lattice metamaterials, and Koch fractals can be used to design the fractal geometry [32]. In this study, inspired by the Koch fractal topology, lattice metamaterials with different numbers of iterations were designed to study the wave propagation characteristics, as the Koch fractal can potentially tune the band gap and directional wave propagation. We first investigated the band structure of the proposed lattice metamaterial using Bloch’s theorem and the finite element method. The accuracy of the model was verified through dynamic response simulations of the finite structure. We also used the group velocity and numerical simulations to predict the directional characteristics of lattice metamaterials with Koch fractals. Furthermore, the effect of Koch fractal on wave propagation was also studied in terms of the band gap of desired frequency position by adjusting the geometric parameters of the Koch fractal.

The remainder of the paper is organized as follows. In Sect. 2, brief descriptions of the lattice metamaterials with Koch fractals are given, and dynamical models are established. In Sect. 3, the band structures and group velocities of lattice metamaterials with different Koch fractal iterations are presented, and the results are verified by finite element simulations. The effects of the parameters and geometric topologies on the band structure are studied. Finally, Sect. 4 summarizes the important conclusions of this study.

2 Characterization of Lattice Metamaterials with Koch Fractal

2.1 Geometric Parameters of Lattices

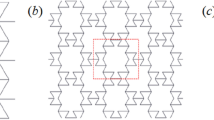
In this study, we converted conventional straight beams in lattice metamaterials with Koch fractals. Although many periodic configurations have been reported in the literature [33], they share some basic common features. A lattice metamaterial with Koch fractals was designed with a square configuration. In this structure, the fractal named by Mandelbrot [34] can be used to design complex forms through simple algorithms, and the Koch fractal was one of the first mathematically described fractals. It is generated by an iterated function with the number of iterations defined as N. The Koch fractal is initiated (at zero iteration, \(N=0\)) from a straight line with the length of \(a_{0} \). In the first iteration (\(N=1\)), the middle segment of the line is replaced by two segments with the same lengths rotated upward by 60°, and the total length of the curve is \(\frac{4}{3}a_{0} \), as shown in Fig. 1a. The relationship between the total length of the Koch fractal and the number of iterations N can be defined as \(L_{N} =a_{0} \times \left( {\frac{4}{3}} \right) ^{N}\). Thus, to satisfy the definition of the Koch fractal, the smallest length \(a_{N} \) of the \(N^{\mathrm {th}}\)-order Koch fractal is related to \(a_{0} \) and N as follows:

$$\begin{aligned} a_{N} =a_{0} /3^{N} \end{aligned}$$
(1)

The total length of the Koch fractal can be expressed as follows:

$$\begin{aligned} L_{N} =a_{0} (4 / 3)^{N}=4^{N}a_{N} \end{aligned}$$
(2)

Equation (2) shows that the total arc length \(L_{N}\) grows exponentially with N.

Assuming that the lattice constant is a, the initial length \(a_{0} =a/2\). The slenderness ratio of the beam is \(\lambda \). The cross section of the beam is rectangular, and the height of the beam is constant, \(h=\frac{a}{2\lambda }\). The initial width of the beam is determined by the slenderness ratio, defined as \(d_{0} =\frac{a}{2\lambda }\). Under the mass equivalence assumption, the width of a lattice metamaterial with Koch fractals can be calculated as follows:

$$\begin{aligned} d=d_{0} \times 2\times a/L_{n} \end{aligned}$$
(3)
Fig. 1
figure 1

Lattice metamaterials with Koch fractals with different iteration numbers: a Koch fractal designs for \(N=0\), 1, 2, and 3; b unit cell of the lattice with \(N=0\) and c square lattice

Full size image

Figure 1b, c depicts a square lattice with a Koch fractal. By repeating the unit cell in the x- and y-directions, a 2D periodic structure can be formed. As the structure is assembled with slender beams, we select the Timoshenko beam model to calculate the structural dynamic response [35]. The material parameters are assumed to be: Young’s modulus \(E=200~\hbox {GPa}\), Poisson’s ratio \(\nu =0.3\), and mass density \(\rho =7850~\hbox {kg m}^{-3}\).

2.2 Bloch’s Theorem

The main advantage of Bloch’s theorem is that the dynamic performance of the whole structure can be determined by analyzing the unit cell. The use of Bloch’s theorem to study wave propagation in periodic systems has greatly improved the computational efficiency and reduced the computational costs. According to this theorem, the displacement of a point P in the \(\left( {n_{1} ,n_{2} } \right) \) cell can be expressed in terms of the displacement of the corresponding point in the reference cell as follows:

$$\begin{aligned} w\left( {r_{P}^{n_{1} ,n_{2} } } \right) =w(r_{P}^{0,0} )\hbox {e}^{\left( {n_{1} k_{1} +n_{2} k_{2} } \right) } \end{aligned}$$
(4)

where \(k_{1} \) and \(k_{2} \) denote the wavenumbers, and \(r_{P}^{n_{1} ,n_{2} } \) is the displacement of point P. Equation (4) implies that the wave propagation behavior of a periodic system can be identified through the investigation of the reference unit cell.

2.3 Dynamic Modeling of Unit Cell

It is critical to establish a dynamic model of the periodic structure to investigate the propagation of waves in the periodic lattice. Because the lattice metamaterials with Koch fractals are assembled with slender straight beams and thus have organizational regularity, the finite element method is selected to establish a dynamic model of the unit cell. We first determine the dispersion relation of the square lattice. The unit cell is considered to be a combination of rigidly connected Timoshenko beams. Using a standard discretization process [35], the kinetics equation of the unit cell can be expressed as follows:

$$\begin{aligned} \left( {{\varvec{K}}-\omega ^{2}{{\varvec{M}}}} \right) {{\varvec{q}}}={{\varvec{F}}} \end{aligned}$$
(5)

where K and M donate the global stiffness and mass matrix, \(\omega \) is the angular frequency, and q and F are the vectors of node displacements and forces, respectively. For the unit cell in a square lattice shown in Fig. 2a, the displacement vector can be written in the following form:

$$\begin{aligned} {{\varvec{q}}}=\left\{ {{\begin{array}{*{20}c} q_{l} &{} q_{r} &{} q_{b}&{} q_{t} &{} q_{i} \\ \end{array} }} \right\} ^{\mathrm{T}} \end{aligned}$$
(6)

where the subscripts l, r, b, t, and i denote the displacements corresponding to the left, right, bottom, top, and internal nodes of a unit cell, respectively, as shown in Fig. 2a.

Fig. 2
figure 2

a Degrees of freedom of the unit cell; b first Brillouin zone and irretrievable Brillouin zone

Full size image

According to Bloch’s theorem, periodic boundary conditions that include the reference unit cell’s generalized displacements and the equilibrium conditions of the generalized forces can be expressed as follows:

$$\begin{aligned} {\begin{array}{*{20}c} {q_{r} =\text {e}^{k_{1} }q_{l} ,} &{} {q_{t} =\text {e}^{k_{2} }q_{b} } \\ \end{array} } \end{aligned}$$
(7)

Equation (7) states that the displacement of the right end of the unit cell structure can be expressed by the displacement of the left end and the corresponding periodic conditions. Similarly, the displacement of the top end can be expressed by the displacement of the bottom end and the corresponding periodic conditions. Equation (7) can be rewritten in matrix form as follows:

$$\begin{aligned} {{\varvec{u}}}={{\varvec{Aq}}}_{r} \end{aligned}$$
(8)

where \({{\varvec{q}}}_{r} =\left\{ {{\begin{array}{ccc} {q_{l} } &{} {q_{b} } &{} {q_{i} } \\ \end{array} }} \right\} ^{\mathrm{T}}\). Substituting Eq. (8) into Eq. (5), and assuming \({{\varvec{F}}}={\mathbf{0}}\), yields the following:

$$\begin{aligned} \left[ {{{\varvec{K}}}_{r} \left( {k_{1} ,k_{2} } \right) -\omega ^{2}{{\varvec{M}}}_{r} \left( {k_{1} ,k_{2} } \right) } \right] {{\varvec{q}}}_{r} ={\mathbf{0}} \end{aligned}$$
(9)

where \({{\varvec{K}}}_{r} (k_{1} ,k_{2} )\) and \({{\varvec{M}}}_{r} (k_{1} ,k_{2})\) are the reduced stiffness and mass matrices, respectively. Equation (9) is an eigenvalue problem whose solution defines the dispersion characteristics of the lattice. In general, the wavenumbers \(k_{1} \) and \(k_{2} \) along the contour of the irreducible region of the first Brillouin region (Fig. 2b) are limited to determine the frequency \(\omega \). By solving Eq. (9), the band structure is obtained for the given \(k_{1} \) and \(k_{2} \), which could be used to evaluate the dispersion characteristics.

Moreover, the group velocity defines the directionality of the elastic wave propagation and the anisotropic characteristics of the periodic structure. The directional characteristics of elastic waves extend the applications of periodic structures for vibration isolation. Thus, it is important to study the directionality of wave propagation by directly assessing the group velocity.

The wave direction characteristics of the lattice are provided by the group velocity, which can be expressed as follows:

$$\begin{aligned} {{\varvec{c}}}_{g} =\left( {\frac{\partial \omega }{\partial k_{1} },\frac{\partial \omega }{\partial k_{2} }} \right) ^{\mathrm{T}} \end{aligned}$$
(10)

The dispersion behaviors are highlighted by the frequency-dependent group velocity, which describes the anisotropy of the domain in the plane wave propagation. In the following section, the calculated band structures and group velocities are discussed for lattice metamaterials with Koch fractals.

3 Results and Discussion

To directly compare the wave propagation behaviors of the lattice metamaterials with different iteration numbers, the frequency values are presented in terms of the normalized frequency \(\Omega \), which is defined as \(\Omega =\frac{\omega a}{2\pi c}\), where a is the lattice constant, and \(c=\sqrt{E/\rho } \) is the velocity of the longitudinal wave in the material.

3.1 Band Structures of Square Lattice Metamaterials

The band structures of lattice metamaterials are discussed first in this section. Figure 3 shows the band structure of the lattice metamaterials with different numbers of iterations. There is no band gap in the band structure with \(N=0\), as shown in Fig. 3a. For the case of \(N=1\), three full band gaps appear in the band structure. Two large band gaps appear from \(\Omega =0.477\) to 0.525 and from \(\Omega =1.354\) to 1.432, and the width of the first band gap is 0.048. For the case of \(N=2\), there are also three band gaps. Two large band gaps appear from \(\Omega =0.363\) to 0.453 and from \(\Omega =1.019\) to 1.111, and the width of the first band gap is 0.09. Thus, the band gap is greatly reduced. Furthermore, there are five band gaps for \(N=3\). The number of band gaps increases, while the frequency of the band gap decreases. The number of iterations of the lattice metamaterials with Koch fractals has a significant effect on the band structure. For \(N >0\), the lattice metamaterials with Koch fractals show multi-band gap characteristics, which is conducive to vibration suppression. As the number of iterations increases, the position of the first band gap decreases, which is helpful to achieve a lower band gap.

Fig. 3
figure 3

Band gap of the metamaterials with Koch fractals for iteration numbers of a \(N=0\), b \(N=1\), c \(N=2\) and d \(N=3\)

Full size image

In this section, we analyze the effects of geometric parameters on band structure. Figure 4a–c shows distributions of the band gaps of the lattice metamaterial with Koch fractals as functions of the slenderness ratio. There are no band gaps in the band structure when \(N=0\). When the number of iterations is greater than 0, band gaps appear. For the case of \(N=1\) or 2, three band gaps appear. The first and third band gaps have larger widths, and their widths and positions gradually decrease as the slenderness ratio decreases. There are five band gaps with a wider frequency range when \(N=3\). Vibration suppression can be achieved by multiple low-frequency bands. Moreover, the band gap decreases as the slenderness ratio decreases.

We further discuss the effect of slenderness ratio on the lowest band gap, as shown in Fig. 4d. With the decrease in the slenderness ratio, the minimum band gaps for different iteration numbers tend to decrease in width and position. The number of iterations of the Koch fractal has a significant effect on the distribution of band gap. As the number of iterations increases, the minimum frequency of the structure decreases. Based on the above analysis, the number of iterations can be used to adjust the number and position of the band gap. The slenderness ratio mainly influences the width of the band gap, which provides multiple methods to tune the band gaps to meet engineering needs.

Fig. 4
figure 4

Relationship between the band gap and the geometric parameters \(\lambda \) and N for a \(N=1\), b \(N=2\), and c \(N=3\); d lowest band gap of the structure with different geometric parameters

Full size image

3.2 Wave Transmission Spectra

To verify the band gap obtained by theoretical calculations, we also carry out numerical simulations of the vibrational characteristics of a typical finite structure using the commercial finite element software COMSOL to obtain the frequency response function (FRF). The finite structure contains \(50\times 50\) unit cells composed of Timoshenko beams with square cross sections. The mesh generator in COMSOL is used to build a finer triangular mesh to ensure mesh quality. The FRF is obtained by calculating the steady-state dynamic response of the lattice metamaterials with Koch fractals. The FRF is defined as a function of the non-dimensional frequency, which can be expressed as follows:

$$\begin{aligned} T=20\log _{10} \left( \frac{U_{\mathrm{res}} }{U_{\mathrm{exc}} }\right) \end{aligned}$$
(11)

where \(U_{\mathrm{exc}} \) and \(U_{\mathrm{res}}\) are the displacements of the excitation point and the response collection point, respectively. The transmission coefficient T provides useful information about the frequencies of the waves propagating throughout the structure. For example, a small value of T means that the wave propagation of the corresponding frequency is prohibited.

Figure 5 lists the FRF values for the lattice metamaterials with different numbers of iterations. When the iteration number \(N=0\), the FRFs have no evident attenuation region, corresponding to the band structure in Fig. 3a without a band gap. For \(N=1\), the frequency regions of the vibration attenuation in the FRF are [0.477, 0.525] and [1.354, 1.432]. These frequency attenuation regions are in good agreement with the band gap (calculated by theory), indicating that the amplitude of vibration is significantly reduced in the band gap range, as shown in Fig. 3b. When \(N>0\), the FRFs have multiple attenuation regions, and the attenuation values increase with the increase in the number of iterations, showing that the vibrations in this frequency region are greatly suppressed and attenuated. For \(N>0\), there are multiple attenuation ranges in the FRFs, indicating that the lattice metamaterials with Koch fractals expand the vibration damping area without increasing the unit cell size.

Fig. 5
figure 5

Frequency responses for lattice metamaterials with Koch fractals for different iteration numbers: \(N=0\), 1, 2, and 3

Full size image

3.3 Group Velocity

Figure 6 shows the group velocity of lattice metamaterials with Koch fractals for the first two iteration numbers at a given frequency, plotted with blue dotted lines in Fig. 3a, b. The amplitude of the group velocity is related to the preferential directions of wave propagation or the existence of “forbidding directions” along which the waves cannot propagate. The given frequency is within the limits of the shear wavelength. The group velocities of the first- and second-order frequencies are shown as green and blue dots in Fig. 6a, b. For \(N=0\), the group velocities are clearly concentrated in the x- and y-directions, indicating that an elastic wave at this frequency only propagates in the x- and y-directions but not diagonally, as shown in Fig. 6a. A relatively strong energy is concentrated in the direction of the propagating wave. In Fig. 6b, the shape of the group velocity at the second band is a diamond, indicating that lattice metamaterials cannot be considered isotropic. By comparing Fig. 6a with b, it is evident that the speed decreases as the number of iterations increases. The increasing number of iterations of the lattice metamaterial leads to a decrease in the structural stiffness, and therefore, the corresponding group velocity decreases.

Fig. 6
figure 6

Group velocities of lattice metamaterials with different numbers of iterations at a \(N=0\) and b \(N=1\); and the displacement fields for c \(N=0\) and d \(N=1\)

Full size image

The group velocity diagram and the displacement field under steady-state vibrations also show the propagation of vibrational energy. Therefore, we use the group velocity diagrams to analyze the wave propagation characteristics. The displacement field is calculated based on the finite period model to show the propagation of elastic waves. These two methods validate each other and can be used to describe the directional characteristics of wave propagation. Therefore, we study the response of the system to the harmonic rotation excitation at the center of the finite structure. The displacement field of the finite structure excited by simple harmonic rotational excitation is shown in Fig. 6c, d. The vibrational energy propagates along specific directions in the lattice metamaterials, which is consistent with the calculation results of group velocities.

3.4 Effect of Geometric Topologies

Although the results reported above are focused on lattice metamaterials with square topologies, the Koch fractal can be extended to other topologies, such as honeycombs. The band structures of honeycomb metamaterials with Koch fractals are shown in Fig. 7. As expected, in the honeycomb metamaterials with Koch fractals, low band gaps and multiple band gaps are still present. This proves that Koch fractals can generate multiple band gaps in lattice metamaterials. This phenomenon is completely different from that observed in traditional lattice materials, whose band gap characteristics are largely determined by lattice topology or node connectivity [4].

Fig. 7
figure 7

Band gap of honeycomb metamaterials with Koch fractal where the numbers of iterations are: a \(N=0\), b \(N=1\), c \(N=2\), and d \(N=3\)

Full size image

We compare the lowest band gaps of the honeycomb metamaterials with different numbers of iterations. The lowest band gap of the honeycomb metamaterial with Koch fractals is lower than that of the conventional honeycomb material. The slenderness ratio is critical for the position and width of the band gap, as shown in Fig. 8. As the slenderness ratio decreases, the width of the band gap decreases and the position also decreases, because the geometric parameters essentially determine the vibrational modes of lattice metamaterials.

Fig. 8
figure 8

Relationship between the lowest band gaps and the geometric parameter \(\lambda \)

Full size image

4 Conclusions

Lattice metamaterials with Koch fractals are investigated in detail. The band structures and group velocities of lattice metamaterials composed of Koch fractals with different iteration numbers are studied. The theoretical results are verified through finite element simulations, and the possibility of using lattice metamaterials with Koch fractals for vibration suppression and directional waveguide applications is confirmed. The proposed lattice metamaterial composed of Koch fractals has multiple and low band gaps. The number of iterations of the Koch fractal has a significant effect on the band gap, and these extraordinary band gap characteristics are inherently controlled by the artificially designed Koch fractal. Moreover, our results show that the proposed Koch fractal can be extended to a honeycomb topology. The lattice metamaterials with different numbers of iterations at a given frequency show unique directional characteristics. These observations reflect the unique tunability of lattice metamaterials with Koch fractals and provide new insights into the development of structured metamaterials and their potential applications.