Abstract
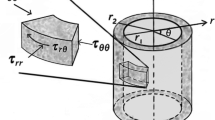
An analytical solution is obtained for transient torsional vibration of a finite hollow cylinder with initial axial stress. The cylinder is subjected to dynamic shearing stress at the internal surface and is fixed at the external surface. The basic equations are presented and the solution is obtained by means of Fourier series expansion technique and the separation of variables method. The effects of the initial stress on the natural frequencies and transient torsional responses are presented and discussed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Chattopadhyay, B., Torsional vibration of non-homogeneous isotropic hollow thick cylinder. Pure and Applied Geophysics, 1972, 97(5): 25–31.
Xie, S. and Liu, K., Transient torsional wave propagation in a transversely isotropic tube. Archive of Applied Mechanics, 1998, 68(9), 589–596.
Wang, X., Wang, X.Y. and Hao, W.H., An analytical solution for finitely long hollow cylinder subjected to torsional impact. Structural Engineering and Mechanics, 2005, 19(3): 281–295.
Rose, J.L., Ultrasonic Waves in Solid Media. Cambridge: Cambridge University Press, 1999.
Pan, J.Q. and Pan, J., Structural intensity of torsional vibration in solid and hollow cylindrical bars. Journal of the Acoustical Society of America, 1998, 103(3): 1475–1482.
Singh, B.M., Rokne, J. and Dhaliwal, R.S., Torsional vibration of functionally graded finite cylinders. Meccanica, 2006, 41(4): 459–470.
Kudliča, J., Dispersion of torsional waves in a thick-walled transversely isotropic circular cylinder of infinite length. Journal of Sound and Vibration, 2006, 294(1–2): 368–373.
Chen, W.T. and Wright, T.W., Frequency equations for wave propagation in an initially stressed circular cylinder. Journal of the Acoustical Society of America, 1966, 39(5):847–848.
Zhu, D.S., Qian, Q., Huang, Y.Y. and Zhu, S.S., Internal resonance of plate with initial stress. Acta Mechanica Solida Sinica, 1995, 16(2): 157–162 (in Chinese).
Aba-alla, A.M., The effect of initial stress and orthotropy on the propagation waves in a hollow cylinder. Applied Mathematics and Computation, 1999, 106(2–3): 237–244.
Liu, H., Kuang, Z.B. and Wang, T.J., Effect of initial stress on the propagation behavior of Love waves in a layered piezoelectric structure. International Journal of Solids and Structures, 2001, 38(1): 37–51.
Qian, Z., Jin F., Wang, Z. and Kishimoto, K., Love waves propagation in a piezoelectric layered structure with initial stresses. Acta Mechanica, 2004, 171(1–2): 41–58.
Du, J.K., Jin, X., Wang, J. and Zhou, Y., SH wave propagation in a cylindrically layered piezoelectric structure with initial stress. Acta Mechanica, 2007, 191(1–2): 59–74.
Cheng, C.Q. and Shen, Y.P., Stability analysis of piezoelectric circular cylindrical shells. ASME Journal of Applied Mechanics, 1997, 64(4): 847–852.
Author information
Authors and Affiliations
Corresponding author
Additional information
Projected supported by the National Natural Science Foundation of China (Nos. 10872179 and 10725210), the Zhejiang Provincial Natural Science Foundation of China (No. Y7080298) and the Zijin Plan of Zhejiang University.
Rights and permissions
About this article
Cite this article
Wang, H., Chen, W. Transient torsional wave in finite hollow cylinder with initial axial stress. Acta Mech. Solida Sin. 21, 536–541 (2008). https://doi.org/10.1007/s10338-008-0864-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10338-008-0864-8