Skip to main content
SpringerLink
Log in

Power Reflection and Transmission in Beam Structures Containing a Semi-Infinite Crack

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

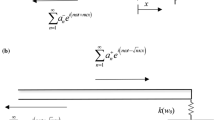
Wave reflection and transmission in a beam containing a semi-infinite crack are studied analytically based on Timoshenko beam theory. Two kinds of crack surface conditions: non-contact (open) and fully contact (closed) cracks, are considered respectively for an isotropic beam. The analytical solution of reflection and transmission coefficients for a semi-infinite crack is obtained. The power reflection and transmission ratios depend on both the frequency and the position of the crack. Numerical results show the conservation of power transport. The transmitted energy among various wave modes is also investigated. A finite element method is used to verify the validity of the analytical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wang, J.T.S., Lou, Y.Y. and Gibby, J.A., Vibration of split beams. Journal of Sound and Vibration, 1982, 84: 491–502.

    Article  Google Scholar 

  2. Rosalie, S.C., Vaughan, M., Bremner, A. and Chiu, W.K., Variation in group velocity of Lamb waves as a tool for the detection of delamination in GLARE aluminum plate-like structures. Composite Structures, 2004, 66: 77–86.

    Article  Google Scholar 

  3. Yan, Y.J. and Yam, L.H., Detection of delamination damage in composite plates using energy spectrum of structural dynamic responses decomposed by wavelet analysis. Computers and Structures, 2004, 82: 347–358.

    Article  Google Scholar 

  4. Lase, Y., Ichchou, M.N. and Jezequel, L., Energy flow analysis of bars and beams: theoretical formulations. Journal of Sound and Vibration, 1996, 192: 281–305.

    Article  Google Scholar 

  5. Pan, J., Ming, R., Hansen, C.H. and Cark, R.L., Experimental determination of total vibratory power transmission in an elastic beam. Journal of Acoustic Society of America, 1998, 104: 898–906.

    Article  Google Scholar 

  6. Bazer, J. and Burridge, R., Energy partition in the reflection and refraction of plane waves. SIAM Journal of Applied Mathematics, 1978, 34: 78–92.

    Article  MathSciNet  Google Scholar 

  7. Wang, C.H. and Rose, L.R.F., Wave reflection and transmission in beams containing delamination and in-homogeneity. Journal of Sound and Vibration, 2003, 264: 851–872.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China

    Li Zhou & Wanchun Yuan

Authors
  1. Li Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wanchun Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 50478037 and 10572058) and the Research Foundation for the Doctoral Program of Higher Education (No. 20050287016).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhou, L., Yuan, W. Power Reflection and Transmission in Beam Structures Containing a Semi-Infinite Crack. Acta Mech. Solida Sin. 21, 177–188 (2008). https://doi.org/10.1007/s10338-008-0821-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-008-0821-6

Key words

Search

Navigation