Abstract
Major obstacles to formulating a simple retention mechanism for reversed-phase liquid chromatography are identified as the heterogeneous composition of the stationary phase, the difficulty of providing a working definition for the phase ratio, and uncertainty as to whether the distribution mechanism for varied compounds are a partition or adsorption process or some combination of both. Some insight into the retention mechanism is provided by isotherm measurements, studies of surface excess adsorption, and molecular dynamics simulations, while on the other hand, retention factor measurements offer little guidance as they represent an average of various and variable contributing factors that can only be deconvoluted by assuming a specific model. The interphase model offers a phenomenological description of the active region of the stationary phase responsible for retention, but is not connected with any specific mathematical formulation on the retention mechanism. Mechanistic models based on solvophobic theory, lattice theories, and partition displacement models are of limited practical utility because of their complexity and unrealistic assumptions required in most part to simplify the mathematical description of the interphase region. Linear free energy relationships, such as the solvation parameter model, provide a simpler solution offering useful insights into the retention process for column selection and mobile phase optimization. Even here, caution is indicated as the interpretation of solvent effects on system constants implies an understanding of the retention mechanism which remains an enigma in search of a solution.

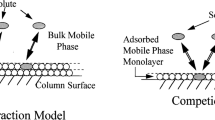
Reproduced from [92] with permission

Reproduced from [92] with permission




Similar content being viewed by others
References
Poole CF (2003) The essence of chromatography. Elsevier, Amsterdam
Fanali S, Haddad PR, Poole CF, Riekkola M-L (eds) (2017) Liquid chromatography, vol 1, 2, 2nd edn. Elsevier, Amsterdam
Snyder LR, Kirkland JJ, Glajch (1997) Practical HPLC method development, 2nd edn.Wiley-Interscience, New York
Roses M, Subirats X, Bosch E (2008) Retention models for ionizable compounds in reversed-phase liquid chromatography. Effect of variation of mobile phase composition and temperature. J Chromatogr A 1216:1756–1775
Vailaya A, Horvath C (1998) Retention in reversed-phase liquid chromatography: partition or adsorption. J Chromatogr A 829:1–37
Tan LC, Carr PW (1997) Revisionist look at solvophobic driving forces in reversed-phase liquid chromatography—2. Partitioning vs. adsorption mechanism in monomeric alkyl bonded phase supports. J Chromatogr A 775:1–12
Wang M, Mallette J, Parcher JF (2008) Fundamental mathematical relationships for retention volumes in liquid chromatography. J Chromatogr A 1213:105–109
Poole CF, Poole SK (2009) Foundations of retention in partition chromatography. J Chromatogr A 1216:1530–1550
Rimmer CA, Simmons CR, Dorsey JG (2002) The measurement and meaning of the void volume in reversed-phase liquid chromatography. J Chromatogr A 965:219–232
Moldoveau S, Victor D (2015) Estimation of the phase ratio in reversed-phase high-performance liquid chromatography. J Chromatogr A 1381:194–201
Gritti F, Kazakevich Y, Guiochon G (2007) Measurement of hold-up volumes in reversed-phase liquid chromatography—definition and comparison between static and dynamic methods. J Chromatogr A 1161:157–169
Wang M, Mallette J, Parcher JF (2011) Comparison of void volume, mobile phase volume and accessible volume determined from retention data for oligomers in reversed-phase liquid chromatography systems. J Chromatogr A 1218:2995–3001
Tsopslas F, Petropoulou O, Tsantili-Kakouliolou A (2010) Void volume markers in reversed-phase and biomimetic liquid chromatography J Chromatogr A 1217:2847–2854
Giaquinto A, Liu ZX, Bach A, Kazakevich Y (2009) Surface area of reversed-phase HPLC. columns Anal Chem 80:6358–6364
Vajda P, Bocian S, Buszweski B, Felinger A (2010) Examination of surface heterogeneity of reversed-phase materials with solvent adsorption. J Sep Sci 33:3644–3654
Gritti F, Guiochon G (2006) Heterogeneity of the adsorption mechanism of low molecular weight compounds in reversed-phase liquid chromatography. Anal Chem 78:5823–5834
Gritti F, Guiochon G (2005) Critical contribution of nonlinear chromatography to the understanding of the retention mechanism in reversed-phase liquid chromatography. J Chromatogr A 1099:1–42
Rafferty JL, Zhang L, Siepmann JI. Schure MR (2007) Retention mechanism in reversed-phase liquid chromatography. A Mol Simul Anal Chem 79:6551–6558
Lindsey RK, Rafferty JL, Eggimann BL, Siepmann JL, Schure MR (2013) Molecular simulation studies of reversed-phase liquid chromatography. J Chromatogr A 1287:60–82
El-Hage K, Gupta PK, Bemish R, Meuwly M (2017) Molecular mechanisms underlying solute retention at heterogeneous interfaces. J Phys Chem Lett 8:4600–4607
Rafferty JL, Siepmann JL, Schure MR (2011) Retention mechanism of polycyclic aromatic hydrocarbons in reversed-phase liquid chromatography with monomeric stationary phases. J Chromatogr A 1218:9183–9193
Klatte SJ, Beck TL (1996) Microscopic simulations of solute transfer in reversed-phase liquid chromatography. J Phys Chem 100:5931–5934
Rafferty JL, Siepmann JL, Schure MR (2012) A molecular simulation study of the effects of stationary phase and solute chain length in reversed-phase liquid chromatography. J Chromatogr A 1223:24–34
Guillaume YC, Guinchard C (1998) Participation of cluster species in the solvation mechanism of a weak polar solute in a methanol-water mixture over a 0.2–0.7 water fraction range: High-performance liquid chromatography study. Anal Chem 70:608–615
Marcus Y (2012) The structure of and interactions in binary acetonitrile + water mixtures. J Phys Org Chem 25:1072–1082
Alvarezzepeda A, Garman BN, Martire DE (1992) Thermodynamic study of the marked differences between acetonitrile water and methanol water mobile phase systems in reversed-phase liquid chromatography. Anal Chem 64:1978–1984
Kazakevich YV, LoBrutto R, Chan P (2001) Interpretation of the excess adsorption isotherms on the surface of reversed-phase adsorbents—effect on the analyte retention. J Chromatogr A 913:75–87
Gritty F, Kazakevich YV, Guiochon G (2007) Effect of the surface coverage of endcapped C-18 silica on the excess adsorption isotherms of commonly used organic solvents from water in reversed-phase liquid chromatography. J Chromatogr A 1169:111–124
Bocian S, Vajda P, Felinger A, Buszewski B (2008) Solvent excess adsorption on the stationary phases for reversed-phase liquid chromatography with polar functional groups. J Chromatogr A 1204:35–41
Buntz S, Figus M, Liu Z, Kazakevich YV (2012) Excess adsorption of binary aqueous organic mixtures on various reversed-phase packing materials. J Chromatogr A 1240:104–112
Vajda P, Felinger A, Guiochon G (2013) Evaluation of surface excess isotherms in liquid chromatography. J Chromatogr A 1291:41–47
Bocian S, Skrinjar T, Bolanca T, Buszewski B (2017) How high pressure unifies solvation processes in liquid chromatography. JOAC Int 100:1647–1651
McCormick RM, Karger BL (1980) Role of organic modifier sorption on retention phenomena in reversed-phase liquid chromatography. J Chromatogr 199:259–273
McCormick RM, Karger BL (1980) Distribution of mobile phase components and determination of dead volume in reversed-phase liquid chromatography. Anal Chem 52:2249–2257
Rafferty JL, Siepmann JL, Schure MR (2011) Mobile phase effects in reversed-phase liquid chromatography. A comparison of acetonitrile/water and methanol/water solvents as studied by molecular simulation. J Chromatogr A 1218:2203–2213
Poole CF (2015) An interphase model for retention in liquid chromatography. J Planar Chromatogr 28:98–105
Rafferty JL, Siepmann JL, Schure MR (2009) The effects of chain length, polar embedded functional groups, pressure and pore shape on structure and retention in reversed-phase liquid chromatography. Molecular level insights from Monte Carlo simulations. J Chromatogr A 1216:2320–2331
Klatte SJ, Beck TL (1995) Molecular dynamics simulations of tethered alkane chromatographic stationary phases. J Phys Chem 43:16024–16032
Neue UD, O’Gara JE, Mandez A (2006) Selectivity in reversed-phase separations— influence of the stationary phase. J Chromatogr A 1127:161–174
Vajda P, Bocian S, Buzewski B, Felinger A (2012) Effect of polar interactions on the nonlinear behavior of phenol and aniline in reversed-phase liquid chromatography. J Chromatogr A 1228:155–164
Gritti F, Guiochon G (2009) Characteristics of the adsorption mechanism of acidic-basic compounds with two pK(a) in reversed-phase liquid chromatography. J Chromatogr A 1216:6917–6930
Wang C, Guo Z, Long Z, Zhang X, Liang X (2013) Overloading study of basic compounds with positively charged C18 column in liquid chromatography. J Chromatogr A 1281:60–66
McDonald PD (2003) Improving our understanding of reversed phase separations for the 21 st century. Adv Chromatogr 42:323–375
Kazakevich YV (2006) High-performance liquid chromatographic retention mechanisms and their mathematical description J Chromatogr A 1126:232–243
Nikitas P, Pappa-Louisi A, Agrafiotou (2002) Effect of the organic modifier concentrations on the retention in reversed-phase liquid chromatography 1. General semi-thermodynamic treatment for adsorption and partition mechanisms. J Chromatogr A 946:9–32
Jaroniec M (1993) Partition and displacement models in reversed-phase liquid chromatography with mixed eluents. J Chromatogr A 656:37–50
Tijssen R, Schoemekers PJ, Bohmer MR, Koopal LK, Billiet HAH (1993) Lattice models for the description of partitioning adsorption and retention in reversed-phase liquid chromatography including surface and shape effects. J Chromatogr A 656:135–196
Vailaya A, Horvath C (1997) Solvophobic theory and normalized free energies of nonpolar substances in reversed-phase chromatography. J Phys Chem 101:5875–5888
Vailaya A (2005) Fundamentals of reversed-phase chromatography. Thermodynamic and exothermodynamic treatment. J Liq Chromatogr Rel Technol 28:965–1054
Boehm RE, Martire DE (1985) Unified theory of retention and selectivity in liquid chromatography 2. Reversed-phase liquid chromatography with chemically bonded phases. J Phys Chem 87:1045–1062
Boehm RE, Martire DE (1994) Theory of liquid chromatographic retention and solute transfer thermodynamics using the Bethe-Guggenheim quasi-chemical approach. J Phys Chem 98:1317–1327
Dill KA (1987) The mechanism of solute retention in reversed-phase liquid chromatography. J Phys Chem 91:1980–1988
Dorsey JG, Dill KA (1989) The molecular mechanism of retention in reversed-phase liquid chromatography. Chem Rev 89:331–346
Poplewska I, Antos D (2005) Effect of adsorption of organic solvent on the band profiles in reversed-phase non-linear chromatography. Chem Eng Sci 60:1411–1427
Jouyban A, Soltani S, Shayanfar A, Pappa-Louisi A (2011) Modeling the effects of type and concentration of organic modifiers, column type and chemical structure of analytes on the retention in reversed-phase liquid chromatography using a single model. J Chromatogr A 1218:6454–6463
Borowko M, Oscik-mendyk B, Borowko P (2005) Theory of retention in reversed-phase liquid chromatography with ternary mobile phases. J Phys Chem B 44:21056–21062
Kwiemiewski I, Rycyk M (2017) The use of Oscik’s equation to describe the retention in reversed-phase liquid chromatography. J Chromatogr A 1496:45–50
Nikitas P, Pappa-Louisi A, Agrafiotou P (2002) Affect of the organic modifier on retention in reversed-phase liquid chromatography. II tests using various simplified models. J Chromatogr A 946:33–45
Put R, vander Heyden Y (2007) Review on modeling aspects on reversed-phase liquid chromatographic quantitative structure retention relationships. Anal Chim Acta 602:164–172
Poole CF, Poole SK (2002) Column selectivity from the perspective of the solvation parameter model. J Chromatogr A 965:263–299
Vitha MH, Carr PW (2006) The chemical interpretation and practice of linear solvation energy relationships in chromatography. J Chromatogr A 1126:143–194
Poole CF, Lenca N (2017) Applications of the solvation parameter model in reversed-phase liquid chromatography. J Chromatogr A 1486:2–19
Snyder LR, Dolan JW, Carr PW (2004) The hydrophobic-subtraction model of reversed-phase column selectivity. J Chromatogr A 1060:77–116
Snyder LR, Dolan JW, Marchand DA, Carr PW (2012) The hydrophobic-substraction model of reversed-phase column selectivity. Adv Chromatogr 50:297–376
Abraham MH (1993) Scales of solute hydrogen bonding. Their construction and application to physicochemical and biochemical processes. Chem Soc Chem Rev 221:73–83
Abraham MH, Ibrahim A, Zissmos AM (2004) Determination of sets of solute descriptors from chromatographic measurements. J Chromatogr A 1037:29–47
Poole CF, Atapattu SN, Poole SK, Bell AN (2009) Determination of solute descriptors by chromatographic methods. Anal Chim Acta 652:32–53
Poole CF, Ariyasena TC, Lenca N (2013) Estimation of the environmental properties of compounds from chromatographic measurements and the solvation parameter model. J Chromatogr A 1317:85–104
Zissimos AM, Abraham MH, Du CM, Valko K, Bevan C, Reynolds D, Wood J, Tam KY (2002) Calculation of Abraham descriptors from experimental data from seven HPLC systems: evaluation of five different methods of calculation. J Chem Soc Perkin Trans 2:2001–2010
Tulp HC, Goss K-U, Schwarzenbach RP, Fenner K (2008) Experimental determination of LSER parameters for a set of 78 diverse pesticides and pharmaceuticals. Environ Sci Technol 47:2034–2040
Andries JPM, Claessens HA, vander Heyden Y, Buydens LMC (2009) Strategy for reduced calibration sets to develop quantitative structure-retention relationships in high-performance liquid chromatography. Acta Chim Acta 652:180–188
Sandi A, Nagy N, Szepesy L (2000) Characterization of reversed-phase columns using linear free energy relationships III. Effect of the organic modifier and the mobile phase composition. J Chromatogr A 893:215–234
Szepesy L (2002) Effect of molecular interactions on retention and selectivity in reversed-phase liquid chromatography. J Chromatogr A 960:69–83
Vonk EC, Lewandowska K, Claessens HA, Kaliszan K, Cramers CA (2003) Quantitative structure-retention relationships in reversed-phase liquid chromatography using several stationary and mobile phases. J Sep Sci 26:777–792
Gotta J, Keunchkarian S, Castells C, Reta M (2012) Predicting retention in reversed-phase liquid chromatography at different mobile phase compositions and temperature using the solvation parameter model. J Sep Sci 35:2699–2709
Poole CF (2005) Models for the adsorption of organic compounds at gas-water interfaces. J Environ Monit 7:577–580
Atapattu SN, Poole CF (2009) Models for the sorption of volatile organic compounds by diesel soot and atmospheric aerosols. J Environ Monit 11:815–822
Lepont C, Gunatillaka AD, Poole CF (2001) Retention characteristics of porous graphitic carbon in reversed-phase liquid chromatography with methanol-water mobile phases. Analyst 129:1318–1325
Kiridena W, Poole CF (1998) Influence of solute size and site-specific surface interactions on the prediction of retention in liquid chromatography using the solvation parameter model. Analyst 123:1265–1270
Wu D, Lucy CA (2017) Linear solvation energy relationships in normal-phase chromatography based on gradient separations. J Chromatogr A 1516:64–70
Poole SK, Kollie TO, Poole CF (1994) The Influence of temperature on the mechanism by which compounds are retained in gas–liquid Chromatography. J Chromatogr 664:229–251
Abraham MH, Poole CF, Poole SK (1999) Classification of stationary phases and other materials by gas chromatography. J Chromatogr A 842:79–114
Ronco NR, Monestrina F, Romero LM, Castells CB (2017) Determination of gas–liquid partition coefficients of several organic solutes in trihexyl(tetradecyl)phosphonium bromide using capillary gas chromatography columns. J Chromatogr A 1501:134–141
Li Q, Poole CF (2000) Influence of interfacial adsorption on the system constants of the solvation parameter model in gas-liquid chromatography. Chromatographia 52:639–647
Chu Y, Poole CF (2003) System maps for retention of neutral organic compounds under isocratic conditions on a reversed-phase monolithic column. J Chromatogr A 1001:113–121
Kiridena W, Atapattu SN, Poole CF, Koziol WW (2008) System maps for reversed-phase liquid chromatography on an octadecylsiloxane-bonded silica stationary phase (SunFire C18). Chromatographia 68:11–17
Kiridena W, Poole CF (1998) Structure-driven retention model for optimization of ternary solvent systems in reversed-phase liquid chromatography. Chromatographia 48:607–614
Bolliet D, Poole CF (1998) Mixture-design approach to retention prediction using the solvation parameter model and ternary solvent systems in reversed-phase liquid chromatography. Anal Commun 35:253–256
Coym JW (2010) Evaluation of ternary mobile phases for reversed-phase liquid chromatography. Effect of composition on retention mechanism. J Chromatogr A 1217:5957–5964
Kiridena W, Poole CF, Koziol WW (2003) Reversed-phase chromatography on a polar endcapped octadecylsiloxane-bonded silica stationary phase with water as the mobile phase. Chromatographia 57:703–708
Kiridena W, Poole CF, Koziol WW (2004) Effect of solvent strength and temperature on retention for a polar-endcapped, octadecylsiloxane-bonded silica stationary phase with methanol-water mobile phases. J Chromatogr A 1060:177–185
Atapattu SN, Poole CF, Praseuth MB (2017) System maps for retention of small neutral compounds on superficially porous ethyl-bridged, octadecylsiloxane-bonded silica stationary phase in reversed-phase liquid chromatography. Chromatographia 80:1279–1286
Atapattu SN, Poole CF (2010) Factors affecting the interpretation of selectivity on synergi reversed-phase columns. Chromatographia 71:185–193
Kiridena W, DeKay C, Villiere ND, Koziol WW, Poole CF (2005) System maps for XTerra MS C18: effect of solvent type on selectivity in reversed-phase liquid chromatography. Chromatographia 61:587–593
Poole CF, Ahmed H, Kiridena C, DeKay C, Koziol WW (2005) Contribution of steric repulsion to retention on an octadecylsiloxane-bonded silica stationary phase in reversed-phase liquid chromatography. Chromatographia 62:553–561
Kiridena W, DeKay C, Koziol WW, Ali Z, Ahmed H, Poole CF (2006) Insights into the retention mechanism on a pentafluorophenylpropylsiloxane-bonded silica stationary phase (Discovery HS F5) in RP-LC. Chromatographia 63:407–417
Poole CF, Ahmed H, Kiridena W, DeKay C, Koziol WW (2007) Insights into the retention mechanism on perfluorohexylpropylsiloxane-bonded (Fluophase RP) and octadecylsiloxane-bonded (Betasil C18) stationary phases based on the same silica substrate in RP-LC. Chromatographia 65:127–139
Poole CF, Kiridena W, DeKay C, Koziol WW, Rosencrans RD (2006) Insights into the retention mechanism on an octadecylsiloxane-bonded silica stationary phase (HyPURITY C18) in reversed-phase liquid chromatography. J Chromatogr A 1115:133–141
Atapattu SN, Poole CF, Praseuth MB (2016) System maps for retention of small neutral compounds on a superficially porous particle column in reversed-phase liquid chromatography. J Chromatogr A1468:250–256
Atapattu SN, Poole CF, Praseuth MB (2018) Insights into the retention mechanism of small neutral compounds on octylsiloxane-bonded and diisobutyloctadecylsiloxane-bonded silica stationary phases in reversed-phase liquid chromatography. Chromatographia 81:373–385
Kiridena W, Poole CF, Atapattu SN, Qian J, Koziol WW (2007) Comparison of the separation characteristics of the organic-inorganic hybrid octadecyl stationary phases Xterra MS C18 and XBridge C18 and Shield RP18 in reversed-phase liquid chromatography. Chromatographia 67:453–460
Kiridena W, Atapattu SN, Poole CF, Koziol WW (2008) Comparison of the separation characteristics of the organic-inorganic hybrid stationary phases XBridge C8 and phenyl and XTerra phenyl in reversed-phase liquid chromatography. Chromatographia 68:491–500
Abraham MH, Roses M, Poole CF, Poole SK (1997) The characterization of reversed-phase high performance liquid chromatographic C-18 stationary phases. J Phys Org Chem 10:358–368
Poole CF, Poole SK, Gunatilleka AD (2000) In search of a chromatographic model for biopartitioning. Adv Chromatogr 40:159–230
Wang A, Carr PW (2002) Comparative study of linear solvation energy relationship, linear solvent strength theory, and typical conditions model for retention prediction in reversed-phase liquid chromatography. J Chromatogr A 965:3–23
Walter TH, ireneta P, Capparella P (2005) Mechanism of retention loss when C8 and C18 HPLC columns are used with highly aqueous mobile phases. J Chromatogr A 1075:177–183
Carr PW, Dolan JW, Neue UD, Snyder LR (2011) Contributions to reversed-phase column selectivity. I Steric interactions. J Chromatogr A 1218:1724–1749
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Human rights and participants
This article does not contain any studies with human participants or animals performed by the author.
Additional information
Published in Chromatographia’s 50th Anniversary Commemorative Issue.
Rights and permissions
About this article
Cite this article
Poole, C.F. Influence of Solvent Effects on Retention of Small Molecules in Reversed-Phase Liquid Chromatography. Chromatographia 82, 49–64 (2019). https://doi.org/10.1007/s10337-018-3531-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10337-018-3531-3