Evaluating release alternatives for a long-lived bird species under uncertainty about long-term demographic rates

Abstract

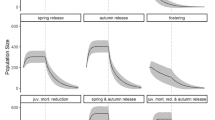
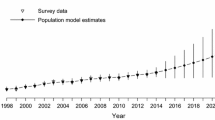
The release of animals to reestablish an extirpated population is a decision problem that is often attended by considerable uncertainty about the probability of success. Annual releases of captive-reared juvenile Whooping Cranes (Grus americana) were begun in 1993 in central Florida, USA, to establish a breeding, non-migratory population. Over a 12-year period, 286 birds were released, but by 2004, the introduced flock had produced only four wild-fledged birds. Consequently, releases were halted over managers’ concerns about the performance of the released flock and uncertainty about the efficacy of further releases. We used data on marked, released birds to develop predictive models for addressing whether releases should be resumed, and if so, under what schedule. To examine the outcome of different release scenarios, we simulated the survival and productivity of individual female birds under a baseline model that recognized age and breeding-class structure and which incorporated empirically estimated stochastic elements. As data on wild-fledged birds from captive-reared parents were sparse, a key uncertainty that confronts release decision-making is whether captive-reared birds and their offspring share the same vital rates. Therefore, we used data on the only population of wild Whooping Cranes in existence to construct two alternatives to the baseline model. The probability of population persistence was highly sensitive to the choice of these three models. Under the baseline model, extirpation of the population was nearly certain under any scenario of resumed releases. In contrast, the model based on estimates from wild birds projected a high probability of persistence under any release scenario, including cessation of releases. Therefore, belief in either of these models suggests that further releases are an ineffective use of resources. In the third model, which simulated a population Allee effect, population persistence was sensitive to the release decision: high persistence probability was achieved only through the release of more birds, whereas extirpation was highly probable with cessation of releases. Despite substantial investment of time and effort in the release program, evidence collected to date does not favor one model over another; therefore, any decision about further releases must be made under considerable biological uncertainty. However, given an assignment of credibility weight to each model, a best, informed decision about releases can be made under uncertainty. Furthermore, if managers can periodically revisit the release decision and collect monitoring data to further inform the models, then managers have a basis for confronting uncertainty and adaptively managing releases through time.

Appendix

The statistical estimation models for survival and breeding class transition are described in the text. The accompanying mathematical descriptions are provided below and are more fully developed in Moore et al. (in preparation). Estimates from the models (Table 3) were used to construct the baseline PVA model.

Survival estimation

Each female bird j released into the wild as part of cohort c was a member of age or breeding class k (k ∈ {0, 1, 2, 3, 4 + , P, N, F}) in period i (3-month divisions of the year, starting from January 1993). The number of days that bird j survived within period i was assumed to be binomially distributed with probability ${ \text{p}_{ij}}(k,c)^{{1/d}_{i}}$ over x _ij exposure days, where period i is d _i days in length and 0 ≤ x _ij ≤ d _i.

Quarterly survival probability was modeled as a linear function of a mean (an intercept plus a female fixed effect) and random effects of age/breeding class, time, cohort, and individual:

$$ \begin{aligned}\log\!{\text{it}}\left({p_{ij} \left({k,c} \right)} \right)& = {{\upalpha}}_{k}^{G} + {{\updelta}}_{i}^{T} + {{\updelta}}_{cj}^{*} \\ & = \left({{{\upmu}}_{\text{female}} + {{\updelta}}_{k}^{G}} \right) + {{\updelta}}_{i}^{T} + \left({{{\updelta}}_{c}^{C0} + {{\updelta}}_{j}^{B0}} \right)I\left({\text{age = 0}} \right) \\ & + \left({{{\updelta}}_{c}^{C1} + {{\updelta}}_{j}^{B1}} \right)I\left({\text{age = 1}} \right) \\& + \left({{{\updelta}}_{c}^{{{\text{C}}2 +}} + {{\updelta}}_{j}^{{{\text{B}}2 +}}} \right)I\left({{\text{age}} \ge 2} \right)\\ \end{aligned} $$

where δ ^G_k is a random effect due to membership in age or breeding class k, δ ^T_i is a random effect due to period i, δ ^C*_c are age-class specific random effects due to membership in release cohort c, δ ^B*_j are age-class specific random effects due to bird j, and I(z) is the indicator function for expression z. Random effects were modeled as deviates from zero-centered normal distributions with corresponding variance parameters σ ²_G , σ ²_T , σ ²_C0 , σ ²_C1 , σ ²_C2+ , σ ²_B0 , σ ²_B1 , and σ ²_B2+ .

Posterior distributions of annual age and breeding-class specific survival rates (φ_k) were estimated by summing appropriate terms of the model above, transforming the sum to the probability scale, and multiplying four of the resulting terms together:

$$ {\varphi_{\it k}}= \prod\limits_{i = 1}^{4} {\log\!{\text{it}}^{- 1} \left({{{\upalpha}}_{k}^{G} + {{\updelta}}_{i}^{T} + {{\updelta}}_{cj}^{*}} \right)} .$$

Estimation of productivity and breeding class transition probabilities

Transition into breeding class P occurred when a female bird of age ≥2 years first exhibited pairing behavior. For never-paired bird j that was age k (k = 1, 2, 3, 4+) in the year previous to i, we assumed that first pairing occurred as a Bernoulli outcome with probability θ ^UP_ij (k). Transition probability was thus modeled as a linear function of fixed intercept (μ_UP) and age-specific (β_k) effects and of random effects of time (δ ^PT_i ) and bird (δ ^PB_j ):

$$ \log\!{\text{it}}\left({{{\uptheta}}_{ij}^{UP} \left(k \right)} \right) = {{\upmu}}_{UP} + {{\upbeta}}_{k} + {{\updelta}}_{i}^{PT} + {{\updelta}}_{j}^{PB} $$

Random effects were modeled as deviates from zero-centered normal distributions with corresponding variance parameters σ ²_PT and σ ²_PB . We obtained posterior distributions of annual age-specific transition probability into class P (ψ ^(k)_UP ) by transformation of the above sum.

Transition from class P into class N occurred when a female produced her first nestling but failed to produce a fledgling. Transition from class P into class F occurred when a female’s first nestling developed into a fledgling (male or female). For bird j belonging to class P, both events were assumed to occur as Bernoulli outcomes with probabilities θ ^PN_j and θ ^PF_j , respectively. Linear models relating each transition probability to a fixed intercept and a random effect due to bird were:

$$ \log\!{\text{it}}\left({{{\uptheta}}_{j}^{PN}} \right) = {{\upmu}}_{PN} + {{\updelta}}_{j}^{PNB} \quad{\text{and}}\quad\log\!{\text{it}}\left({{{\uptheta}}_{j}^{PF}} \right) = {{\upmu}}_{PF} + {{\updelta}}_{j}^{PFB} $$

Random effects were modeled as deviates from zero-centered normal distributions with corresponding variance parameters σ ²_PNB and σ ²_PFB . We obtained posterior distributions of annual transition probability from class P into classes N (ψ_PN) or F (ψ_PF). As no Florida bird has ever produced more than one fledgling in a year, ψ_PF serves as the estimate of productivity for birds in class P.

Transition from class N into class F occurred when a female who had only ever produced a nestling in prior attempts produced her first fledgling (male or female). We assumed that this event was a Bernoulli outcome with probability ψ_NF. Similarly, a bird already in class F produces another fledgling with probability ψ_FF. We modeled each of these probabilities as a simple mean with no random effects:

$$ \log\!{\text{it}}\left({{{\uppsi}}_{NF}} \right) = {{\upmu}}_{NF}\quad{\text{and}}\quad\log\!{\text{it}}\left({{{\uppsi}}_{FF}} \right) = {{\upmu}}_{FF} $$

These probabilities effectively serve as estimates of productivity for birds in class N and F, respectively.

Table 3 Estimates of age and breeding-class specific mean annual survival rate (φ_i), mean breeding transition rate (ψ_ij), and associated random effects (σ_i) of 286 captive-reared female Whooping Cranes reintroduced in Florida, USA, 1993–2004 (Moore et al. in preparation)