Abstract
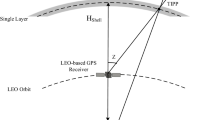
The ionospheric shell height has an impact on the estimated differential code bias (DCB) and total electron content (TEC) obtained by global navigation satellite system (GNSS) data, especially for a single site. However, the shell height is generally considered as a fixed value. Based on data from the international GNSS service (IGS), we propose the concept of optimal ionospheric shell height, which minimizes |ΔDCB| when compared to the DCB provided by Center for Orbit Determination in Europe (CODE). Based on the data from five IGS stations at high, middle, and low latitudes during the time 2003–2013, we investigate the variation in the optimal ionospheric shell height and its relation with the solar activity. Results indicate that the relation between the mean of the optimal ionospheric shell height and the latitude is N-shaped. At the three stations at midlatitude, the mean value almost increases linearly with the latitude. The optimal ionospheric shell heights show 11-year and 1-year periods. The influences of the solar activity are related to the means of the optimal ionospheric shell height during the time 2003–2013. The slope of the linear fitting decreases with the mean value. Using the data from 2003 to 2013, we estimate the daily optimal ionospheric shell heights for 2014 by using the Fourier fitting method and then calculate the daily average of ΔDCB of the observed satellites by comparing to CODE results. The statistical results of the daily average in 2014 show that the optimal ionospheric shell height is much better than the fixed one. From the high-latitude station to the low-latitude station, the improvements in the mean value are about 75, 92, 96, 50, and 88% and the root-mean-squares are reduced by about 0.16, 2.09, 2.01, 1.01, and 0.02 TECu, respectively.







Similar content being viewed by others
References
Alizadeh MM, Schuh H, Todorova S, Schmidt M (2011) Global ionosphere maps of VTEC from GNSS, satellite altimetry, and Formosat-3/COSMIC data. J Geod 85(12):975–987
Anghel A, Carrano C, Komjathy A, Astilean A, Leita T (2009) Kalman filter-based algorithms for monitoring the ionosphere and plasmasphere with GPS in near real-time. J Atmos Sol Terr Phys 71(1):158–174
Arikan F, Nayir H, Sezen U, Arikan O (2008) Estimation of single station interfrequency receiver bias using GPS-TEC. Radio Sci 43(4):RS4004. https://doi.org/10.1029/2007RS003785
Birch MJ, Hargreaves JK, Bailey GJ (2002) On the use of an effective ionospheric height in electron content measurement by GPS reception. Radio Sci 37(1):1015. https://doi.org/10.1029/2000RS002601
Brunini C, Camilion E, Azpilicueta F (2011) Simulation study of the influence of the ionospheric layer height in the thin layer ionospheric model. J Geod 85(9):637–645
Carrano C, Anghel A, Quinn R, Groves K (2009) Kalman filter estimation of plasmaspheric total electron content using GPS. Radio Sci 44(1):RS0A10. https://doi.org/10.1029/2008RS004070
Chen P, Yao Y, Yao W (2017) Global ionosphere maps based on GNSS, satellite altimetry, radio occultation and DORIS. GPS Solut 21(2):639–650
Ciraolo L, Azpilicueta F, Brunini C, Meza A, Radicela SM (2007) Calibration errors on experimental slant total electron content determined with GPS. J Geod 81(2):111–120. https://doi.org/10.1007/s00190-006-0093-1
Coco DS, Coker C, Dahlke SR, Clynch JR (1991) Variability of GPS satellite differential group delay biases. IEEE Tran Aerosp Electron Syst 27(6):931–938. https://doi.org/10.1109/7.104264
Coster A, Williams J, Weatherwax A, Rideout W, Herne D (2013) Accuracy of GPS total electron content: GPS receiver bias temperature dependence. Radio Sci 48(2):190–196. https://doi.org/10.1002/rds.20011
Davies K (1990) Ionospheric radio. Peter Peregrinus Ltd, London, pp 70–73
Dyrud L, Jovancevic A, Brown A, Wilson D, Ganguly S (2008) Ionospheric measurement with GPS: receiver techniques and methods. Radio Sci 43(6):RS6002. https://doi.org/10.1029/2007rs003770
Horvath I, Crozier S (2007) Software developed for obtaining GPS-derived total electron content values. Radio Sci 42(2):RS2002
Huang Z, Yuan H (2014) Ionospheric single-station TEC short-term forecast using RBF neural network. Radio Sci 49(4):283–292
Iijima BA, Harris IL, Ho CM, Lindqwister UJ, Mannucci AJ, Pi X, Reyes MJ, Sparks LC, Wilson BD (1999) Automated daily process for global ionospheric total electron content maps and satellite ocean ionospheric calibration based on Global Positioning System. J Atmos Solar Terr Phys 61(16):1205–1218
Kao S, Tu Y, Chen W, Weng D, Ji S (2013) Factors affecting the estimation of GPS receiver instrumental bias. Surv Rev 45(328):59–67
Komjathy A, Langley RB (1996) The effect of shell height on high precision ionospheric modelling using GPS. In: Proceedings of the international GPS service for geodynamics (IGS) workshop in Silver Spring, MD, 19–21 March 1996, pp 193–203
Lanyi GE, Roth T (1988) A comparison of mapped and measured total ionospheric electron content using Global Positioning System and beacon satellite observations. Radio Sci 23(4):483–492
Li Z, Yuan Y, Li H, Ou J, Huo X (2012) Two-step method for the determination of the differential code biases of COMPASS satellites. J Geod 86(11):1059–1076. https://doi.org/10.1007/s00190-012-0565-4
Li M, Yuan Y, Wang N, Li Z, Li Y, Huo X (2017a) Estimation and analysis of Galileo differential code biases. J Geod 91(3):279–293
Li M, Yuan Y, Zhang B, Wang N, Li Z, Liu X, Zhang X (2017b) Determination of the optimized single-layer ionospheric height for electron content measurements over China. J Geod. https://doi.org/10.1007/s00190-017-1054-6
Lomb NR (1976) Least-squares frequency analysis of unequally spaced data. Astrophys Space Sci 39(2):447–462
Lu W, Ma G, Wang X, Wan Q, Li J (2017) Evaluation of ionospheric height assumption for single station GPS-TEC derivation. Adv Space Res 60(2):286–294
Ma G, Maruyama T (2003) Derivation of TEC and estimation of instrumental biases from GEONET in Japan. Ann Geophys 21(10):2083–2093
Ma XF, Maruyama T, Ma G, Takeda T (2005) Determination of GPS receiver differential biases by neural network parameter estimation method. Radio Sci 40(1):RS1002. https://doi.org/10.1029/2004RS003072
Mannucci AJ, Wilson BD, Yuan DN, Ho CH, Lindqwister UJ, Runge TF (1998) A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci 33(3):565–583
Niranjan K, Srivani B, Gopikrishna B, Rama Rao PVS (2007) Spatial distribution of ionization in the equatorial and low-latitude ionosphere of the Indian sector and its effect on the pierce point altitude for GPS applications during low solar activity periods. J Geophys Res. https://doi.org/10.1029/2006JA011989
Rao PVS, Niranjan K (2006) Prasad DSVVD, Krishna SG, Uma G (2006) On the validity of the ionospheric pierce point (IPP) altitude of 350 km in the Indian equatorial and low-latitude sector. Ann Geophys 24(8):2159–2168
Sardón E, Zarraoa N (1997) Estimation of total electron content using GPS data: how stable are the differential satellite and receiver instrumental biases? Radio Sci 32(5):1899–1910. https://doi.org/10.1029/97RS01457
Sardón E, Rius A, Zarraoa N (1994) Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from global positioning system observations. Radio Sci 29(3):577–586
Scargle JD (1982) Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data. Astrophys J 263:835–853
Schaer S, Beutler G, Mervart L, Rothacher M, Wild U (1995) Global and regional ionosphere models using the GPS double difference phase observable. In: Proceedings of the IGS workshop on special topics and new directions, Potsdam, Germany, May 15–17, pp 77–92
Sekido M, Kondo T, Kawai E, Imae M (2003) Evaluation of GPS-based Ionospheric TEC Map by Comparing with VLBI Data. Radio Sci 38(4):1069. https://doi.org/10.1029/2000RS002620
Shukla AK, Das S, Nagori N, Sivaraman MR, Bandyopadhyay K (2009) Two-shell ionospheric model for Indian region: a novel approach. IEEE Trans Geosci Remote Sens 47(8):2407–2412
Wang N, Yuan Y, Li Z, Montenbruck O, Tan B (2016) Determination of differential code biases with multi-GNSS observations. J Geod 90(3):209–228
Warnant R (1997) Reliability of the TEC computed using GPS measurements—the problem of hardware biases. Acta Geod Geophys Hung 32(3–4):451–459. https://doi.org/10.1007/BF03325514
Yuan Y, Ou J (2002) Differential areas for differential stations (DADS): a new method of establishing grid ionospheric model. Chin Sci Bull 47(12):1033–1036. https://doi.org/10.1007/BF02907577
Yuan YB, Ou JK (2004) A generalized trigonometric series function model for determining ionospheric delay. Prog Nat Sci 14(11):1010–1014
Acknowledgements
This study is based on data services provided by the IGS (International GNSS Service) and CODE (the Center for Orbit Determination in Europe). This work is supported by the National Natural Science Foundation of China (NSFC Grant 41574146 and 41774162).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhao, J., Zhou, C. On the optimal height of ionospheric shell for single-site TEC estimation. GPS Solut 22, 48 (2018). https://doi.org/10.1007/s10291-018-0715-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-018-0715-0