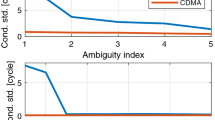
Abstract
GLONASS ambiguity resolution in differential real-time kinematic (RTK) processing is affected by inter-frequency phase biases (IFPBs). Previous studies empirically determined that IFPBs are linearly dependent on the frequency channel number and calibration values have been derived to mitigate these biases for geodetic receivers. The corresponding IFPB-constrained model is currently the de facto approach in RTK, but the growing market of GNSS receivers, and especially low-cost receivers, makes calibration and proper handling of metadata a complex endeavor. Since IFPBs originate from timing offsets occurring between the carrier phase and the code measurements, we confirm other studies that show that IFPBs are not exactly linearly dependent on the frequency channel number, but rather linearly dependent on the channel wavelength, which calls for a modification in the GLONASS functional model. As an alternative to calibration, we revisit a calibration-free method for GLONASS ambiguity resolution and provide new insights into its applicability. A practical experiment illustrates that the calibration-free approach can offer better ambiguity fixing performance when the uncertainty on the IFPB parameter is large, unless partial ambiguity resolution is performed.




Similar content being viewed by others
References
Aggrey J, Bisnath S (2016) Dependence of GLONASS pseudorange interfrequency bias on receiver-antenna combination and impact on precise point positioning. Navigation 63(4):377–389. https://doi.org/10.1002/navi.168
Al-Shaery A, Zhang S, Rizos C (2013) An enhanced calibration method of GLONASS inter-channel bias for GNSS RTK. GPS Solut 17(2):165–173. https://doi.org/10.1007/s10291-012-0269-5
Banville S, Collins P, Lahaye F (2013) GLONASS ambiguity resolution of mixed receiver types without external calibration. GPS Solut 17(3):275–282. https://doi.org/10.1007/s10291-013-0319-7
Collins P, Bisnath S, Lahaye F, Héroux P (2010) Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. Navigation 57(2):123–135
de Bakker PF (2017) Static single-frequency multi-GNSS data (in binary u-blox format) and PPP corrections (ascii). 4TU.ResearchData. https://doi.org/10.4121/uuid:32cdf2e8-2243-443f-a3c0-09abbe5cae2f
de Bakker PF, Tiberius CCJM (2017) Real-time multi-GNSS single-frequency precise point positioning. GPS Solut 21(4):1791–1803. https://doi.org/10.1007/s10291-017-0653-2
Defraigne P, Bruyninx C (2007) On the link between GPS pseudorange noise and day-boundary discontinuities in geodetic time transfer solutions. GPS Solut 11(4):239–249. https://doi.org/10.1007/s10291-007-0054-z
Felhauer T (1997) On the impact of RF front-end group delay variations on GLONASS pseudorange accuracy. IN: Proceedings of ION GPS 1997, Institute of Navigation, Kansas City, Missouri, USA, Sep 16–19, pp 1527–1532
Geng J, Zhao Q, Shi C, Liu J (2017) A review on the inter-frequency biases of GLONASS carrier phase data. J Geod 91(3):329–340. https://doi.org/10.1007/s00190-016-0967
Habrich H, Beutler G, Gurtner W, Rothacher M (1999) Double difference ambiguity resolution for GLONASS/GPS carrier phase. In: Proceedings of ION GPS 1999, Nashville, Tennessee, USA, Sep 14–17, pp 1609–1618
Landau H, Euler HJ (1992) On-the-fly ambiguity resolution for precise differential positioning. In: Proceedings of ION GPS 1992, Albuquerque, New Mexico, USA, Sept 16–18, pp 607–613
Lanyi GE, Roth T (1988) A comparison of mapped and measured total ionospheric electron content using global positioning system and beacon satellite observations. Radio Sci 23(4):483–492. https://doi.org/10.1029/RS023i004p00483
Mader G, Beser J, Leick A, Li J (1995) Processing GLONASS carrier phase observations—theory and first experience. In: Proceedings of ION GPS 1995, Palm Springs, California, USA, Sep 12–15, pp 1041–1047
Odijk D, Wanninger L (2017) Differential positioning. In: Teunissen PJG, Montenbruck O (eds) Springer handbook of global navigation satellite systems, 1st ed. https://doi.org/10.1007/978-3-319-42928-1
Shi C, Yi W, Song W, Lou Y, Yao Y, Zhang R (2013) GLONASS pseudorange inter-channel biases and their effects on combined GPS/GLONASS precise point positioning. GPS Solut 17(4):439–451. https://doi.org/10.1007/s10291-013-0332-x
Sleewaegen JM, Simsky A, de Wilde W, Boon F, Willems T (2012) Demystifying GLONASS inter-frequency carrier phase biases. InsideGNSS 7(3):57–61
Takac F (2009) GLONASS inter-frequency biases and ambiguity resolution. InsideGNSS 4(2):24–28
Teunissen PJG (1993) Least-squares estimation of the integer GPS ambiguities. Technical report, LGR series 6, Delft Geodetic Computing Centre, Delft University of Technology, Delft, The Netherlands
Teunissen PJG (1995) The invertible GPS ambiguity transformations. Manuscr Geodaet 20(6):489–497
Teunissen PJG (1998) Success probability of integer GPS ambiguity rounding and bootstrapping. J Geod 72(10):606–612. https://doi.org/10.1007/s001900050199
Teunissen PJG, Odijk D (1997) Ambiguity dilution of precision: definition, properties and application. In: Proceedings of ION GPS 1997, Kansas City, Missouri, USA, Sep 16–19, pp 891–899
Tian Y, Ge M, Neitzel F (2015) Particle filter-based estimation of interfrequency phase bias for real-time GLONASS integer ambiguity resolution. J Geod 89(13):1145–1158. https://doi.org/10.1007/s00190-015-0841-1
Urlichich Y, Subbotin V, Stupak G, Dvorkin V, Povalyaev A, Karutin S (2011) GLONASS modernization. In: Proceedings of ION GNSS 2011, Portland, Oregon, USA, Sep 20–23, pp 3125–3128
Wang J, Rizos C, Stewart MP, Leick A (2001) GPS and GLONASS integration: modelling and ambiguity resolution issues. GPS Solut 5(1):55–64. https://doi.org/10.1007/PL00012877
Wanninger L (2012) Carrier phase inter-frequency biases of GLONASS receivers. J Geod 86(2):139–148. https://doi.org/10.1007/s00190-011-0502-y
Wanninger L, Wallstab-Freitag S (2007) Combined processing of GPS, GLONASS, and SBAS code phase and carrier phase measurements. IN: Proceedings of ION GNSS 2007, Fort Worth, Texas, USA, Sep 25–28, pp 866–875
Yamada H, Takasu T, Kubo N, Yasuda A (2010) Evaluation and calibration of receiver inter-channel biases for RTK-GPS/GLONASS. In: Proceedings of ION GNSS 2010, Portland, Oregon, USA, Sep 21–24, pp 1580–1587
Yao Y, Hu M, Xu X, He Y (2017) GLONASS inter-frequency phase bias rate estimation by single-epoch or Kalman filter algorithm. GPS Solut 21(4):1871–1882. https://doi.org/10.1007/s10291-017-0660-3
Acknowledgements
The authors would like to acknowledge the Geodetic Research Laboratory at UNB for sharing GNSS data from their continuously operating receivers. The initiative of Peter F. de Bakker to openly share his u-blox data is greatly appreciated. The constructive comments of an anonymous reviewer and the editor contributed in improving the original manuscript. This paper is published under the auspices of the NRCan Earth Sciences Sector as contribution number 20170171.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The derivations for the calibration-free model presented in previous sections are based on the assumption that IFPBs originate from the DCPB. This appendix presents an alternate derivation showing that the method can also cancel IFPBs present in carrier phase observations, provided that they can be modeled with a partial derivative taking the form of \(\lambda^{n} k^{n}\), such that:
Selecting a first reference satellite allows for the definition of the biased receiver clock:
The second reference satellite enables the estimation of the biased ambiguity of the reference satellite such that:
with
Inserting (51) and (53) into (50) leads to:
where \(\bar{N}_{AB}^{1n}\) has the same definition as (20) and:
By recognizing that:
the term \(\omega\) cancels from (54) and leads to a consistent system similar to (24)–(26). The only differences are the definition of the estimable receiver clock and reference ambiguity parameters, as shown by (51) and (53), respectively, while the definition of the estimable integer ambiguities remains unchanged.
Rights and permissions
About this article
Cite this article
Banville, S., Collins, P. & Lahaye, F. Model comparison for GLONASS RTK with low-cost receivers. GPS Solut 22, 52 (2018). https://doi.org/10.1007/s10291-018-0712-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-018-0712-3