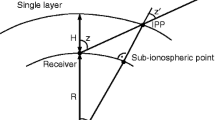
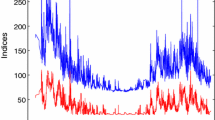
Abstract
Ionospheric delays compensation is a mandatory step for precise absolute and relative positioning of Low Earth Orbit Satellites (LEO) by GPS measurements. The most frequently used ionosphere model for real-time GPS-based navigation in LEO is an isotropic model proposed by Lear, which uses the Vertical Total Electron Content (VTEC) above the receiver and a mapping function for TEC evaluation along a given ray path. Based on significant assessed results available for ground-based GPS receivers, we propose the use of a different model relying on the thin shell assumption and a bilinear horizontal variation of the VTEC as a function of latitude and longitude in the shell. It is expected that this model is capable of better describing horizontal gradients in the ionosphere, thus improving ionospheric delay estimation, especially in intense ionospheric conditions. This model is referred to as Linear Thin Shell (LTS). LTS performance in estimating undifferenced and double-differenced ionospheric delays is checked by comparing measured and predicted delays computed using flight data from the GRACE mission. Results show that the LTS always outperforms the isotropic model, especially in case of high solar activity. Moreover, the LTS model provides a higher performance uniformity over a wide range of ionospheric delays, thus ensuring good performance in different conditions. The results obtained demonstrate that the LTS model improves the ionosphere delays estimation accuracy by 20 and 40% for undifferenced and double-differenced delays, respectively. This suggests the LTS model can effectively contribute to improving precision in LEO positioning applications.
















Similar content being viewed by others
References
Allain DJ, Mitchell CN (2009) Ionospheric delay corrections for single-frequency GPS receivers over Europe using tomographic mapping. GPS Solut 13(2):141–151. https://doi.org/10.1007/s10291-008-0107-y
Allende-Alba G, Montenbruck O (2016) Robust and precise baseline determination of distributed spacecraft in LEO. Adv Space Res 57(1):46–63. https://doi.org/10.1016/j.asr.2015.09.034
Allien A, Taillandier C, Capo C, Priselow K, Legenne J, Marechal J, Jeannot M (2011) User guide for EGNOS application developers, 2nd edn. Office for Official Publications of the European Communities, Luxembourg
Banville S, Zhang W, Ghoddousi-Fard R, Langley RB (2012) Ionospheric monitoring using “integer-levelled” observations. In: Proceedings of ION GNSS 2013, Institute of Navigation, Nashville, Tennessee, USA, 16–20 September, pp 2692–2701
Dach R, Schaer S, Arnold D, Prange L, Susnik A, Villiger A, Jäggi A (2016) CODE final product series for the IGS. http://boris.unibe.ch/96351. Accessed 14 June 2017
Ebinuma T, Bishop RH, Lightsey EG (2003) Integrated hardware investigations of precision spacecraft rendezvous using the global positioning system. J Guid Control Dyn 26(3):425–433. https://doi.org/10.2514/2.5080
Farrell J (2008) Aided navigation: gps with high rate sensors, 1st edn. McGraw-Hill Inc, New York
Gill E, D’Amico S, Montenbruck O (2007) Autonomous formation flying for the PRISMA mission. J Spacecr Rockets 44(3):671–681. https://doi.org/10.2514/1.23015
Howe BM, Runciman K, Secan JA (1998) Tomography of the ionosphere: four-dimensional simulations. Radio Sci 33(1):109–128. https://doi.org/10.1029/97RS02615
Huang Z, Yuan H (2013) Analysis and improvement of ionospheric thin shell model used in SBAS for China region. Adv Space Res 51(11):2035–2042. https://doi.org/10.1016/j.asr.2012.12.018
Jin R, Jin S, Feng G (2012) M_DCB: matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut 16(4):541–548. https://doi.org/10.1007/s10291-012-0279-3
Klobuchar JA (1987) Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans Aerosp Electron Syst AES 23(3):325–331. https://doi.org/10.1109/taes.1987.310829
Klobuchar JA (1996) Ionospheric effects on GPS. In: Parkinson BW, Spilker JJ (eds) Global positioning system: theory and applications, vol I. American Institute of Aeronautics and Astronautics Inc., Washington, pp 485–515
Komjathi A, Langley RB (1996) An assessment of predicted and measured ionospheric total electron content using a regional GPS network. In: Proceedings of ION NTM 1996, Santa Monica, California USA, 22–23 January, pp 615–624
Krieger G, Moreira A, Fiedler H, Hajnsek I, Werner M, Marwan Y, Zink M (2007) TanDEM-X: a satellite formation for high-resolution SAR interferometry. IEEE Trans Geosci Remote 45(11):3317–3340. https://doi.org/10.1109/TGRS.2007.900693
Kroes R, Montenbruck O, Bertiger W, Visser P (2005) Precise GRACE baseline determination using GPS. GPS Solut 9(1):21–31. https://doi.org/10.1007/s10291-004-0123-5
Lear WM (1988) GPS navigation for low earth orbiting vehicles. NASA 87-FM-2, Rev. 1, JSC-32031, Lyndon B. Johnson Space Center, Mission planning and analysis division
Leung S, Montenbruck O (2005) Real-time navigation of formation-flying spacecraft using global-positioning-system measurements. J Guid Control Dyn 28(2):226–235. https://doi.org/10.2514/1.7474
Liu J, Cannon ME, Alves P, Petrovello MG, Lachapelle G, MacGougan G, deGroot L (2003) A performance comparison of single and dual frequency GPS ambiguity resolution strategies. GPS Solut 7(2):87–100. https://doi.org/10.1007/s10291-003-0057-3
Mannucci AJ, Iijima BA, Lindqwister UJ, Pi X, Sparks L, Wilson BD (1999) GPS and ionosphere. In: Ross Stone W (ed) The review of radio science 1996–1999. Oxford University Press, New York, pp 625–665
Mitch RH, Psiaki ML, Tong DM (2013) Local ionosphere model estimation from dual-frequency global navigation satellite system observables. Radio Sci 48(6):671–684. https://doi.org/10.1002/2013RS005153
Mohiuddin S, Psiaki ML (2008) Carrier-phase differential global positioning system navigation filter for high-altitude spacecraft. J Guid Control Dyn 31(4):801–814. https://doi.org/10.2514/1.33948
Montenbruck O (2003) Kinematic GPS positioning of LEO satellites using ionosphere-free single frequency measurements. Aerosp Sci Technol 7:396–405. https://doi.org/10.1016/S1270-9638(03)00034-8
Montenbruck O, D’Amico S (2013) GPS based relative navigation. In: D’Errico M (ed) Distributed space missions for earth system monitoring. Springer, New York, pp 185–223
Montenbruck O, Ramos-Bosch P (2008) Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut 12(3):187–198. https://doi.org/10.1007/s10291-007-0080-x
Nava B, Coïsson P, Radicella SM (2008) A new version of the NeQuick ionosphere electron density model. J Atmos Solar-Terr Phys 70(15):1856–1862. https://doi.org/10.1016/j.jastp.2008.01.015
Odijk D (2003) Ionosphere-free phase combinations for modernized GPS. J Sur Eng ASCE 129(4):165–173. https://doi.org/10.1061/(ASCE)0733-9453(2003)129:4(165)
Odijk D, Teunissen PJG (2010) Improving the speed of CORS Network RTK ambiguity resolution. In: Proceedings of ION PLANS 2010, Indian Wells, California, USA, 4–6 May, pp 79–84. https://doi.org/10.1109/plans.2010.5507203
Rawer K (1988) Synthesis of ionospheric electron density profiles with Epstein functions. Adv Space Res 8(4):191–199. https://doi.org/10.1016/0273-1177(88)90239-6
Sardón E, Zarraoa N (1997) Estimation of total electron content using GPS data: how stable are the differential satellite and receiver instrumental biases? Radio Sci 32(5):1899–1910. https://doi.org/10.1029/97RS01457
Shi C, Gu S, Lou Y, Ge M (2012) An improved approach to model ionospheric delays for single-frequency Precise Point Positioning. Adv Space Res 49(12):1698–1708. https://doi.org/10.1016/j.asr.2012.03.016
Skone S, Cannon ME (1998) Auroral zone ionospheric considerations for WADGPS. J Navig 45(2):117–127. https://doi.org/10.1002/j.2161-4296.1998.tb02376.x
Spilker JJ (1996) GPS navigation data. In: Parkinson BW, Spilker JJ (eds) Global positioning system: theory and applications, vol I. American Institute of Aeronautics and Astronautics Inc., Washington, pp 230–257
Tancredi U, Renga A, Grassi M (2011) Ionospheric path delay models for spaceborne GPS receivers flying in formation with large baselines. Adv Space Res 48(3):507–520. https://doi.org/10.1016/j.asr.2011.03.041
Tancredi U, Renga A, Grassi M (2014a) Real-time relative positioning of spacecraft over long baselines. J Guid Control Dyn 37(1):47–58. https://doi.org/10.2514/1.61950
Tancredi U, Renga A, Grassi M (2014b) Geometric total electron content models for topside ionospheric sounding. In: Proceedings of EESMS 2014—2014 IEEE workshop on environmental energy and structural monitoring systems, 17–18 September, pp 163–168. https://doi.org/10.1109/eesms.2014.6923285
Tancredi U, Renga A, Grassi M (2014c) Novel closed-loop approaches for precise relative navigation of widely separated GPS receivers in LEO. Acta Astronaut 93:243–251. https://doi.org/10.1016/j.actaastro.2013.07.029
Tancredi U, Allende-Alba G, Renga A, Montenbruck O, Grassi M (2015) Relative positioning of spacecraft in intense ionospheric conditions by GPS. Aerosp Sci Technol 43:191–198. https://doi.org/10.1007/s10291-003-0055-5
Tapley BD, Bettadpur S, Watkins M, Reigber C (2004) The gravity recovery and climate experiment: mission overview and early results. Geophys Res Lett. https://doi.org/10.1029/2004GL019920
Teunissen PJG (1997) The geometry-free GPS ambiguity search space with a weighted ionosphere. J Geodesy 71(6):370–383. https://doi.org/10.1007/s001900050105
van Barneveld PWL, Montenbruck O, Visser PN (2007) Differential ionospheric effects in GPS based navigation of formation flight satellites. In: Proceedings of 3rd international symposium on formation flying, Mission and Technology 2008, ESA/ESTEC, Noordwijk, The Netherlands, 23–25 April, pp 1–8
Verhagen S, Odijk D, Teunissen PJG, Huisman L (2010) Performance improvement with low-cost multi-GNSS receivers. In: Proceedings of NAVITEC 2010, Noordwijk, The Netherlands, 8–10 December, pp 1–8. https://doi.org/10.1109/navitec.2010.5708015
Verhulst T, Stankov SM (2015) Ionospheric specification with analytical profilers: evidences of non-Chapman electron density distribution in the upper ionosphere. Adv Space Res 55(8):2058–2069. https://doi.org/10.1016/j.asr.2014.10.017
Zhang W, Langley RB, Komjathi A, Banville S (2013) Eliminating potential errors caused by the thin shell assumption: an extended 3D UNB ionospheric modelling technique. In: Proceedings of ION GNSS 2013, Institute of Navigation, Nashville, Tennessee, USA, 16–20 September, pp 2447–2462
Zhong J, Lei J, Dou X, Yue X (2016a) Assessment of vertical TEC mapping functions for space-based GNSS observations. GPS Solut 20(3):353–362. https://doi.org/10.1007/s10291-015-0444-6
Zhong J, Lei J, Yue X, Dou X (2016b) Determination of differential code bias of GNSS receiver onboard low earth orbit satellite. IEEE Trans Geosci Remote 54(8):4896–4905. https://doi.org/10.1109/TGRS.2016.2552542
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Renga, A., Causa, F., Tancredi, U. et al. Accurate ionospheric delay model for real-time GPS-based positioning of LEO satellites using horizontal VTEC gradient estimation. GPS Solut 22, 46 (2018). https://doi.org/10.1007/s10291-018-0710-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-018-0710-5