Simulation and evaluation of the distribution of interest rate risk

Abstract

We study methods to simulate term structures in order to measure interest rate risk more accurately. We use principal component analysis of term structure innovations to identify risk factors and we model their univariate distribution using GARCH-models with Student’s t-distributions in order to handle heteroscedasticity and fat tails. We find that the Student’s t-copula is most suitable to model co-dependence of these univariate risk factors. We aim to develop a model that provides low ex-ante risk measures, while having accurate representations of the ex-post realized risk. By utilizing a more accurate term structure estimation method, our proposed model is less sensitive to measurement noise compared to traditional models. We perform an out-of-sample test for the U.S. market between 2002 and 2017 by valuing a portfolio consisting of interest rate derivatives. We find that ex-ante Value at Risk measurements can be substantially reduced for all confidence levels above 95%, compared to the traditional models. We find that that the realized portfolio tail losses accurately conform to the ex-ante measurement for daily returns, while traditional methods overestimate, or in some cases even underestimate the risk ex-post. Due to noise inherent in the term structure measurements, we find that all models overestimate the risk for 10-day and quarterly returns, but that our proposed model provides the by far lowest Value at Risk measures.

1 Introduction

Interest rate risk is an important topic for both risk management and optimal portfolio management. The theory of measuring interest rate risk has evolved from dealing with sensitivity to risk factors, and immunization against risk, to a more modern view, where a better understanding of the actual risk factors is used in order to generate possible outcomes of risk factors. This paper takes the perspective of measuring interest rate risk by simulating future term structure scenarios, and ensuring that these properly describe the observed realizations. Interest rate risk has not always been properly connected to the term structure of interest rates. Bond duration, introduced by Macaulay (1938), was originally defined as bond sensitivity to discount factors. For the sake of simplicity, Macaulay (1938) chose to discount using yield to maturity, see Ingersoll et al. (1978) and Bierwag et al. (1983) for further details. A significant constraint when defining duration in terms of yield to maturity is that it cannot be used as a risk proxy unless the term structure is flat, as shown by Ingersoll et al. (1978). The interest rate risk was not properly linked to movements in the term structure until Fisher and Weil (1971) provided a proof of how to construct an immunized bond portfolio by choosing the duration of a portfolio equal to the investment horizon. This proof was carried out through a constant parallel shift of the term structure of forward rates. The view of interest rate risk as the sensitivity to certain perturbations in the term structure led to many suggestions of risk factors to be used in order to handle non-parallel risk, some of which we will describe in Sect. 4. However, modern risk concepts used in the Basel regulations are evolving towards measuring risk as outcomes of possible shocks to the risk factors. The way of measuring this risk is advancing, from Value at Risk (VaR), to the similar but coherent risk measure; expected shortfall (ES), see Chang et al. (2016) and the FRTB document from the Basel Committee on Banking Supervision (2014). The computation of ES usually requires simulation of potential outcomes of identified risk factors, although historical simulation might be an option. In this paper, we model risk through estimating the univariate distribution of risk factors and using copulas in order to model their co-dependence.

We choose to study the interest rate derivative market, instead of the bond market, where credit risk and liquidity cause additional problems for interest rate risk measurement. We use principal component analysis (PCA), which is a common, data driven, way of identifying risk factors in the interest rate market, see Litterman and Scheinkman (1991) and Topaloglou et al. (2002). We show that performing PCA on term structures estimated by bootstrapping and Cubic spline interpolation, results in problems of determining the systematic risk factors, which affects the results of the risk measurement. Instead, we wish to examine the possibility of improving risk measurement by utilizing an accurate method of measuring forward rate term structures, developed by Blomvall (2017). The well-established method proposed by Nelson and Siegel (1987) is also added for comparison. This method is commonly used in the bond market in order to mitigate noise problems, and dynamic extensions have been used in term structure forecasting by Diebold and Li (2006) and Chen and Li (2011). It has also been used for risk simulation, by Abdymomunov and Gerlach (2014) and Charpentier and Villa (2010).

In the light of the new, and the upcoming Basel regulations, we conclude that measuring interest rate risk through risk factor simulation is an important topic where literature is not very extensive. We also note that most papers evaluate different risk models using tail risk by studying the number of breaches in a VaR or ES setting, see e.g. Rebonato et al. (2005). While this is relevant for compliance of the regulations, it does not reflect the entire distribution, which is of importance for other applications, such as hedging or portfolio management. This paper thus focuses on the method of simulating term structure scenarios in order to accurately measure interest rate risk throughout the entire value distribution. We use VaR as a special case in order to illustrate differences in risk levels between the models. We find that three properties are of importance when measuring interest rate risk. First, there should be no systematic price errors caused by the term structure estimation method. Second, the distribution of the risk factors must be consistent with their realizations. Third, lower risk is preferable. This paper aims to develop models that satisfy all three properties, which proves to be a difficult task, especially for long horizons. This was also observed by Rebonato et al. (2005), where they had to rely on heuristic methods. In contrast, our aim is to use the extracted risk factors for risk measurement over different horizons. However, this paper does not focus on long term scenario generation over years or decades.

The paper is disposed as follows. In Sect. 2 we discuss how to estimate the term structures, using the data described in Sect. 3. We use PCA to extract systematic risk factors, and their properties are studied in Sect. 4. We use GARCH models together with copulas to model the evolution of these risk factors, which we describe in Sects. 5 and 6. The model evaluation is carried out by simulating term structure scenarios from different models, and using these scenarios to value portfolios consisting of interest rate derivatives. The values of the generated scenarios for each day are compared to portfolio values of the realized historical term structures. We describe this procedure together with the statistical tests used for comparison in Sect. 7. The results are presented in Sect. 8, followed by conclusions in Sect. 9.

2 Term structure estimation

Interest rate risk originates from movements in the term structure of interest rates. The term structure of interest rates is not directly observable, but has to be measured by solving an inverse problem based on observed market prices. However, these prices contain measurement noise, arising from market microstructure effects, as described by Laurini and Ohashi (2015). An important aspect of a well-posed inverse problem is that small changes in input data should result in small changes in output data. Hence, a term structure measurement method should not be sensitive to measurement noise in observed market prices.

Term structure measurement methods can be divided into exact methods and inexact methods. Exact methods will reprice the underlying financial instruments used to construct the curve exactly, and use some interpolation method to interpolate interest rates between the cash flow points belonging to those instruments. The fact that exact methods reprice all in-sample instruments exactly, makes them very sensitive to measurement noise in the market prices, as pointed out by Blomvall (2017). Inexact methods often assume that the term structure can be parametrized by some parametric function, and use the least square method to find these parameters. Inexact methods are less sensitive to measurement noise, but the limitations on the shape enforced by the parametric functions often lead to systematic price errors. Parametric methods include the parsimonious model by Nelson and Siegel (1987), and the extension by Svensson (1994). A way of extending interpolation methods to deal with noise is the recent application of kringing models by Cousin et al. (2016). This method can be adapted both for exact interpolation, or best fitting of noisy observations.

Blomvall (2017) presents a framework for measuring term structures though an optimization model that can be specialized to a convex formulation of the inverse problem. The framework is a generalization of previously described methods from literature, and is based on a trade-off between smoothness and price errors, which is accomplished by discretization and regularizations of the optimization problem. Blomvall and Ndengo (2013) compare this method to traditional methods, and show that it dominates all the compared traditional methods with respect to out-of-sample repricing errors. They also demonstrate a connection between in-sample price errors and interest rate risk, measured by the sum of variance in the curve. From this study, it is evident that low risk (variance) cannot be achieved in combination with low in-sample pricing errors. Each trading desk thus faces a decision of what level of risk, and what level of price errors should be acceptable according to laws and regulations.

The methodology in this paper will primarily be based around the generalized framework by Blomvall (2017), which we will use to measure daily discretized forward rate term structures directly. Two other term structure measurement methods will be used as reference methods in the comparison. The first one is the dynamic extension of Nelson and Siegel (1987), which was introduced by Diebold and Li (2006), and has been popular in literature of term structure forecasting. The other method is bootstrapping interest rates and interpolating spot rates using natural Cubic splines, which according to Hagan and West (2006) is commonly used by practitioners.

In order to reduce the dimensionality of the problem of measuring the risk inherent in the high dimensional term structures, we will measure the risk of a portfolio consisting of interest rate derivatives. The portfolio consists of forward rate agreements (FRA) and is set up to mimic the behavior of the FRA book of a bank. Forward rate agreements are traded in huge amounts on the OTC market, where all major banks hold a trading book of these instruments. This book is the direct result of trades with customers who want to swap their payment streams between fixed and floating interest rates at some point in the future. Banks act market makers for this market, making profit on the spread between bid and ask yields. Taking on risk is an undesirable side effect of this business. We have also been studying interest rate swaps alongside forward rate agreements, but their pricing function only depend on spot rates, which makes them less sensitive to forward rates due to the inherent integrating mechanism of spot rates. Since, we we seek a model which is able to explain the interest rate risk inherit in forward rates as well as spot rates, we do not focus on swaps in this paper. The portfolio composition is randomly generated, and the details of this are presented in Sect. 7.

Fig. 1

The left panel shows portfolio values for the forward rate agreement portfolio. The portfolio values are almost indistinguishable, and hence we show the difference in portfolio values compared to the median portfolio value for each day in the right panel

Table 1 Portfolio volatilities based on differences of the portfolio values from left panel of Fig. 1, and standard deviations of the series from the right panel of Fig. 1

By using term structures estimated by the three methods described above, we price the portfolio. For the Blomvall (2017) method, we have used the parameters of the LSExp model described in Blomvall and Ndengo (2013), where we only penalize the discrete version of the second order derivative with exponential weights according to

$$\begin{aligned} w^{ (2)}_t = \left\{ \begin{array}{ll} e^{\left( \frac{t}{365}-2\right) \ln 4}, &{} \text {if} \, t \le 730 \, \text {days},\\ 1, &{}\text {if}\, t > 730 \,\text {days},\end{array}\right. \end{aligned}$$

(1)

scaled with a penalty parameter $P=10$. For the Nelson and Siegel (1987) model we have fixed the parameter $\lambda = 0.0609$ as suggested by Diebold and Li (2006) and others. The choice of this parameter is based on making the third risk factor reach its maximum at the maturity of 30 months.

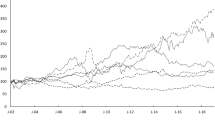
The portfolio values can be found in the left panel of Fig. 1, and we note that all term structure estimation methods produce values that are seemingly consistent with each other most of the time. To further study the differences in portfolio values among these methods, without making any presumptions, we extract the median portfolio value out of the three methods for each day. One of the portfolios will thus equal the median value, and we assume that this value is the “correct” portfolio value. We then compare the value of each portfolio to this median to identify systematic price deviations, seen in the right panel of Fig. 1. By calculating the standard deviation of these series, we get a numeric estimate of the magnitude that each method deviates from the median value over the entire period. These values are presented in Table 1, together with portfolio volatilities and the number of days each method has attained the median value. We see that the Blomvall (2017) method has the lowest portfolio volatility and by far the lowest median deviation volatility, while it equals the median valuation most often. We interpret this as a sign of high consistency with market prices, which is one of our three desired properties when measuring risk. The Nelson and Siegel (1987) has low portfolio volatility but a high median deviation. This is due to its value drift away from the median value during long periods at a time, which we interpret this as a sign of systematic price errors due to the inflexible parametric nature of the model. In theory, the volatility of the portfolios can be divided into two unobservable components. The first, arising from movement in the systematic risk factors, and the second, arising from noise. The presence of both high portfolio values and high deviations for the Cubic spline method indicates that the additional portfolio volatility is caused by noise that is amplified by the interpolation method. These findings are also in line with the results by Blomvall and Ndengo (2013). We will later see how this noise affects the shape of the systematic risk factors.

3 Data

The data used for estimating term structures in this study is retrieved from Thomson Reuters Eikon. We focus on the U.S. fixed income market due to its high liquidity and availability of data. The data consists of time series for a 3 month USD LIBOR rate, ten annually spaced interest rate swaps, (Table 2), and twelve forward rate agreements (Table 3). The time series, containing bid and ask yields, range from 1996 to 2017, and are divided into an in-sample period (1996-01-02 to 2001-12-30), used for fitting proper models to this data, and an out-of-sample period (2002-01-04 to 2017-07-01) used for the analysis of the interest rate risk for the portfolio. The data series have a few gaps, where data from one or more instruments is missing. Since this has a big impact on the estimation of term structures, we remove the dates for which the number of missing quotes exceeds the 10-day moving average of missing quotes, plus one. This cleaning process removes 24 out of 5512 days from the estimation. Of the remaining days, 1599 belong to the in-sample period and 3889 belong to the out-of-sample period.

Table 2 Interest rate swaps included in term structure measurement

Table 3 Forward rate agreements included in term structure measurement

4 Systematic risk factors

In this section we will present our view of risk measurement as a general framework, and how to utilize it for the purpose of measuring interest rate risk. We start by considering a portfolio consisting of n assets, where the price of an asset $P_i({\varDelta }\xi )$ depends on the state of m random risk factors ${\varDelta }\xi \in {\mathbb {R}} ^{m \times 1}$. A second order Taylor approximation of the asset value around the current risk levels gives us

$$\begin{aligned} P_i({\varDelta }\xi ) \approx P_i(0) + g_i^T {\varDelta }\xi + \frac{1}{2} {\varDelta }\xi ^T H_i {\varDelta }\xi \end{aligned}$$

(2)

where

$$\begin{aligned} g_i&= \nabla _{{\varDelta }\xi } P_i \vert _{{\varDelta }\xi = 0}, \end{aligned}$$

(3)

$$\begin{aligned} H_i&= \nabla _{{\varDelta }\xi }^2 P_i \vert _{{\varDelta }\xi = 0} . \end{aligned}$$

(4)

The total value of the portfolio with holdings $h \in {\mathbb {R}} ^{n \times 1}$ is dependent on these risk factors according to

$$\begin{aligned} V(h, {\varDelta }\xi ) = \sum \limits _{i=1}^n h_i P_i({\varDelta }\xi ) . \end{aligned}$$

(5)

This raises the question of which systematic risk factors to use in the analysis. A number of options have been presented in literature. Fisher and Weil (1971) present the duration concept in terms of a parallel shift in forward rates. By extending the parallel shift of duration to general functions, duration vector models are formed. One possibility here is to use polynomial functions of the form $t^{i-1}$ as proposed by Prisman and Shores (1988) and Chambers et al. (1988). Another possibility is to use the exponential functions for level, slope and curvature from the term structure model by Nelson and Siegel (1987). This approach, which has been studied by Willner (1996) and Diebold et al. (2004), will be used in this paper to model the risk factors of the Nelson and Siegel (1987) model.

A different, data-driven approach for identifying systematic risk factors is principal component analysis (PCA). This method can be used to approximate the covariance matrix of a dataset by finding a set of orthogonal components that maximize the variance. PCA was first applied to term structures of interest rates by Litterman and Scheinkman (1991). This study was later followed by Knez et al. (1994) and Bliss (1997), among others. An alternative approach for feature extraction is independent component analysis (ICA). While PCA aims to explain the second order information, i.e. the variance, ICA tries to maximize independence in higher orders as well. As a result, the factors obtained from ICA will be independent; while factors obtained from PCA only will be uncorrelated, unless the data follows a Gaussian distribution. In contrast, ICA assumes a non-normal distribution in order to be able to separate the independent sources since it maximizes non-Gaussianity of the components (Chen et al. 2007). A weakness of ICA is that the factors cannot be ordered in terms of importance, while PCA factors are ordered in terms of explained variance. In fact, the variance of the ICA factors cannot be determined in a unique way (Moraux and Villa 2003). Dealing with risk is directly related to dealing with variance, and since PCA factors are orthogonal, they also provide a natural interpretation (Molgedey and Galic 2001). While the less restrictive assumptions of ICA are appealing for non-Gaussian financial data, more recent applications of ICA to interest rates, especially of higher dimensionality, are missing in literature. Hence, PCA will be used to extract risk factors in this paper.

In order to extract risk factors using PCA, we have to discretize the term structures to compute the covariance matrix. The output of the Blomvall (2017) method is daily discretized forward rate term structures, $f_{t,T}$, which can be used directly. For the Cubic spline method, we perform a discretization to daily spot rates $s_{t,T}$. To convert term structures between forward rates and spot rates we use

$$\begin{aligned} f_{t,T} = \frac{s_{t,T} \tau _T - s_{t,T-1} \tau _{T-1}}{\tau _T - \tau _{T-1}}, \quad s_{t,T} = \frac{f_{t,T} \left( \tau _T - \tau _{T-1} \right) + s_{t,T-1} \tau _{T-1}}{\tau _T} . \end{aligned}$$

(6)

We have to decide whether to use the covariance matrix of spot rates or forward rates, and whether to use the interest rate levels or their innovations. Since risk is connected to changes in the term structure, rather than its levels, we believe that daily absolute innovations of interest rates should be used rather than levels in order to explain risk. We choose the covariance matrix instead of correlation since innovations are of similar magnitude across maturities, and we seek to explain this magnitude as well as the correlation. Forward rates contain the most local information, since spot rates are averages of forward rates. Forward rates are also the expectation of the future short rate, under the T-forward measure, implying that changes in forward rates should be linked to the flow of information. Additionally, the risk factors of the central HJM model (Heath et al. 1992), are derived in terms of forward rates and forward rate volatility, which is why it would be ideal to use forward rates. However, performing a PCA on forward rate innovations requires forward rate data of high quality, in order to be able to extract realistic risk factors. Laurini and Ohashi (2015) provide an excellent review of the topic, and highlight the problem with measurement errors in forward rates due to market microstructure effects. They present a proposition that the effective number of risk factors should be the same, regardless of the choice of underlying interest type. The fact that this cannot be observed in literature provides strong evidence for the prevalence of measurement noise in the data. Instead of directly addressing this problem of term structure measurement, Laurini and Ohashi (2015) address the problem by introducing a technique for estimating the covariance matrix in the presence of measurement noise, called the long-run covariance matrix.

We start by illustrating the risk factors resulting from performing a PCA on daily absolute differences of forward rate term structures, estimated with the Blomvall (2017) method, seen in the left panel of Fig. 2. Even though the analysis is carried out on forward rates, the risk factors do not indicate presence of noise. The corresponding forward rate risk factors, calculated for cubic spline interpolated spot rates, seem highly unrealistic due to its oscillating appearance, as seen in right panel of Fig. 2. The idea of explaining systematic risk using these kinds of oscillating risk factors is economically unappealing since there is no information that would predict such a distinct behavior. Instead, this is an artifact of the interpolation method between the yearly spaced knot points of the cubic spline. By performing the PCA on spot rates directly, as illustrated in the left panel of Fig. 3, one might believe that these risk factors would explain the risk far better than the forward rate based risk factors seen earlier. Fewer risk factors will indeed be needed to explain the same fraction of the covariance matrix, but the forward rate risk factors implied by these spot rate risk factors are still highly unrealistic, as seen in the right panel of Fig. 3.

Fig. 2

Risk factors for PCA carried out for forward rates

Fig. 3

Risk factors for PCA carried out for spot rates and their implied risk factors for forward rates

By studying the volatility in the spot rate curves, and its implications for the forward rate volatility, we get an understanding of what is going on under this transformation. If C denotes the $n \times n$ covariance matrix of forward rates, we compute the vector of term structure volatilities for each discrete maturity point as the element-wise square root of the diagonal elements of C

$$\begin{aligned} \sigma _f = \sqrt{\text {diag}(C)} . \end{aligned}$$

(7)

By approximating the covariance matrix from the first n eigenvectors, forming the matrix $E_{f_n}$, and a vector containing their corresponding eigenvalues, $\lambda _n$, we can compute the forward rate volatility explained by this approximation as

$$\begin{aligned} \sigma _{f_a} = \sqrt{ \text {diag}( E_{f_n} \text {diag}(\lambda _n) E_{f_n}^T ) } . \end{aligned}$$

(8)

Let us introduce the $n \times n$ matrix A,

$$\begin{aligned} A_{i,j} = {\left\{ \begin{array}{ll} 1/i, &{} \text {if}\ j \le i \\ 0, &{} \text {otherwise} , \end{array}\right. } \end{aligned}$$

(9)

which transforms a vector of forward rates into spot rates. In a similar way, we can introduce B, which is the inverse of A, and transforms spot rates to forward rates. Using B, we can compute the forward rate volatility implied by the spot rate risk factors as

$$\begin{aligned} \sigma _{s_a} = \sqrt{ \text {diag}(B E_{s_n} \text {diag}(\lambda _n) E_{s_n}^T B^T )} . \end{aligned}$$

(10)

Fig. 4

Term structure volatilities for different representations of the data. Since we are able to explain almost the entire covariance matrix in-sample, the long dashed lines will not be distinguishable from the solid lines. The eigenvectors of Cubic spline spot rates are not able to explain the entire variance of the forward rates using this limited set of risk factors

The result of these computations is illustrated in Fig. 4, and here it is evident that the term structures estimated from the Cubic spline method contain a lot of noise. The risk factors will, to a high degree, model this noise instead of the systematic risk in the market. This can be seen by comparing its forward rate volatility, $\sigma _f$, to the volatility of the Blomvall (2017) model. Studying the spot rate volatilities, in the left panel of Fig. 4, one gets the impression that the amount of volatility for the longer maturities is the same for both models. Performing the analysis on spot rates does not get rid of the noise, but rather hides it, as seen by the implied forward rate volatility $\sigma _{s_a}$. The volatility in forward rates is almost the same as when PCA is performed on the forward rate covariance matrix. This is due to the integrating property when converting forward rates to spot rates. For this reason, we study forward rate agreements rather than interest rate swaps, because of their price sensitivity to forward rates.

By taking this analysis one step further, we can examine what faction of the total variance we are able to explain by different risk factors. The results are shown in Fig. 5, and we immediately note that close to all of the in-sample variance is explained by six risk factors for the Blomvall (2017) data. We also note that the majority of the variance in the long end of the term structure is explained by the first three risk factors (shift, twist and butterfly). The movements in the short end of the curve are, on the other hand, explained by the following three components. For PCA based on forward rates of Cubic splines, a very large proportion of the variance in the maturity range between 6 months and 2 years remains unexplained by the first six risk factors. In total, as many as 16 risk factors are needed to achieve a similar degree of explained variance across all maturities. Performing the same analysis on spot rate based risk factors, arising from PCA of daily discretized Cubic splines, we conclude that ten risk factors are needed. We will thus include two Cubic spline-based models in the risk measurement evaluation. One using 16 risk factors for forward rate innovations, ${\varDelta }f_{t,T}$, and another using ten risk factors for spot rate innovations, ${\varDelta }s_{t,T}$, where

$$\begin{aligned} {\varDelta }f_{t,T} = f_{t,T} - f_{t-1,T}, \quad {\varDelta }s_{t,T} = s_{t,T} - s_{t-1,T} . \end{aligned}$$

(11)

Both are based on the same term structures, where the bootstrapping technique is combined with cubic spline interpolation. As explained earlier, the difference is that the PCA will be carried out on either discretized spot rates directly, or its corresponding forward rates. Modeling each risk factor using a normal distribution with a constant variance equal to its corresponding eigenvalues would yield similar results for these two models according to Fig. 4. However, we will use more sophisticated volatility models and copulas to model the relationship between the components, as described below. We will then get back to this volatility analysis using those models.

Fig. 5

Proportions of term structure variance explained by different risk factors

5 Volatility and scenario modeling

Volatility modeling of the equity market returns has been studied thoroughly, where several empirical properties have been documented, see Gavrishchaka and Banerjee (2006) and references therein. Equity returns have a very short-range autocorrelation, within time spans as small as a few minutes. Equity return volatility on the other hand, is found to be clustered with a long-range memory up to several months, while being mean-reverting. The distribution of returns is fat-tailed and leptokurtic at time frames up to a few days. Volatilities are also found to be negatively correlated with returns, called the leverage effect.

The above-mentioned properties imply that the classical assumption of normally distributed returns, with constant volatility, makes an inappropriate model for equity returns. Several models to deal with these properties have thus been proposed. Since this paper considers interest rate risk, and not equity risk, we seek to model changes in the interest rate risk factors rather than equity returns. We find that these properties are present also in the principal components of interest rate innovations, $y_t = E^T {\varDelta }f_t$. Studying the most significant principal component time series, it is evident that some of these properties are present here as well. The statistic tests that have been carried out to confirm this are: a normality test by Shapiro and Wilk (1965), a skewness test by Kim and White (2004) and a heteroscedasticity test by Engle (1982). The results of these tests for the six most significant forward rate based principal components of the Blomvall (2017) dataset are found in Table 4.

Table 4 Tests for stylized facts from the equity market applied to the six most significant principal component of Blomvall (2017) data

Deguillaume et al. (2013) empirically show that the interest rate volatility is dependent on the interest rate levels in certain regimes. For low interest rates, below 2%, and for high interest rates, above 6%, interest rate volatility increases proportionally to the interest rate level. For the regime of 2–6% however, the interest rate volatility does not seem to depend on the interest rate level. Although these are interesting findings, we choose to model interest rate volatility separated from interest rate levels. If the interest rate volatility is dependent on the current regime, a volatility model based on actual principal component changes will capture this behavior for these different regimes indirectly. This approach works regardless of the regime, even under negative interest rates. To model the observed stylized facts of the principal component series, we have implemented several models of the GARCH class, primarily based on the arch package for Python written by Sheppard (2017).

The simplest way to model volatility is the constant volatility model

$$\begin{aligned} \sigma _t = c. \end{aligned}$$

(12)

To handle the heteroscedasticity and skewness, a model based on the paper by Glosten et al. (1993), is applied. The GJR-GARCH(p, o, q) volatility process is given by

$$\begin{aligned} \sigma _t^2 = \omega + \sum \limits _{i=1}^p \alpha _i |y_{t-i}|^2 + \sum \limits _{j=1}^o \gamma _i |y_{t-j}|^2 I_{\left\{ y_{t-j} < 0 \right\} } + \sum \limits _{k=1}^q \beta _i \sigma _{t-k}^2. \end{aligned}$$

(13)

To model changes in the principal components, we propose different processes, based on the volatility processes above. The simplest one is to model a constant, or even assume a zero drift

$$\begin{aligned} y_t = \mu + \epsilon , \end{aligned}$$

(14)

where $\epsilon$ is a random number drawn from either the normal distribution, or the Student’s t-distribution, which is scaled by the volatility from (Eq. 13). Our findings suggest that the drift term is of very limited importance compared to the volatility, and that the constants become insignificant, as we will see in Table 6 later. Autoregressive processes are commonly used for the evolution of risk factors in the term structure forecasting literature. Define the AR(p)-model as

$$\begin{aligned} y_t = \mu + \sum \limits _{i=1}^p {\varPhi }_{L_i} y_{t-L_i} + \epsilon , \end{aligned}$$

(15)

where $L_i$ is the lag of order i. Autoregressive models of order $p=1$ are popular, since an autocorrelation is usually observed at lag one for the different principal components. However, there is no inherent mechanic in the fixed income market to justify this behavior. This is rather an effect of term structures adapting to measurement noise and returning back to the previous shape the following day. As a result of this, the use of autoregressive models to model general movements in principal components can be questioned. We believe that this autocorrelation effect should be prevented by the term structure measurement method directly, by utilizing information from adjacent days. This is, however, not yet integrated in the Blomvall (2017) framework, nor in any other term structure estimation method. We find that negative autocorrelations are present in the principal components, shown in Table 5. Even though this indicates that an AR(1) would improve our results, we have not been able to show any improvements by including autoregressive processes, which is why we do not present any AR results. We note that principal components based on Blomvall (2017) term structures have less autocorrelation than Cubic splines, especially in the most significant component, which is another indication that Cubic splines contain more noise.

Table 5 Autocorrelation for the ten most significant principal components for different methods, together with the proportion of the total variance explained by each eigenvector

5.1 Simulation of term structures

When the process for each principal component is given, we are able to simulate term structures using the Monte Carlo method. Consider the discrete term structure of forward rates $f_t$, observed at time t, and let $E_n$ denote the matrix of the n most significant eigenvectors from the PCA. If $y_t$ represents the simulated shocks for these n risk factors between the time point t and $t+1$, the forward rate term structure dynamics are given by

$$\begin{aligned} f_{t+1} = f_t + E_n y_t . \end{aligned}$$

(16)

It is worth pointing out that the Nelson and Siegel (1987) scenario generation model uses the exact same implementation to generate $y_t$ as the principal component based models, but applied to the parameter series $(\beta _0, \beta _1, \beta _2)$ of the parametric functions instead. An illustration of forward rate scenarios 1 day ahead is shown in Fig. 6, where we note a clear difference in terms of realism between the two models. When generating scenarios more than 1 day ahead, one of two techniques can be used. The first, and simplest one, is to forecast volatility analytically. This is carried out by setting the shocks $y_t$ to its expected value for the time points up to our simulation horizon. Using a zero mean model with a GARCH model, this means that we set the shocks to $y_t=0$, and let the volatility mean revert over the simulation horizon. We then simulate daily changes using this mean reverting path of the volatility, and sum the changes. The second approach is to simulate different paths for the volatility, where we use the simulated values $y_t$ to update the volatility process along its path for each scenario separately. This is far more time and memory consuming, but produces better results for simulation horizons longer than one day. Since volatility forecasting occupies only a part of the total time, we use the simulation-based volatility forecasts for horizons beyond one day.

Fig. 6

Example of 250 1-day-ahead term structure scenarios generated using the Blomvall (2017) model and Cubic spline model with forward rate risk factors for the date 15 January 2017. The thicker blue lines represent the term structure of the present date

5.2 Model fitting and calibration

All models are fitted using the Bayesian Information Criterion (BIC) in order to avoid overfitting and over-parameterization. This since BIC has a higher penalty for additional parameters than the Akaike Information Criterion (AIC) when the number of observations is large. BIC is used to determine the order of the GJR-GARCH(p, o, q), the constant and the order of lag of the autoregressive model, as well as the choice of residual distribution among normal and Student’s t. Different risk factors may have different model orders and use different distributions. The parameters attained for in-sample dataset can be found in Table 6, and we can observe that the same GARCH(1, 1)-model using a Student’s t distribution has been selected across all models. We also note that the drift term $\mu$ is insignificant for all the displayed parameters. The risk factors are estimated once, using 6 years of in-sample data between 1996 and 2001. The model parameters and copulas are recalibrated every 2 years, using new data but keeping the data window of 6 years fixed.

Table 6 Mean value and model parameters for the GARCH-process including degrees of freedom for the Student’s t-distribution together with their corresponding p values for the in-sample period

To illustrate some of the stylized facts of the risk factor changes, we study in-sample histograms for the normalized residuals for the three most significant risk factors computed from the forward rate risk factor model by Blomvall (2017), seen in Fig. 7. It is clear that the GARCH-type models provide a better fit constant volatility models. This should come as no surprise, since the data tested positive for heteroscedasticity. We also note that the Student’s t-distributed residuals have been selected over normally distributed ones, which also holds for less significant risk factors. These findings also confirm the stylized facts presented earlier.

Fig. 7

In-sample histograms during 1996–2001 for the three most significant risk factors from Blomvall (2017) model, using a constant volatility model (top) compared to a GARCH volatility model (bottom)

6 Modeling co-dependence via copulas

We have thus far described univariate models for the principal component time series. By construction, these series are uncorrelated for the in-sample data. If the input data were also normally distributed, they would be independent. As argued previously, the principal component series are not normally distributed, and hence not independent. In addition, the out-of-sample data used in the test will still be correlated to some degree. According to Kaut and Wallace (2011), copulas are able to capture such dependencies in non-normally distributed principal components, and we therefore apply copulas to deal with these dependencies.

Junker et al. (2006) study term structure dependence via copulas by investigating the long end and the short end of the term structure, represented by spot rates for 1-year and 5-year maturities respectively. They find that elliptical copulas, such as normal and Student-t copulas are not suitable for modeling this complex dependence structure. Instead, the class of Archimedean couplas, including Frank and Gumbal copulas, could capture this structure. Modeling two distinct interest rate levels differs from modeling the movement of several risk factors. We thus had very limited success using Archimedean copulas, where they worked at all for this high dimensional data, using the R-package by Hofert et al. (2017). The copulas are calibrated using principal component changes normalized by the volatility from our volatility models, since they are to be used to generate dependent random numbers used in the volatility process. The inverse cumulative distribution function for the chosen distribution of each risk factor is then used together with the copula, in order to generate dependent scenarios. An in-sample estimation of different copulas, using the GARCH models described in Sect. 5, is performed in order to find the best copula for each dataset. The likelihood value of each copula is compared within each dataset, using the Bayesian Information Criterion (BIC) to account for the number of parameters for each copula. The results are displayed in Table 7, and since the Student’s t-copula provides the best information for all datasets, we choose it to model the co-dependence across all models.

Table 7 BIC values for in-sample fitting of different copulas to different datasets

Now that we have described our scenario generation model, we take a step back to once again study the term structure volatility. We make the same analysis as in Fig. 4, but we use our simulation models to generate scenarios for each day and compute empirical volatilities for the in-sample period using 1000 scenarios for each day. The results are found in Fig. 8 and there is a striking similarity to the theoretical volatilities from the PCA. We clearly see that our way of modeling the evolution of term structures, in order to better fit the ex-post realizations, does not affect the volatility to a high degree. There is still a strong presence of noise in the Cubic spline models. In fact, very similar volatilities are obtained for the out-of-sample period as well. In Sect. 8 we will see how this affects the simulated volatilities and risk measures.

Fig. 8

Simulated in-sample term structure volatilities for our models compared to theoretical volatilities from the PCA seen as thin dashed lines

7 Back-testing and evaluation procedure

We now wish to evaluate which method is most consistent with the realizations that can be observed in the market during our out-of-sample period. Since we cannot directly observe term structures in the market, we compare it to the ones estimated using the different methods. The drawback of this approach is that it will make the realization, and thus this evaluation procedure, dependent on the term structure method used. Furthermore, it is problematic to evaluate time series of distributions of high dimensional term structures, against high dimensional realizations of term structures. Since term structures are primarily used to price interest rate instruments, we use portfolio values in order to reduce the dimensionality of the evaluation problem. By pricing a randomized portfolio using our generated term structure scenarios and comparing them to the historical realizations, we reduce the problem to evaluating distributions of portfolio values, compared to realized values. Besides evaluating the fit of the distribution, we will also study portfolio volatilities and VaR to get a grasp of the cost of using the different methods for measuring interest rate risk.

We use forward rate agreements (FRA) from the U.S. market to make up the portfolio as described earlier. Our portfolio tries to mimic an unhedged book by containing a randomized, normally distributed cash flow for each day. To be able to study interest rate risk over the entire maturity span up to 10 years, we use the market quoted FRA contracts up to 21 $\times$ 24 months, and in addition, we synthesize contracts for longer maturities spanning up to 117 $\times$ 120 months spaced with 3 months in between. We do this in order to capture the risk in the entire maturity span studied in Figs. 2, 3, 4, 5, 6, and 8. These figures highlight the problems to correctly estimate forward rate risk in Cubic spline term structures. We have set up trades to the quoted market rates when available, or the Blomvall (2017) forward rate, making the initial value of the synthetic contract close to zero. We keep only one single cashflow per day in order to minimize the amount of cashflows to handle when simulating over longer time periods, as described below. This is achieved by trading a normally distributed random amount in all maturities for all trading days during 3 months prior to the out-of-sample starting date. During the back-test, the longest contract is traded in order to maintain this structure. This results in a portfolio containing approximately 2500 instruments, which are constantly replaced as they roll out of maturity.

The back-testing system is built in C++, using a custom built portfolio management system for QuantLib (Ametrano and Ballabio 2000), which is scripted in Python. Since the portfolio for a given day is constant across all scenarios, the portfolio valuation procedure can be simplified. By gathering all cash flows from the instruments making up the portfolio into one composite instrument, and pricing this single instrument across all scenarios, a dramatic speed up is achieved. This makes it possible to simulate 2000 scenarios within approximately 2.5 s per model, using a standard desktop computer.

When simulation is carried out over a short time period, the LIBOR fixing rates observed in the market can be used for fixing the floating cash flows of the instruments. Over longer evaluations, these realized fixing rates will not match the generated term structure scenarios, as they should be a result of the realized path of the simulated term structures. For longer simulations, a trajectory of term structures for each trading day therefore has to be simulated. The fixing rate $r_f$ implied by a term structure for a given day $t_0$ can be calculated as

$$\begin{aligned} r_{t_0} = \frac{d(t_1) / d(t_2) - 1}{t}, \end{aligned}$$

(17)

where $d(t_1)$ is the discount factor for fixing date $t_1$ of $t_0$, $d(t_2)$ is the discount factor for the date resulting from advancing $t_1$ by the tenor period, and t is the time between $t_1$ and $t_2$, measured as a year fraction by the day-counting convention used in the market. When fixing rates differs among scenarios, portfolio composition will not only differ between days, but also between scenarios. This makes the valuation procedure substantially more computationally heavy.

7.1 Statistical test

In order to test different scenario generating models’ ability to generate scenarios that are consistent with historically observed realizations, we use a Wald-type test by Giacomini and White (2006). Consider the distribution function of the portfolio value $f_t(x)$, simulated over some time horizon starting at date t. Our goal should be to maximize the log-likelihood function of all n independent observations $x_t, t=1,\ldots ,n$,

$$\begin{aligned} \mathcal {L(\theta |{\mathbf {x}})} = \sum \limits _{t=1}^n \ln f_t(x_t) . \end{aligned}$$

(18)

The portfolios are identical across all models, but since the portfolio values are dependent on the term structure measurement method, our observations $x_t$, will differ among models.

Since we do not know the distribution function, only our simulated scenario values $x_{t,i}$ for $i=1,\ldots , s$, we will have to have to resort to a simulation-based maximum likelihood method. The method that we use is based on the method by Kristensen and Shin (2012), where they present a non-parametric kernel-based method to approximate the likelihood function. We introduce a kernel density function ${\hat{f}}_t(x)$, to approximate the real probability density function. Assume our s simulated portfolio scenario values of time t, follow the target distribution

$$\begin{aligned} x_{t,i}^\theta \sim f_t( \cdot | \theta ) . \end{aligned}$$

(19)

By the use of kernel-based methods, these scenarios can be used to estimate $f(x | \theta )$. Define the kernel density estimator

$$\begin{aligned} {\hat{f}}_t(x) = \frac{1}{n} \sum \limits _{k=1}^n K_h \left( x - x_t^\theta \right) , \end{aligned}$$

(20)

where

$$\begin{aligned} K_h(z) = \frac{K(z/h)}{h}. \end{aligned}$$

(21)

Here, $K( \cdot )$ is the kernel function, and $K_h$ is the scaled kernel function, where $h>0$ is the bandwidth. We use a Gaussian kernel given by

$$\begin{aligned} K_h(x - x_t^\theta ) = \frac{1}{\sqrt{2 \pi } h} \exp \left\{ \frac{-(x-x_t^\theta )^2}{2h^2} \right\} , \end{aligned}$$

(22)

which can be interpreted as placing a small Gaussian bell with standard deviation h, in each $x_t^\theta$. The kernel density estimator ${\hat{f}}(x)$ is given by the normed sum of these bells, or more formally

$$\begin{aligned} {\hat{f}}_t(x) = \frac{1}{\sqrt{2\pi } hs} \sum \limits _{i=1}^s \exp \left\{ \frac{-(x-x_{t,i}^\theta )^2}{2h^2} \right\} . \end{aligned}$$

(23)

It has been shown that if Gaussian kernel functions are used to approximate data where the underlying density is Gaussian, the optimal choice for the bandwidth is given by

$$\begin{aligned} h = \left( \frac{4\sigma ^5}{3s} \right) ^\frac{1}{5} , \end{aligned}$$

(24)

where $\sigma$ is the sample standard deviation of x (Silverman 1986).

Given the kernel density estimator in (23), we can replace the density function of from (18) by ${\hat{f}}(x_t)$ to get

$$\begin{aligned} \mathcal {L(\cdot |\theta )} = \sum \limits _{t=1}^n \ln {\hat{f}}_t(x_t) . \end{aligned}$$

(25)

By comparing these likelihood values, we can evaluate different models’ ability to measure risk. Using Pearson’s chi-squared test, we can examine whether the difference between the likelihood values of a reference model $\mathcal {L_R(\cdot |\theta )}$ and its comparison model $\mathcal {L_C(\cdot |\theta )}$ of two models are separated from zero. Define

$$\begin{aligned} \delta _t = \ln {\hat{f}}_t^R(x_t^R) - \ln {\hat{f}}_t^C(x_t^C), \quad \text {and} \quad {\bar{\delta }} = \frac{1}{n} \sum \limits _{t=1}^n \delta _t , \end{aligned}$$

(26)

which gives us the test statistic

$$\begin{aligned} \frac{n^2 {\bar{\delta }}^2}{ \sum \nolimits _{t=1}^n \delta _t^2} \sim \chi ^2(1) . \end{aligned}$$

(27)

Besides the statistical test, the kernel distribution can be used for computing VaR or expected shortfall numerically.

8 Simulation results

In order to generate term structure scenarios that are consistent with historical observations, the univariate distribution of the changes in each risk factor have to be accurate, even for the out-of-sample data. However, as explained in Sect. 6, consistent univariate distributions do not guarantee that the scenarios are consistent in the case of co-dependence. Since it is necessary to match the univariate distributions, we start by showing out-of-sample QQ-plots for the three most significant risk factors for our GJR-GARCH model, using the Blomvall (2017) data. The results shown in Fig. 9 are promising, and superior compared to similar results of constant volatility models, which we saw perform poorly even for the in-sample period (Fig. 7). We thus turn to the back-test described in Sect. 7 using this model with the Student’s t-copula.

Fig. 9

Out-of-sample QQ-plot of forecasted normalized residuals of principal component innovations for the Blomvall (2017) model, fitted 1999–2006 displaying 4 years between 2006 and 2010, thus including the financial crisis

8.1 Back-test using a 1-day forecasting horizon

We compare our datasets, using the portfolio which values we presented in Fig. 1 earlier. In order to emphasize the fact that the choice of forward rates or spot rates have very limited impact of the results of the Blomvall (2017) model, as indicated by the term structure volatility displayed in Fig. 8, we also provide results using spot rate risk factors. We also provide the results of a Cubic spline model using a constant volatility, normally distributed residuals with an independence copula. This represents independent scenario simulation using the results from the PCA on spot rate innovations directly, which would be a basic model requiring minimal implementation. The distribution of scenario volatilities, together the overall portfolio volatility is shown in Fig. 10. Here we have capped the simulation volatilitiy values at 100, in order to avoid unrealistic scenario outcomes, causing misrepresentation of the sample volatilities ${\bar{\sigma }}$. In order to be able to compare the scenario volatilities to the portfolio volatilities in Table 1, we compute them as the standard deviation with the portfolio value from the previous day as the sample mean. We note that the capped simulated volatilities in Fig. 10 are very close to the portfolio volatilities presented in Table 1, and that the Blomvall (2017) models produce the lowest scenario volatilities followed by the Nelson and Siegel (1987) model. We also note that the Cubic spline model attains a lower portfolio volatility when spot rate risk factors are used compared to forward rate risk factors, which is expected according to Fig. 8, where the spot rate volatilities are lower. Low scenario volatility implies lower risk measures, which is desirable as long as the risk measure is consistent with realized outcomes, and the model produces prices that are consistent with market prices, without systematic errors. Systematic price errors were investigated in Sect. 2, and consistency with realized outcomes will now be studied using histograms together with the statistical test from Sect. 7.1.

Fig. 10

Histogram of the out-of-sample 1-day-ahead scenario volatilities between 2002 and 2017 for the portfolio. Values are capped at 100

Using the kernel to obtain a continuous distribution, we use its inverse distribution to retrieve supposedly uniformly distributed random variables. From the inversion principle we know that these random variables will be uniformly distributed if the scenarios give a correct description of the realized portfolio returns. We study this using histograms, and the result over the out-of-sample period is shown in Fig. 11. We note that the Blomvall (2017) model display a good fit relative to the realizations. Other models generally overestimate the risk in most cases, as indicated by higher probability mass in the center of the distribution. This is the result of most realizations having a smaller magnitude than the model predicts. However, all the Cubic spline models underestimate the risk for the most extreme realizations, as indicated by the higher bars in the tails of the distribution.

Fig. 11

Out-of-sample results between 2002 and 2017 using zero mean, GJR-GARCH and Student’s t-copula except for the last model which has constant volatility model with an independence copula

Applying the statistical test from Sect. 7.1, we get the results displayed in Table 8. The Blomvall (2017) model obtain significantly higher likelihood values than the spline models. The Nelson and Siegel (1987) model obtain a higher likelihood value, but this is not statistically significant. Two of the Cubic spline models provide outliers that are so unlikely that their probability is equal to zero. This results in numerical problems, but we can interpret this as $p=0$. The Cubic spline model based on spot rate risk factors exhibits a better fit in the histogram and in the statistical test. In addition, it produces lower portfolio volatility as seen earlier.

Table 8 Results for the 1-day-horizon, where ${\bar{\delta }}$ is the difference in likelihood value between the Blomvall (2017) model and the compared model

Even though we model the entire distribution, we can use the scenarios and the kernel function to study the left tail of the distribution to compute VaR. We study this by sorting the supposedly uniformly distributed values that we retrieve from transforming realized portfolio values by the inverse of the kernel function. In the left panel of Fig. 12 we can depict the ex-post realizations of how often extreme losses occur relative to the expected frequency. We also use the kernel distribution to numerically compute ex-ante estimations of VaR for different confidence levels, shown in the right panel of Fig. 12. We see that the Blomvall (2017) models produce the lowest VaR levels while having a very accurate representation of the tail distribution (left panel). Here, we also confirm that all the Cubic spline models underestimate the extreme tail risk, as previously seen in the histograms in Fig. 11. This causes the constant volatility Cubic spline model to falsely perceive a relatively flat VaR curve for increasing confidence levels (right panel). Our Cubic spline model based on spot rate risk factors exhibits a lower VaR curve, as would be expected with the lower volatility results of Fig. 10. However, a part of this result comes at the price of underestimating the risk across all confidence levels displayed in the left panel of Fig. 12. The Nelson and Siegel (1987) model overestimates the risk but still produces lower risk estimates compared to the Cubic spline models. Even though we only calculate VaR, the results are translated to expected shortfall as this is the expectation of VaR below the quantile.

Fig. 12

Tail risk QQ and 1-day-ahead average VaR over the out-of-sample period

8.2 Back-test using a 10-day forecasting horizon

We also provide results for a 10-day horizon, since this is commonly used in Basel regulations. For this horizon, we start to notice differences between the analytical and the simulation based approach described in Sect. 5.1, and we thus use the simulation based approach with 2000 scenarios. We chose to concentrate on the models displaying the best results for the 1-day simulation based on the amount of volatility and statistical test. Hence, we chose the Cubic spline model using spot rate risk factors, together with the Nelson and Siegel (1987) model as reference models. The scenario volatilities is shown in Fig. 13. Here we have capped simulation volatilitiy values at 150, due to unrealistic scenario outcomes, which mainly affects the Nelson and Siegel (1987) model, in terms of decreased average volatility.

Fig. 13

Histogram of the out-of-sample 10-day scenario volatilities between 2002 and 2017 for the portfolio. Values are capped at 150

Fig. 14

Out-of-sample results for a 10-day horizon plotted against the uniform distribution

Table 9 Results for the 10-day simulation horizon, where ${\bar{\delta }}$ is the difference in likelihood value between the reference model and the Blomvall (2017) model

Fig. 15

Tail risk QQ and 1-day-ahead median values for VaR over the out-of-sample period

Studying the fit of our models in Fig. 14 we start to notice a slight overestimation of the risk in the Blomvall (2017) model and the Nelson and Siegel (1987) model, especially for positive returns. The Cubic spline model displays a more severe overestimation of the risk. Turning once again to the statistical test, we ran a separate test where simulations were spaced equal to the simulation horizon of 10 days to ensure that there is no dependence between observations, as required by the test. The results can be seen in Table 9, where we find that the model by Blomvall (2017) produces significantly higher likelihood values than both the Cubic spline model and the dynamic Nelson and Siegel (1987) model.

Studying the VaR for this commonly used simulation horizon, seen in Fig. 15, we note that the tail risk is overestimated by all models at this simulation horizon. Due to some unrealistic scenario values of the Nelson and Siegel (1987), we have use median values instead of average values of VaR. These measures are substantially lower for the Blomvall (2017) model, especially for the lowest percentile. This is a result of the model generating excessive noise in addition to the actual risk, something that would unnecessarily increase capital requirements under Basel regulations.

8.3 Long-term back-testing

As pointed out by Rebonato et al. (2005), evolving yield curves over long horizons is a difficult task, and as described earlier, long-term scenario simulation using daily forecasts is a computationally cumbersome process. Because of this, we have limited the test to a one-quarter-ahead simulation using 500 scenarios. We perform weekly simulations instead of daily in order for the model to finish within 12 h. The volatility distribution is presented in Fig. 16. Here we have capped volatility values at 250, due to highly unrealistic scenario values. This mainly affects the Nelson and Siegel (1987) model, but also the Cubic spline model, while the Blomvall (2017) model shows no signs of unrealistic scenarios.

Fig. 16

Histogram of the weekly out-of-sample one-quarter-ahead scenario volatilities between 2002 and 2017 for the portfolio. Values are capped at 500

Studying the histogram in Fig. 17 we note that the Blomvall (2017) has the best fit, while other models show more severe problems even though the fit for positive returns is a recurring problem for all models. We perform no statistical test for this horizon due to the limited number of independent observations. Computing the VaR measures in Fig. 18 has to be done using median value instead of average due to the unrealistic scenarios mentioned above. All models overestimate the risk, but the Blomvall (2017) model shows the best fit and provides substantially lower VaR measures.

Fig. 17

Weekly Out-of-sample results between with simulation horizon of one quarter

Fig. 18

Tail risk QQ and one-quarter-ahead median VaR for the out-of-sample period

8.4 Towards accurate measurements of interest rate risk

To accurately model interest rate risk, it is necessary to ensure that the model does not capture noise. It is evident from the right panel of Fig. 4 that, measuring interest rate curves using cubic splines, introduces noise that may be hidden in the PCA of spot rates. Even though adding more realistic modeling of the principal components for the Cubic spline models significantly improves the results (Figs. 11, 12), it is obvious that improved modeling will not overcome the fact that noise is being modeled. As a direct consequence, the Cubic spline models manage to overestimate the inherent interest rate risk ex-ante, while it simultaneously underestimates the tail risk ex-post for the daily horizon (Fig. 12). The inherent property that Cubic spline models cannot deal with measurement noise that creates unrealistic interest rates for the 10-day and quarterly simulation horizons. The consequence of this is very high VaR measures (Figs. 15, 18).

The Nelson and Siegel (1987) model creates less accurate prices (Fig. 1), but simultaneously improve the risk measurement both ex-ante and ex-post compared to the Cubic spline models (Fig. 12). However, for longer horizons, also the Nelson and Siegel (1987) model tend to increase the risk significantly (Figs. 15, 18), indicating that this model also models noise to a large extent. Relying on a formulation of the inverse problem that is more resilient to measurement noise, as the one suggested by Blomvall (2017), allows for decreased VaR and expected shortfall measures. This results in lower capital requirements for the FRTB, while having control over the realized risk.

9 Conclusions

This paper concerns modeling of the entire distribution of interest rate risk by modeling its systematic risk factors. We find GARCH-models useful for modeling of the volatility of principal component series. We also find that the Student’s t-copula is the most suitable copula for modeling co-dependence between these principal component series. Based on these findings, we construct models that are independent of the underlying term structure measurement methods and work in all regimes, including negative interest rates. After establishing the interconnection between the measurement of interest rate risk, and the measurement of term structures, we identify three important properties. First, there should be no systematic price errors caused by the term structure measurement method. Second, the distribution of the risk factors must be consistent with their realizations. Third, lower risk is preferable. We investigate these three properties and seek a model which satisfies them all. Scenario volatility of different models are studied in order to compare their level of risk. The ability to generate scenarios that are consistent with realized outcomes, is studied by valuing a portfolio containing interest rate derivatives, and compare scenario values with realized outcomes. In order to reveal any weakness of the model, we choose forward rate agreements to make up the portfolio. These instruments are sensitive to changes to the forward rates, which is an inherent problem for traditional interest rate measurement methods. We conclude that our proposed model, based on Blomvall (2017) term structures, accurately reflects 1-day-ahead the risk in in the portfolio, while obtaining the lowest volatility and VaR levels. For the 10-day horizon, Cubic spline models and the Nelson and Siegel (1987) model exhibit further problems caused by the volatility arising from noise being scaled by the increased time horizon, leading to unnecessarily increases in capital requirements under Basel regulations. For long-term simulations over a quarter, the Blomvall (2017) produces the by far best results. We conclude that the term structures by the Blomvall (2017) model contain the least amount of noise, but that the method could be improved in order to further reduce the amount of noise. We believe that this would further reduce the measured risk, as well as improve the fit of the risk distribution for longer simulation horizons.