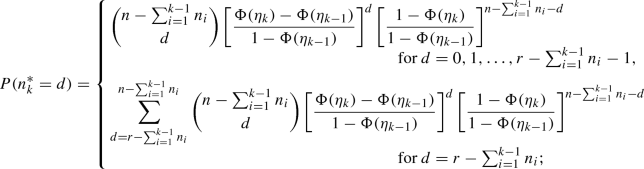Abstract
The optimal design of a k-level step-stress accelerated life-testing (ALT) experiment with unequal duration steps under Type-I hybrid censoring scheme for a general log-location-scale lifetime distribution is discussed here. Censoring is allowed only at the change-stress point in the final stage. Based on the cumulative exposure model, the determination of the optimal choice for Weibull, lognormal and log-logistic lifetime distributions are considered by minimization of the asymptotic variance of the maximum likelihood estimate of the pth percentile of the lifetime at the normal operating condition. Numerical results show that for these lifetime distributions, the optimal k-step-stress ALT design with unequal duration steps under Type-I hybrid censoring scheme reduces just to a 2-step-stress ALT design.
Similar content being viewed by others
References
Alhadeed AA, Yang SS (2005) Optimal simple step-stress plan for cumulative exposure model using log-normal distribution. IEEE Trans Reliab 54:64–68
Bai DS, Kim MS (1993) Optimum simple step-stress accelerated life tests for Weibull distribution and Type I censoring. Naval Res Logist 40:193–210
Bai DS, Kim MS, Lee SH (1989) Optimum simple step-stress accelerated life test with censoring. IEEE Trans Reliab 38:528–532
Balakrishnan N (2009) A synthesis of exact inferential results for exponential step-stress models and associated optimal accelerated life-tests. Metrika 69:351–396
Balakrishnan N, Han D (2009) Optimal step-stress testing for progressively Type-I censored data from exponential distribution. J Stat Plan Inference 139:1782–1798
Balakrishnan N, Kundu D (2013) Hybrid censoring: models, inferential results and applications. Comput Stat Data Anal 57:166–209 (with discussions)
Balakrishnan N, Xie Q (2007) Exact inference for a simple step-stress model with Type-I hybrid censored data from the exponential distribution. J Stat Plan Inference 137:3268–3290
Balakrishnan N, Zhang L, Xie Q (2009) Inference for a simple step-stress model with Type-I censoring and lognormally distributed lifetimes. Commun Stat Theory Methods 38:1690–1709
Chung SW, Bai DS (1998) Optimal designs of simple step-stress accelerated life tests for lognormal lifetime distributions. Int J Reliab Qual Saf Eng 5:315–336
Chung SW, Seo YS, Yun WY (2006) Acceptance sampling plans based on failure-censored step-stress accelerated tests for Weibull distributions. J Qual Maint Eng 12:373–396
Corana A, Marchesi M, Martini C, Ridella S (1987) Minimizing multi-modal functions of continuous variables with the “simulated annealing” algorithm. ACM Trans Math Softw 13:262–280
Dharmadhikari AD, Rahman MM (2003) A model for step-stress accelerated life testing. Naval Res Logist 50:841–868
Ding C, Yang C, Tse S-K (2010) Accelerated life test sampling plans for the Weibull distribution under Type I progressive interval censoring with random removals. J Stat Comput Simul 80:903–914
Fard N, Li C (2009) Optimal simple step stress accelerated life test design for reliability prediction. J Stat Plan Inference 139:1799–1808
Gouno E, Sen A, Balakrishnan N (2004) Optimal step-stress test under progressive Type-I censoring. IEEE Trans Reliab 53:383–393
Han D, Balakrishnan N, Sen A, Gouno E (2006) Corrections on “Optimal step-stress test under progressive Type-I censoring”. IEEE Trans Reliab 55:613–614
Jones MC, Noufaily A (2015) Log-location-scale-log-concave distributions for survival and reliability analysis. Electron J Stat 9:2732–2750
Kateri M, Balakrishnan N (2008) Inference for a simple step-stress model with Type-II censoring, and Weibull distributed lifetimes. IEEE Trans Reliab 57:616–626
Khamis IH (1997) Optimum \(m\)-step, step-stress design with \(k\) stress variables. Commun Stat Simul Comput 26:1301–1313
Khamis IH, Higgins JJ (1996) Optimum 3-step step-stress tests. IEEE Trans Reliab 45:341–345
Kiefer J (1974) General equivalence theory for optimum designs (approximate theory). Ann Stat 2:849–879
Lin CT, Chou CC, Balakrishnan N (2013) Planning step-stress test plans under Type-I censoring for the log-location-scale case. J Stat Comput Simul 83:1852–1867
Lin CT, Chou CC, Balakrishnan N (2014) Planning step-stress test under Type-I censoring for the exponential case. J Stat Comput Simul 84:819–832
Lin CT, Huang YL, Balakrishnan N (2011) Exact Bayesian variable sampling plans for the exponential distribution with progressive hybrid censoring. J Stat Comput Simul 81:873–882
Ling L, Xu W, Li M (2011) Optimal bivariate step-stress accelerated life test for Type-I hybrid censored data. J Stat Comput Simul 81:1175–1186
Ma H, Meeker WQ (2008) Optimum step-stress accelerated life test plans for log-location-scale distributions. Naval Res Logist 55:551–562
Miller R, Nelson WB (1983) Optimum simple step-stress plans for accelerated life testing. IEEE Trans Reliab 32:59–65
Nelson WB (1990) Accelerated testing: statistical models, test plans, and data analysis. Wiley, New York
Nelson WB (2005a) A bibliography of accelerated test plans, part I-overview. IEEE Trans Reliab 54:194–197
Nelson WB (2005b) A bibliography of accelerated test plans, part II-references. IEEE Trans Reliab 54:370–373
Nelson WB, Kielpinski TJ (1976) Theory for optimum censored accelerated life tests for normal and lognormal life distributions. Technometrics 18:105–114
Srivastava PW, Shukla R (2008) A log-logistic step-stress model. IEEE Trans Reliab 57:431–434
Tang LC, Sun YS, Goh TN, Ong HL (1996) Analysis of step-stress accelerated-life-test data: a new approach. IEEE Trans Reliab 45:69–74
Wu SJ, Lin YP, Chen YJ (2006) Planning step-stress life test with progressively Type-I group-censored exponential data. Stat Neerl 60:46–56
Wu SJ, Lin YP, Chen ST (2008) Optimal step-stress test under Type-I progressive group-censoring with random removals. J Stat Plan Inference 138:817–826
Yeo KP, Tang LC (1999) Planning step-stress life-test with a target acceleration-factor. IEEE Trans Reliab 54:370–373
Acknowledgements
The authors express their sincere thanks to the Editor, Associate Editor, and an anonymous reviewer for their valuable comments and suggestions on an earlier version of this manuscript which led to this improved version. The first author thanks the Ministry of Science and Technology of the Republic of China, Taiwan (Contract No: MOST 106-2118-M-032-006-MY2) for funding this research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
For deriving the entries of the Fisher information matrix, we need the following properties concerning the count variables and order statistics.
Some important properties
- (a)
The random variable \(n_1\) has a binomial distribution with parameters \((n, \Phi (\eta _1))\). For \(i=2, 3, \ldots , k-1\), given \(n_1, n_2, \ldots , n_{i-1}\), the random variable \(n_i\) has a binomial distribution with parameters \( \displaystyle \left( n-\sum _{j=1}^{i-1} n_j, \frac{\Phi (\eta _i)-\Phi (\eta _{i-1})}{1- \Phi (\eta _{i-1})} \right) \); here,
$$\begin{aligned} \eta _i=\frac{\ln (\tau _i+ s_{i-1}- \tau _{i-1})- (\beta _0+ \beta _1 x_i)}{\sigma }, \quad i=1, 2, \ldots , k, \ \eta _0 \equiv -\infty ; \end{aligned}$$(4) - (b)
Given \(n_1, n_2, \ldots , n_{k-1}\), the random variable \(n_k^*\) has probability mass function
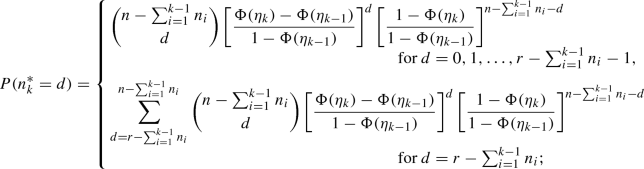
- (c)
Given \(n_1, n_2, \ldots , n_i\), the random variables \(y_{i,j}\), \(j=1, 2, \ldots , n_i\), are distributed jointly as order statistics from a random sample of size \(n_i\) from a doubly truncated population with PDF \( \displaystyle \frac{g_i(y)}{\Phi (\eta _{i})-\Phi (\eta _{i-1})}\) for \( \tau _{i-1} \le y \le \tau _i\) and \(i=1, 2, \ldots , k-1\), where \(g_i(\cdot )\) is as defined earlier in (2);
- (d)
Given \(n_1, n_2, \ldots , n_{k-1}\), the random variables \(y_{k,j}\), \(j=1, 2, \ldots , n_k^*\), are distributed jointly as order statistics from a random sample of size \(n_k^*\) from a doubly truncated population with PDF \(\displaystyle \frac{g_k(y)}{\Phi (\eta _{k})-\Phi (\eta _{k-1})}\) for \(\tau _{k-1} < y \le \tau _k\).
Using the above key distributional properties, we obtain
for \(q=0, 1, 2, \ell =0, 1, 2\), and \(i=1, \ldots , k\), where
For \(q=0, 1, 2\), \(\ell =0, 1, 2\), and \(h=0,1\), we define
We then have
and
and
Hence, the entries of the Fisher information matrix are as follows:
Rights and permissions
About this article
Cite this article
Lin, CT., Chou, CC. & Balakrishnan, N. Planning step-stress test plans under Type-I hybrid censoring for the log-location-scale distribution. Stat Methods Appl 29, 265–288 (2020). https://doi.org/10.1007/s10260-019-00476-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-019-00476-8