Abstract
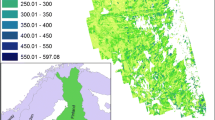
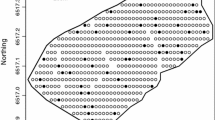
A coherent set of explicit approximations is presented for the variance of planar area and volume estimators obtained under systematic geometric sampling. For planar objects (e.g. a land plot, or a tissue section), sampling is considered with test systems of points, lines, segments, stripes, or quadrats. For three dimensional objects analogous probes are considered. For the formulae to apply the design has to be uniform random (which suffices to estimate planar area or volume only) and also isotropic. The formulae are based on G. Matheron’s transitive theory. A synthetic example on the estimation of canopy cover is explained in detail.
Similar content being viewed by others
References
Abramowitz M, Stegun IA (1965) Handbook of mathematical functions. Dover, New York
Baddeley AJ, Jensen EBV (2005) Stereology for statisticians. Chapman&Hall/CRC, London
Barabesi L, Fattorini L (1998) The use of replicated plot, line and point sampling for estimating species abundance and ecological diversity. Environ Ecol Stat 5: 353–370
Barabesi L, Marcheselli M (2008) Improved strategies for coverage estimation by using replicated line-intercept sampling. Environ Ecol Stat 15: 215–239
Cochran WG (1977) Sampling techniques. 3rd edn. Wiley & Sons., New York
Cruz-Orive LM (1989) On the precision of systematic sampling: a review of Matheron’s transitive methods. J Microsc 153: 315–333
Cruz-Orive LM (1993) Systematic sampling in stereology. Bull Int Stat Inst Proc 49th Session, Florence 1993 55(2): 451–468
Cruz-Orive LM (1997) Stereology of single objects. J Microsc 186: 93–107
Cruz-Orive LM (2002) Stereology: meeting point of integral geometry, probability, and statistics. In memory of Professor Luis A. Santaló (1911–2001). Special issue (Homenaje a Santaló) of Mathematicae Notae 41:49-98
Cruz-Orive LM (2006) A general variance predictor for Cavalieri slices. J Microsc 222: 158–165
Cruz-Orive LM et al (2009) Stereology: old and new. In: Capasso V. (ed) Proceedings of the 10th European Congress of ISS. The MIRIAM Project Series. ESCULAPIO Pub.Co., Bologna, pp 1–12
Cruz-Orive LM, Ramos-Herrera ML, Artacho-Pérula E (2010) Stereology of isolated objects with the invariator. J Microsc 240: 94–110
García-Fiñana M (2006) Confidence intervals in Cavalieri sampling. J Microsc 222: 146–157
García-Fiñana M, Cruz-Orive LM (2004) Improved variance prediction for systematic sampling on \({\mathbb{R}}\). Statistics 38: 243–272
Gual-Arnau X, Cruz-Orive LM (1998) Variance prediction under systematic sampling with geometric probes. Adv Appl Probab 30: 889–903
Guelfand IM, Chilov GE (1962) Les distributions. Tome 1. Dunod, Paris
Gundersen HJG, Jensen EB (1987) The efficiency of systematic sampling in stereology and its prediction. J Microsc 147: 229–263
Howard CV, Reed MG (2005) Unbiased stereology. Three-dimensional measurement in microscopy. 2nd edn. Bios/Taylor&Francis, Oxford
Kendall MG, Moran PAP (1963) Geometrical probability. Ch.Griffin, London
Kiêu K, Mora M (2006) Precision of stereological planar area predictors. J Microsc 222: 201–211
Kiêu K, Souchet S, J Istas (1999) Pre cision of systematic sampling and transitive methods. J Stat Plan Inf 77: 263–279
Korhonen L, Korhonen KT, Rautianen M, Stenberg P (2006) Estimation of forest canopy cover: a comparison of field measurement echniques. Silva Fennica 40: 577–588
Kubínová L, Janác̆ek J (2001) Confocal microscopy and stereology: estimating volume, number, surface area and length by virtual test probes applied to three-dimensional images. Microsc Res Technol 53: 425–435acute;
Matérn B (1985) Estimating area by dot counts. Contributions to Probability and Statistics. In Honour of Gunnar Blom, (ed. by J. Lanke and G. Lindgren), pp. 243–257. Department of Mathematical Statistics, Lund
Matérn B (1989) Precision of area estimation: a numerical study. J Microsc 153: 269–284
Matheron G (1965) Les Variables Régionalisées et Leur Estimation. Masson et Cie., Paris
Matheron G (1971) The theory of regionalized variables and its applications. Les Cahiers du Centre de Morphologie Mathématique de Fontainebleau, No. 5, école Nationale Supérieure des Mines de Paris, Fontainebleau
Moran PAP (1950) Numerical integration by systematic sampling. Proc Camb Phil Soc 46: 111–115
Santaló LA (1976) Integral geometry and geometric probability. Addison-Wesley, Reading
Schneider R, Weil W (2008) Stochastic and integral geometry. Springer, Berlin
Souchet S (1995) Précision de l’estimateur de Cavalieri. Rapport de stage, D.E.A. de Statistiques et Modèles Aleatoires appliqués a la Finance, Université Paris-VII, Laboratoire de Biométrie, INRA-Versailles
Voss F, Cruz-Orive LM (2009) Second moment formulae for geometric sampling with test probes. Statistics 43: 329–365
Weibel ER (1979) Stereological methods. Vol. 1: Practical methods for biological morphometry. Academic Press, London
Wulfsohn D, Sciortino M, Aaslyng JM, García-Fiñana M (2010) Non-destructive, stereological estimation of canopy surface area. Biometrics 66: 159–168
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cruz-Orive, L.M. Variance predictors for isotropic geometric sampling, with applications in forestry. Stat Methods Appl 22, 3–31 (2013). https://doi.org/10.1007/s10260-012-0211-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-012-0211-6