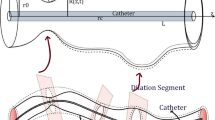
Abstract
Obstruction of left anterior descending artery (LAD) due to the thrombosis or atherosclerotic plaques is the leading cause of death worldwide. Targeted delivery of drugs through micro- and nanoparticles is a very promising approach for developing new strategies in clot-busting or treating restenosis. In this work, we modelled the blood flow characteristics in a patient-specific reconstructed LAD artery by the fluid–solid interaction method and based on physiological boundary conditions. Next, we provided a Lagrangian description of micro- and nanoparticles dynamics in the blood flow considering their Brownian motion and the particle–particle interactions. Our results state that the number of spherical particles migrating towards the region of lumen with potential of thrombus existence (PTE) rises by increasing the particle size. Also, an optimum scope of particle size in which the adhesive probability parameter reaches its maximum was determined. We acquired an optimum scope for a specific degree of particle sphericity in which the thrombus surfaces experience the maximum density of interaction with particles. We learned that the ligand–receptor mechanism-based drug carriers are better choices for treating LAD arterial diseases when the addressees are patients with low haematocrit-related diseases. While due to the amount of shear stress exerting on the diseased area, generally exploiting nanoshear-activated drug carriers would be the more effective option when it comes to the thrombolytic therapies of patients with high haematocrit-related diseases.
















Similar content being viewed by others
References
Abba AA, Wani BA, Rahmatullah RA, Khalil MZ, Kumo AM, Ghonaim MA (2003) Door to needle time in administering thrombolytic therapy for acute myocardial infarction. Saudi Med J 24(4):361–4
Abeddoust M, Shamloo A (2015) A model for cell density effect on stress fiber alignment and collective directional migration. Phys Biol 12(6):066023
Ali MR, Salim Hossain M, Islam MA, Saiful Islam Arman M, Sarwar Raju G, Dasgupta P, Noshin TF (2014) Aspect of thrombolytic therapy: a review. Sci World J 2014:586510
Bächer C, Schrack L, Gekle S (2017) Clustering of microscopic particles in constricted blood flow. Phys Rev Fluids 2(1):013102
Bagge U, Karlsson R (1980) Maintenance of white blood cell margination at the passage through small venular junctions. Microvasc Res 20(1):92–95
Boutsianis E, Dave H, Frauenfelder T, Poulikakos D, Wildermuth S, Turina M, Ventikos Y, Zund G (2004) Computational simulation of intracoronary flow based on real coronary geometry. Eur J Cardiothorac Surg 26(2):248–56
Carboni E, Tschudi K, Nam J, Lu X, Ma AW (2014) Particle margination and its implications on intravenous anticancer drug delivery. AAPS PharmSciTech 15(3):762–71
Colwell JA, Lopes-Virella M, Halushka PV (1981) Pathogenesis of atherosclerosis in diabetes mellitus. Diabetes Care 4(1):121–33
Dasgupta S, Auth T, Gompper G (2013) Wrapping of ellipsoidal nano-particles by fluid membranes. Soft Matter 9:5473–5482
Debakey ME, Lawrie GM, Glaeser DH (1985) Patterns of atherosclerosis and their surgical significance. Ann Surg 201(2):115–131
Decuzzi P, Ferrari M (2006) The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 27(30):5307–14
Decuzzi P, Pasqualini R, Arap W, Ferrari M (2009) Intravascular delivery of particulate systems: does geometry really matter? Pharm Res 26(1):235–43
Eckstein EC, Tilles AW, Millero FJ 3rd (1988) Conditions for the occurrence of large near-wall excesses of small particles during blood flow. Microvasc Res 36(1):31–9
El-Sherbiny IM, Elkholi IE, Yacoub MH (2014) Tissue plasminogen activator-based clot busting: controlled delivery approaches. Glob Cardiol Sci Pract 2014(3):336–49
Fedosov DA (2010) Multiscale modeling of blood flow and soft matter. Brown University, Providence
Fournier RL (2011) Basic transport phenomena in biomedical engineering, 3rd edn. Taylor & Francis, Philadelphia
Gentile F, Chiappini C, Fine D, Bhavane RC, Peluccio MS, Cheng MM, Liu X, Ferrari M, Decuzzi P (2008) The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows. J Biomech 41(10):2312–8
Glagov S, Weisenberg E, Zarins CK, Stankunavicius R, Kolettis GJ (1987) Compensatory enlargement of human atherosclerotic coronary arteries. N Engl J Med 316(22):1371–1375
Godin B, Driessen WHP, Proneth B, Lee S-Y, Srinivasan S, Rumbaut R, Arap W, Pasqualini R, Ferrari M, Decuzzi P (2010) An integrated approach for the rational design of nanovectors for biomedical imaging and therapy. Adv Genet 69:31–64
Goldman AJ, Cox RG, Brenner H (1967) Slow viscous motion of a sphere parallel to a plane wall–II Couette flow. Chem Eng Sci 22(4):653–660
Goldsmith HL, Spain S (1984) Margination of leukocytes in blood flow through small tubes. Microvasc Res 27(2):204–222
Gradus-Pizlo I, Bigelow B, Mahomed Y, Sawada SG, Rieger K, Feigenbaum H (2003) Left anterior descending coronary artery wall thickness measured by high-frequency transthoracic and epicardial echocardiography includes adventitia. Am J Cardiol 91(1):27–32
Grief AD, Richardson G (2005) Mathematical modelling of magnetically targeted drug delivery. J Magn Magn Mater 293(1):455–463
Haverkort JW, Kenjereš S, Kleijn CR (2009) Computational simulations of magnetic particle capture in arterial flows. Ann Biomed Eng 37(12):2436–2448
Johnston BM, Johnston PR, Corney S, Kilpatrick D (2004) Non-Newtonian blood flow in human right coronary arteries: steady state simulations. J Biomech 37(5):709–20
Karimi A, Navidbakhsh M, Faghihi S, Shojaei A, Hassani K (2013) A finite element investigation on plaque vulnerability in realistic healthy and atherosclerotic human coronary arteries. Proc Inst Mech Eng H 227(2):148–61
Karimi A, Navidbakhsh M, Shojaei A, Hassani K, Faghihi S (2014) Study of plaque vulnerability in coronary artery using Mooney–Rivlin model: a combination of finite element and experimental method. Biomed Eng Appl Basis Commun 26(01):1450013
Kenjereš S, Righolt BW (2012) Simulations of magnetic capturing of drug carriers in the brain vascular system. Int J Heat Fluid Flow 35:68–75
Kim M (2004) Effect of electrostatic, hydrodynamic, and Brownian forces on particle trajectories and sieving in normal flow filtration. J Colloid Interface Sci 269(2):425–431
Kim HJ, Vignon-Clementel IE, Coogan JS, Figueroa CA, Jansen KE, Taylor CA (2010) Patient-specific modeling of blood flow and pressure in human coronary arteries. Ann Biomed Eng 38(10):3195–209
Kimmel SE, Berlin JA, Hennessy S, Strom BL, Krone RJ, Laskey WK (1997) Risk of major complications from coronary angioplasty performed immediately after diagnostic coronary angiography: results from the Registry of the Society for Cardiac Angiography and Interventions. J Am Coll Cardiol 30(1):193–200
Kirby BJ (2010) Micro- and nanoscale fluid mechanics: transport in microfluidic devices. Cambridge University Press, New York
Korin N, Kanapathipillai M, Matthews BD, Crescente M, Brill A, Mammoto T, Ghosh K, Jurek S, Bencherif SA, Bhatta D, Coskun AU, Feldman CL, Wagner DD, Ingber DE (2012) Shear-activated nanotherapeutics for drug targeting to obstructed blood vessels. Science 337(6095):738–42
Kwon O, Krishnamoorthy M, Cho YI, Sankovic JM, Banerjee RK (2008) Effect of blood viscosity on oxygen transport in residual stenosed artery following angioplasty. J Biomech Eng 130(1):011003
Lee J, Smith NP (2012) The multi-scale modelling of coronary blood flow. Ann Biomed Eng 40(11):2399–413
Lee SY, Ferrari M, Decuzzi P (2009) Design of bio-mimetic particles with enhanced vascular interaction. J Biomech 42(12):1885–90
Letcher RL, Chien S, Pickering TG, Laragh JH (1983) Elevated blood viscosity in patients with borderline essential hypertension. Hypertension 5(5):757–62
Li A, Ahmadi G (1992) Dispersion and deposition of spherical particles from point sources in a turbulent channel flow. Aerosol Sci Technol 16(4):209–226
Lowe GD (1986) Blood rheology in arterial disease. Clin Sci (Lond) 71(2):137–46
Mody NA, King MR (2007) Influence of Brownian motion on blood platelet flow behavior and adhesive dynamics near a planar wall. Langmuir 23(11):6321–8
Muller K, Fedosov DA, Gompper G (2014) Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Sci Rep 4:4871
Muller K, Fedosov DA, Gompper G (2016) Understanding particle margination in blood flow—a step toward optimized drug delivery systems. Med Eng Phys 38(1):2–10
Multiphysics C (2015) Particle tracing module user’s guide, COMSOL
Nacev A, Beni C, Bruno O, Shapiro B (2011) The behaviors of ferro-magnetic nano-particles in and around blood vessels under applied magnetic fields. J Magn Magn Mater 323(6):651–668
Namdee K, Thompson AJ, Charoenphol P, Eniola-Adefeso O (2013) Margination propensity of vascular-targeted spheres from blood flow in a microfluidic model of human microvessels. Langmuir 29(8):2530–5
Namdee K, Thompson AJ, Golinski A, Mocherla S, Bouis D, Eniola-Adefeso O (2014) In vivo evaluation of vascular-targeted spheroidal microparticles for imaging and drug delivery application in atherosclerosis. Atherosclerosis 237(1):279–86
Pries AR, Neuhaus D, Gaehtgens P (1992) Blood viscosity in tube flow: dependence on diameter and hematocrit. Am J Physiol 263(6 Pt 2):H1770–8
Sarnak MJ, Tighiouart H, Manjunath G, MacLeod B, Griffith J, Salem D, Levey AS (2002) Anemia as a risk factor for cardiovascular disease in The Atherosclerosis Risk in Communities (ARIC) study. J Am Coll Cardiol 40(1):27–33
Schuhlen H, Kastrati A, Dirschinger J, Hausleiter J, Elezi S, Wehinger A, Pache J, Hadamitzky M, Schomig A (1998) Intracoronary stenting and risk for major adverse cardiac events during the first month. Circulation 98(2):104–11
Serda RE (2012) Mass transport of nanocarriers. Pan Stanford, Boca Raton
Shah S (2009) Numerical simulation of particle adhesion dynamics for applications in nanomedicine and biosensing, University of Texas at Arlington
Shamloo A (2014) Cell-cell interactions mediate cytoskeleton organization and collective endothelial cell chemotaxis. Cytoskeleton 71(9):501–512
Shamloo A, Nejad MA, Saeedi M (2017). Fluid-structure interaction simulation of a cerebral aneurysm: effects of endovascular coiling treatment and aneurysm wall thickening. J Mech Behav Biomed Mater 74:72–83
Slack JD, Kanke M, Simmons GH, DeLuca PP (1981) Acute hemodynamic effects and blood pool kinetics of polystyrene microspheres following intravenous administration. J Pharm Sci 70(6):660–4
Sohrabi S, Zheng J, Finol EA, Liu Y (2014) Numerical simulation of particle transport and deposition in the pulmonary vasculature. J Biomech Eng 136(12):121010
Sohrabi S, Wang S, Tan J, Xu J, Yang J, Liu Y (2017) Nanoparticle transport and delivery in a heterogeneous pulmonary vasculature. J Biomech 50:240–247
Stadler AA, Zilow EP, Linderkamp O (1990) Blood viscosity and optimal hematocrit in narrow tubes. Biorheology 27(5):779–88
Tan J, Thomas A, Liu Y (2011) Influence of red blood cells on nanoparticle targeted delivery in microcirculation. Soft Matter 8:1934–1946
Tan J, Wang S, Yang J, Liu Y (2013) Coupled particulate and continuum model for nanoparticle targeted delivery. Comput Struct 122:128–134
Tangelder GJ, Teirlinck HC, Slaaf DW, Reneman RS (1985) Distribution of blood platelets flowing in arterioles. Am J Physiol 248(3):318–323
Thompson AJ, Mastria EM, Eniola-Adefeso O (2013) The margination propensity of ellipsoidal micro/nanoparticles to the endothelium in human blood flow. Biomaterials 34(23):5863–71
Tilles AW, Eckstein EC (1987) The near-wall excess of platelet-sized particles in blood flow: its dependence on hematocrit and wall shear rate. Microvasc Res 33(2):211–23
Tomey MI, Kini AS, Sharma SK (2014) Current status of rotational atherectomy. JACC Cardiovasc Interv 7(4):345–53
Traberg MS, Jensen JA (2014) Ultrasound evaluation of an abdominal aortic fluid-structure interaction model, pp 2292–2295
Umbarkar TS, Kleinstreuer C (2015) Computationally efficient fluid-particle dynamics simulations of arterial systems. Commun Comput Phys 17(02):401–423
van der Giessen AG, Groen HC, Doriot PA, de Feyter PJ, van der Steen AF, van de Vosse FN, Wentzel JJ, Gijsen FJ (2011) The influence of boundary conditions on wall shear stress distribution in patients specific coronary trees. J Biomech 44(6):1089–95
Verheugt FW, Gersh BJ, Armstrong PW (2006) Aborted myocardial infarction: a new target for reperfusion therapy. Eur Heart J 27(8):901–4
Wen J, Ding G, Jiang W, Wang Q, Zheng T (2014) Numerical simulation of compliant artery bypass grafts using fluid-structure interaction framework. ASAIO J 60(5):533–40
Woldhuis B, Tangelder GJ, Slaaf DW, Reneman RS (1992) Concentration profile of blood platelets differs in arterioles and venules. Am J Physiol 262(4 Pt 2):H1217–23
Xie X, Wang Y, Zhu H, Zhou H, Zhou J (2013) Impact of coronary tortuosity on coronary blood supply: a patient-specific study. PLoS One 8(5):e64564
Zhu SJ, Poon EK, Ooi AS, Moore S (2015) Enhanced targeted drug delivery through controlled release in a three-dimensional vascular tree. J Biomech Eng 137(3):031002
Acknowledgements
We would like to thank Doctor Amir Sajadieh the interventional cardiologist and attending physician of CT-Angio Department of Alzahra Hospital of Isfahan who provided insight and expertise that greatly assisted the research
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Forouzandehmehr, M., Shamloo, A. Margination and adhesion of micro- and nanoparticles in the coronary circulation: a step towards optimised drug carrier design. Biomech Model Mechanobiol 17, 205–221 (2018). https://doi.org/10.1007/s10237-017-0955-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10237-017-0955-x