Abstract
Tidally dominated coasts are directly affected not only by projected rise in mean sea level, but also by changes in tidal dynamics due to sea level rise and bathymetric changes. By use of a hydrodynamic model, which covers the entire German Bight (South-Eastern North Sea), we analyse the effects of sea level rise and potential bathymetric changes in the Wadden Sea on tidal current velocities. The model results indicate that tidal current velocities in the tidal inlets and channels of the Wadden Sea are increased in response to sea level rise. This is explained by the increased ratio of tidal prism to tidal inlet cross-sectional area, which is due to the characteristic hypsometry of tidal basins in the Wadden Sea including wide and shallow tidal flats and relatively narrow tidal channels. The results further indicate that sea level rise decreases ebb dominance and increases flood dominance in tidal channels. This is, amongst others, related to a decreased intertidal area again demonstrating the strong interaction between tidal wave and tidal basin hypsometry in the Wadden Sea. The bathymetry scenario defined in this study includes elevated tidal flats and deepened tidal channels, which is considered a potential future situation under accelerated sea level rise. Application of these bathymetric changes to the model mostly compensates the effects of sea level rise. Furthermore, changes in current velocity due to the altered bathymetry are in the same order of magnitude as changes due to mean sea level rise. This highlights the significance of considering potential bathymetric changes in the Wadden Sea for regional projections of the tidal response to sea level rise.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sea level rise affects tides on all spatial scales ranging from global scale, i.e. oceans (Pickering et al. 2017), to regional scale, i.e. continental shelves such as the European continental shelf (Pickering et al. 2012; Pelling et al. 2013; Pelling and Green 2014), and local scale, i.e. coastal waters such as the German Bight (Rasquin et al. 2020) and its estuaries (Seiffert et al. 2014). At the same time, tidal dynamics depend on the bathymetry. This is especially important in shelf seas like the North Sea and in extremely shallow coastal waters such as the Wadden Sea in the German Bight, where the tidal signal is strongly distorted and a large amount of tidal energy is dissipated (Stanev et al. 2014; Rasquin et al. 2020). Jacob et al. (2016) have shown that even relatively small bathymetric changes in the Wadden Sea (observed differences from 2000 to 2011) are able to substantially modify the local and remote response of tidal dynamics in the North Sea. Hence, for estimating future modifications of tidal dynamics in the German Bight, not only effects of sea level rise itself are relevant, but also feedbacks of bathymetric changes in the Wadden Sea that are induced by sea level rise. This is also important with regard to the estimation of coastal protection design heights (Arns et al. 2017). The model domains in existing process-based numerical modelling studies, which investigate the long-term morphodynamic response of the Wadden Sea to sea level rise (Dissanayake et al. 2012; Becherer et al. 2018), include only a single tidal basin. However, the hydro- and morphodynamic response of the Wadden Sea to accelerated sea level rise could be spatially diverse due to local differences in tidal forcing, sediment availability, and other factors. Therefore, the results of local models cannot be transferred to the Wadden Sea in general. In this study, we use a hydrodynamic model that covers almost the entire Wadden Sea with a resolution that allows to draw more general conclusions regarding the tidal response of the Wadden Sea to a rise in sea level and to evaluate regional differences within the Wadden Sea.
The aim of our study is threefold. Firstly, we investigate the tidal response to a sea level rise of 0.8 m, which represents a likely estimate for the end of the twenty-first century in case of the emission scenario RCP8.5 defined by the IPCC (Church et al. 2013). Secondly, based on an extensive literature research, we estimate potential, systematic morphologic changes in the Wadden Sea in response to an accelerated sea level rise within the twenty-first century. We transfer these findings into schematic changes of the model bathymetry (Section 2.3). Thirdly, we analyse the hydrodynamic feedbacks of the changes applied to the model bathymetry. We compare the effects of these bathymetric changes in the Wadden Sea to the effects of sea level rise. Special emphasis is placed on whether the changes induced by the bathymetric changes compensate or reinforce the changes induced by sea level rise. The results are mainly analysed in terms of maximum flood and maximum ebb current velocity as well as the ratio between both as these parameters are most suitable to demonstrate changes in tidal asymmetries in tidal inlet systems. In turn, the focus on tidal asymmetry of current velocity is largely motivated by its significance for the residual transport of sediment and thus the morphologic development of the Wadden Sea. The structure of this paper is as follows. A short description of the model setup, the model validation, the applied scenarios (sea level rise and bathymetric change), and applied analysis methods follows in Section 2. Results are elaborated in Section 3. Section 4 discusses the physical processes, which could be responsible for the observed effects of sea level rise and bathymetric changes, respectively. Finally, a conclusion is given in Section 5.
2 Methods
2.1 Hydrodynamic model and model setup
For this study, the three-dimensional hydrodynamic model UnTRIM is used that solves the shallow water equations on an unstructured grid, consisting of triangles and rectangles (Casulli and Walters 2000). This model is suitable for the simulation of complex, three-dimensional flows. An unstructured grid enables an efficient spatial resolution in environments of complex bathymetry as it can be fitted to morphologic structures and allows for a highly variable model resolution. Therefore, it is especially appropriate for the simulation of tidal flows in the Wadden Sea with its intertidal flats intersected by a morphologically diverse channel system including highly curved channels (Fig. 1). The model contains a flooding and drying scheme (Casulli and Walters 2000), which is important for the correct simulation of non-linear hydrodynamic effects in tidally dominated, shallow coastal waters like the Wadden Sea, where the mean depth is comparable with the tidal range.
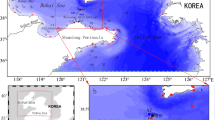
Domain of the German Bight model with locations of tide gauges (red dots) used for validation (water-level stations shown in Fig. 2 are marked with a yellow frame). The shallow areas with elevations between ± 1 mNHN roughly represent the intertidal flats of the Wadden Sea. The grey-dashed box denotes the area used for evaluation of model results. The domain of the shelf model is given on the right; within this map, the position of the German Bight model is indicated
The model covers the entire German Bight (Fig. 1) and comprises almost the entire Wadden Sea except for the Western part of the Dutch Wadden Sea. The three major estuaries of the German Bight (rivers Elbe, Weser, and Ems) are included up to the weirs defining the tidal limit. The horizontal model resolution is highest in the coastal waters of the German Bight, i.e. in the Wadden Sea, estuaries, and foreshore area (between 100 and 400 m), and decreases continuously towards the open sea boundary (about 5000 m). The model grid consists of around 100,000 grid cells horizontally. A z-layer model is used to resolve the vertical dimension. The vertical resolution is 1 m up to a depth of 28 m and continuously decreases in several steps from 2 to 10 m for greater depths.
At the open sea boundary, the German Bight model is forced by water levels from the Dutch Continental Shelf Model DCSMv6FM, which is a further development of the Dutch Continental Shelf Model DCSMv6 (Zijl et al. 2013; Zijl et al. 2015). Since this shelf model covers the entire North-Western European continental shelf (Fig. 1), it captures shallow water effects generated on the shelf. Sea level rise is introduced by adding a constant value to water levels at the open boundary of the shelf model. In this way, shallow water effects on the shelf and its potential changes with sea level rise are included in the forcing of the regional German Bight model. In turn, we assume that along the open boundary of the shelf model, which is located in the deep ocean of the North Atlantic, tidal forcing is not significantly changed in response to the considered sea level rise of 0.8 m according to findings of e.g. Pickering et al. (2017), who predict M2 amplitude changes between − 2 and + 2 cm along the open boundary of the shelf model for a sea level rise of 2 m.
In the German Bight model as well as in the shelf model, wind friction is induced by atmospheric forcing (wind fields and atmospheric pressure at 10 m above sea surface) from the reanalysis data COSMO-REA6 with a resolution of approximately 6 km (Hans-Ertel-Centre for Weather Research; Bollmeyer et al. 2015). While the effect of wind forcing on currents and surge is included in the model, the generation of wind waves is not included. The German Bight model includes transport of salt. Local bed friction is calculated according to spatially constant ripple roughness and spatially variable grain roughness, which is based on the measured sediment distribution (assembled by Milbradt et al. 2015b). River discharge at the landward open boundaries in the three estuaries of the rivers Elbe, Weser, and Ems is based on measurements from the Federal Waterways and Shipping Administration (WSV). The bathymetric data is mainly based on data provided by the DHI (Danish Hydrological Institute) and the BSH (Federal Maritime and Hydrographic Agency Germany). These data are updated with bathymetric data from the project AufMod (Milbradt et al. 2015b) in the shallow coastal zone.
2.2 Model validation
In the following, the validity of the German Bight model is analysed. Figure 2 shows time series of water levels from model simulations and measurements at four different stations within the German Bight (see Fig. 1 for positions) covering a full spring-neap tidal cycle in July 2010.
The tidal low water is generally overestimated, while the tidal high water is mostly underestimated by the model (Fig. 2). Thus, the tidal range is underestimated. Nevertheless, the model well captures the propagation of the tidal wave throughout the German Bight and its shallow coastal areas including general features like an increasing tidal range towards the inner German Bight (compare Fig. 2 b and c with Fig. 2 a and d) and an increasing distortion of the tidal signal towards the coast. The overall agreement of the simulation with measurements is also confirmed by rather small values for the root mean square error (RMSE) (0.22 m on average), root mean square difference (uRMSD) (0.21 m on average), and bias (0.08 m on average) as well as by a high correlation (0.993 on average) and a normalised standard deviation near 1 (0.83 on average) as shown in Fig. 3 and Table 1 (see Fig. 1 for positions of water-level stations). The standard deviation for simulation and measurement demonstrates the average magnitude of water-level deviations from the respective mean water level and thus roughly represents the half of the simulated or measured tidal range. The normalised standard deviation is the ratio of the standard deviation of the simulation relative to the standard deviation of the measurements. It is an indicator of how well the simulated tidal range fits to the measurements and if the tidal range is overestimated (in case of STD* > 1) or underestimated (in case of STD* < 1) by the model. Locations with largest deviations between model and observation are located at the North Frisian coast, while the locations at the East Frisian coast show smaller differences (Fig. 3). Within the estuaries, tidal dynamics are represented well with smallest errors obtained in the Weser and Elbe estuaries (Fig. 3). Overall, it is concluded that the model validity is sufficient to correctly determine regional-scale changes of tidal dynamics in response to changes in sea level or bathymetry.
Validation of simulated water levels against measurements at different stations in the German Bight (see Fig. 1 for positions) by means of the Taylor diagram including normalised standard deviation STD* (see Table 1 for the respective standard deviation of simulation and measurement), correlation, and the resultant normalised root mean square difference (uRMSD*). The correlation represents how the shape of the simulated and measured water-level curves fits to each other. The uRMSD demonstrates the relative frequency of outliers as larger errors have a disproportionately large effect on uRMSD. In turn, the uRMSD* compares the simulated frequency of outliers relative to measurements. A perfect fit is located at a correlation of 1 (on the x-axis), a STD* of 1, and a uRMSD* of 0
2.3 Setup of a bathymetry scenario for the Wadden Sea
The bathymetry scenario applied in this study is based on a literature review and aims at representing a first approximation of the morphodynamic response of the Wadden Sea to a sea level rise of 0.8 m within the twenty-first century.
A fundamental assumption of the bathymetry scenario considered in this study is the existence of a theoretical morphological equilibrium state of a tidal inlet system composed of the morphologic macro elements tidal inlet (and channels), tidal flats, and (sometimes) ebb tidal delta. When the hydrodynamic conditions change (e.g. due to mean sea level rise), the net sediment exchange between these morphologic macro elements is adjusted to attain a new state of morphological equilibrium. Therefore, the morphological development of the different elements should not be considered isolated from each other (De Vriend 1996, van Goor et al. 2003). The morphologic macro elements are likely to respond with different vertical adjustments in response to sea level rise, especially in case of a high rate of sea level rise, such as the scenario investigated in this study (0.8 m per century). Sea level rise induces an increase of residual sediment transport from the ebb tidal deltas and channels to the flats (van Goor et al. 2003; Hofstede 2002), which leads to accretion of tidal flats as well as to erosion of tidal inlets and potentially ebb tidal deltas. Therefore, the bathymetry scenario as defined herein includes different changes in height for tidal channel systems and tidal flats, respectively.
Based on the preceding considerations, qualitative estimates for the vertical adjustment of the morphologic macro elements in tidal basins of the Wadden Sea can be made including a vertical growth of tidal flats and a deepening of tidal inlets and channel systems. However, for the setup of a bathymetry scenario, specific values for these vertical adjustments need to be defined. Based on numerical modelling studies of e.g. Dissanayake et al. (2012) or Becherer et al. (2018), a valid assumption in the setup of the bathymetry scenario is that the tidal flat growth is not sufficient to fill the sediment deficit created by an accelerated sea level rise of 0.8 m within the twenty-first century. For this sea level rise scenario, we assume a vertical growth of tidal flats by 0.5 m, which lies in between the mean sea level rise of the last few thousand years (~ 0.1 to 0.2 m per century), that was fully balanced by tidal flat growth, and a tidal flat growth, which would fully balance the considered sea level rise of 0.8 m.
The potential of tidal flats to adapt morphodynamically to an accelerated sea level rise by accretion significantly depends on the sediment availability (van Goor et al. 2003). In turn, sediment availability depends on both internal and external sediment sources. External sediments are potentially provided by the foreshore area, barrier islands, ebb tidal deltas, or fluvial input and may originate from distant sites as sediments in the nearshore coastal waters of the German Bight are transported via alongshore transport pathways (Zeiler et al. 2000 and references therein; Zeiler et al. 2014; Milbradt et al. 2015a; Valerius et al. 2015). With regard to the results of Dissanayake et al. (2012) and Becherer et al. (2018), it is assumed that the sediment availability from external sediment sources will not be sufficient to completely balance the sediment demand that is created on the tidal flats in case of significantly accelerated sea level rise. In this case, an increasing amount of sediment from internal sediment sources (tidal inlet, channels, and possibly ebb tidal delta) is supposed to additionally fill the sediment demand on the tidal flats (de Ronde and de Ruijter 1987; Hofstede 2002) leading to erosion of the tidal inlet as reported by Dissanayake et al. (2012), Becherer et al. (2018), and van Maanen et al. (2013). Accordingly, for the scenario of 0.8 m of sea level rise within the twenty-first century, we assume a deepening of the tidal channel systems by 0.2 m in our bathymetry scenario, which implicates the assumption that roughly a third of the added tidal flat volume originates from the tidal channels. Our assumption that tidal flats and tidal channels may experience different trends in elevation changes is further supported by an aggregated analysis of morphodynamic observations indicating accretion on tidal flats and erosion in tidal channels in most tidal basins of the German Wadden Sea in the period from 1998 to 2016 (Benninghoff and Winter 2019). In our bathymetry scenario, the elevation and lateral extension of the ebb tidal deltas is not changed, since the individual morphodynamic response of ebb tidal deltas to sea level rise strongly depends on sediment supply and thus could be diverse. For example, while Dissanayake et al. (2012) observe an erosion of the ebb tidal delta, van Maanen et al. (2013) observe an expansion towards the open sea.
We point out that the bathymetry scenario defined here represents a first estimate of systematic changes in the Wadden Sea bathymetry under a sea level rise of 0.8 m towards the end of the twenty-first century and thus includes assumptions and simplifications, which we summarise in the following.
First, for the barrier islands of the East Frisian Wadden Sea, a landward shift has been proposed for a future rise in sea level (Flemming and Bartholomä 1997). However, barrier islands are excluded from the model domain, which implies the assumption of stable barrier islands in accordance with current coastal protection policies.
Second, wind waves are known to have a mainly erosional effect on tidal flats (Bartholomä et al. 2009; Hirschhäuser and Zanke 2004; Wilkens and Mayerle 2005; Lettmann et al. 2009). This erosional effect of wind waves may increase as sea level rise increases the water depth. However, we assume that (for the considered scenario of 0.8 m rise in sea level by the end of the twenty-first century) the export of sediment induced by wind waves will not exceed the total import of sediment induced by mechanisms including flood-dominant tidal current asymmetry related to overtide formation (Speer and Aubrey 1985; Friedrichs and Aubrey 1988), landward decrease in tidal current amplitude in combination with settling lag and scour lag effects (van Straaten and Kuenen 1957; Postma 1961; Groen 1967; Hoitink 2003; Pritchard and Hogg 2003; Gatto et al. 2017), and gravitational circulation induced by horizontal density gradients (i.e. mainly due to salinity gradients) in combination with tidal straining (Burchard et al. 2008; Burchard and Hetland 2010; Flöser et al. 2011; Burchard and Badewien 2015). Also note that the wind intensity is assumed to remain unchanged throughout the twenty-first century, since no significant long-term changes of wind speed over the North Sea could be detected in ensembles of recent model projections (Ganske et al. 2016). With regard to our bathymetry scenario, these considerations further support our assumption that tidal flats will be generally elevated and not deepened.
Finally, we do not consider the effects of conditions or mechanisms, which are potentially relevant for sediment dynamics and budgets on a rather local scale and which could result in regionally different morphologic developments within the Wadden Sea. These include:
-
(1)
Sediment availability (e.g. van Goor et al. 2003; Maan et al. 2018), which depends on the suspended sediment concentration at the seaward boundary of the tidal inlet system, i.e. in the nearshore zone of the German Bight (Puls et al. 1999; Gayer et al. 2006), the magnitude of the alongshore transport (“sediment bypassing”) off the Wadden Sea (Zeiler et al. 2000; Zeiler et al. 2014), the riverine input in the vicinity of estuaries (Gayer et al. 2006), the erodibility of tidal channels and foreshore area (Ricklefs and Asp Neto 2005), and anthropogenic sand supply (Stive et al. 2013)
-
(2)
Composition of available sediment, i.e. availability of fine sediments (silt and clay) affecting the growth rate of tidal flats (van Ledden et al. 2004) and the general stability of sand beds (e.g. Le Hir et al. 2011; Bartzke et al. 2013)
-
(3)
Tidal range affecting the ability to import the available sediment (e.g. van der Wegen 2013; Hofstede et al. 2016)
-
(4)
Tidal basin–specific geometry affecting tidal asymmetries (e.g. Dronkers 1986; Friedrichs et al. 1990) and related residual sediment transports
-
(5)
Exposure of tidal flats to wind (Allen and Duffy 1998; Fagherazzi and Wiberg 2009) and tidal inlet depth and orientation relative to the dominant wind direction affecting the propagation of swell into the tidal basin
-
(6)
Biological effects on the non-vegetated tidal flats (Kraeuter and Wetzel 1986; Hirschhäuser 2003; Beukema 2002) and on the salt marshes (Mariotti and Fagherazzi 2010; Kirwan and Megonigal 2013; Best et al. 2018)
-
(7)
Anthropogenic changes in bathymetry and tidal basin geometry, including the construction of hard structures such as dams along tidal watersheds (Ahrendt 2006), the reduction of tidal basin size as a result of land reclamation (Elias et al. 2012; Becherer et al. 2018), subsurface deepening as a result of gas extraction (Dijkema 1997; Marquenie and Vlas 2005; van Thienen-Visser et al. 2015), and the deepening of navigational channels (Benninghoff and Winter 2018).
Note that in contrast to these local factors, sea level rise is a global factor, which is relevant within the entire Wadden Sea.
2.4 Model simulations and analysis
To analyse the effects of sea level rise and bathymetric changes, we perform three simulations. The first simulation represents the reference condition, which does not include any changes in sea level or model bathymetry. The second simulation includes a sea level rise of 0.8 m, which is introduced at the ocean boundary of the shelf model (Section 2.1). The third simulation includes a sea level rise of 0.8 m and bathymetric changes in the Wadden Sea according to the scenario described in Section 2.3. The simulations cover a period in summer 2010 with generally low wind speed and low to moderate discharge from the Elbe, Weser, and Ems rivers.
The 2-week period used for tidal analysis (06–21 July 2010) starts after a model spin-up of around 5 weeks and covers a full spring-neap tidal cycle corresponding to 28 semi-diurnal tidal cycles (≈ 15 days). Tidal characteristics are calculated on the basis of a time series analysis on each grid cell edge and are temporally averaged or integrated over at least one tidal cycle. For further details on the techniques of the applied tidal analysis, the reader is referred to Lang (2003) or BAW (2017).
In this study, we focus on the analysis of tidal current velocity i.e. the changes in tidal current velocity in response to the simulated sea level rise as well as in response to the applied bathymetric changes. Note that the definition of ebb or flood dominance can be based on various characteristics of tidal current velocity (e.g. ratios of mean flood/ebb current velocity, maximum flood/ebb current velocity, flood/ebb current duration), which may reveal opposite directions (Fofonova et al. 2019). Here we mainly use the ratio of maximum flood current velocity to maximum ebb current velocity for identification of tidal asymmetry. Changes in tidal current velocities give first-order indications for potential morphodynamic changes in the tidal inlets of the Wadden Sea, where tidal currents have been suggested to be the main driver of morphologic activity by using a simplistic manner of data assimilation (annual topographies) in morphodynamic modelling (Kösters and Winter 2014). In turn, the focus on tidal asymmetry of current velocity is largely motivated by its significance for the residual transport of sediment and thus the morphologic development (sediment budget) of the tidal flats of the Wadden Sea.
3 Results
3.1 Reference condition
On the tidal flats, flood current velocity (Fig. 4a) is generally stronger than ebb current velocity (Fig. 4b) indicating flood dominance (red areas in Fig. 4c). In contrast, many tidal channel systems generally reveal no flood dominance at all or only weak flood dominance in a few subsections. In fact, the seaward reaches of the tidal inlets (in the vicinity of the ebb tidal deltas) rather show ebb dominance (blue areas in Fig. 4c). This spatial pattern is especially significant in the tidal inlets of the East Frisian Wadden Sea. Hence, tidal flats and tidal channels reveal significant differences in tidal asymmetry of current velocity. Finally, the tidal inlet systems of the German Wadden Sea reveal regional differences in tidal asymmetry as indicated by the ratio of maximum flood current velocity to maximum ebb current velocity (Fig. 4c) and the flood current duration (Fig. 4d). Note that the tidal current velcities and tidal asymmetries described here are vertically averaged and that deviations from the vertical average may exist along the water column, in particular in the deeper sections of the channel-systems, i.e. in the tidal inlets (Stanev et al. 2007).
3.2 Effects of sea level rise
In response to a sea level rise of 0.8 m, the model simulates a general increase in mean tidal current velocity (vmean) in the tidal inlets of the Wadden Sea (Fig. 5a). The response of vmean on the tidal flats is less systematic and reveals stronger regional differences. On the tidal flats behind barrier islands (East Frisian Wadden Sea), a general reduction of vmean is observed, whereas the tidal flats of the open-coast Wadden Sea (central German Bight), especially in the Elbe estuary, reveal a predominant increase of vmean (Fig. 5a).
Effect of the 0.8-m sea level rise on mean tidal current velocity vmean (a), maximum flood current velocity vf_max (b), maximum ebb current velocity ve_max (c), ratio of maximum flood current velocity to maximum ebb current velocity vf_max/ve_max (d), and flood current duration df (f). Ratio of maximum flood current velocity to maximum ebb current velocity vf_max/ve_max at the scenario of the 0.8-m sea level rise (e). The detailed view of a section of the East Frisian Wadden Sea in the insets of c and d is shown to better visualise the along-channel differences described in the text
The tidal inlets of the Wadden Sea reveal an increase in maximum flood current velocity (vf_max) typically with a maximum increase in the central section of tidal inlets, e.g. between barrier islands (Fig. 5b). Some channels also show an increase in maximum ebb current velocity (ve_max) (Fig. 5c). However, the increase in vf_max is generally larger than the increase in ve_max. Moreover, ve_max decreases in many parts of the tidal channel systems of the Wadden Sea (Fig. 5c), especially in the landward sections within the tidal basins as well as in some ebb tidal deltas (see the inset of a detailed view in Fig. 5c). As a result, the tidal channel systems of the Wadden Sea are generally characterised by an increased ratio of maximum flood current velocity to maximum ebb current velocity (vf_max/ve_max) (Fig. 5d). This implies a reinforcement of flood dominance, an attenuation of ebb dominance, or a reversion from ebb dominance to flood dominance (compare Fig. 4c and Fig. 5e). Prominent examples for an attenuation of ebb dominance are the ebb tidal deltas of the East Frisian Wadden Sea and the main channel of the outer Weser estuary. Many sections of tidal channel systems, which have no tidal asymmetry of current velocity in the reference case, show distinct flood dominance in response to sea level rise. These results are in agreement with findings of e.g. Stanev et al. (2006), French (2008), and Dissanayake et al. (2012). However, regional differences are obvious. While an increased vf_max/ve_max is observed within the entire tidal channel systems of the East Frisian Wadden Sea and central German Bight, the ratio is increased only in the landward reaches of the tidal channel systems of the North Frisian Wadden Sea. A maximum increase in vf_max/ve_max is often located in the landward sections of the channel systems (see the inset of a detailed view in Fig. 5d), which is primarily related to a decreased ve_max (see the inset of a detailed view in Fig. 5c). In response to sea level rise, the duration of the flood current (df) is shortened in the major tidal channels of the southern German Bight (Fig. 5f). This is consistent with the observed increase of vf_max/ve_max in these tidal channels (Fig. 5d).
On the tidal flats, vf_max and ve_max reveal a more complex and diverse response to sea level rise. While some tidal flats experience an increase in vf_max (e.g. in the outer Elbe estuary and Dithmarschen Wadden Sea), other tidal flats show a pronounced decrease in vf_max (e.g. in the eastern back barrier basins of the East Frisian Wadden Sea, the tidal basins near the island of Sylt, and the outer Ems estuary; Fig. 5b). Systematic spatial patterns are hardly observed, except for the back barrier basins in the East Frisian Wadden Sea, where a decrease in vf_max is concentrated along the tidal watersheds (Fig. 5b). The ve_max increases on many tidal flats of the Wadden Sea, in particular near tidal watersheds, on some tidal flats of the outer estuaries, and on the seaward tidal flat areas in the open-coast Wadden Sea of the central German Bight (Fig. 5c). Both vf_max and ve_max exclusively increase on the tidal flats of the outer Elbe estuary and the Dithmarschen Bight, which is in contrast to any other tidal basin of the Wadden Sea. The different tidal response to sea level rise on tidal flats compared with tidal channels observed in most of the Wadden Sea is in agreement with results of Stanev et al. (2006). Finally, vf_max/ve_max is increased or decreased on tidal flats and its changes reveal a spatially very heterogeneous pattern (Fig. 5d). Nevertheless, some systematic patterns can be observed. For example, a maximum decrease in vf_max/ve_max is often found on tidal watersheds or high tidal flats in general. The existing flood dominance on tidal flats (Fig. 4c) is reinforced or weakened, but usually not reversed into ebb dominance so that tidal asymmetry is still in favour of flood dominance on most tidal flats (Fig. 5e). Furthermore, the magnitude of changes of the ratio of maximum flood to maximum ebb current velocity on tidal flats differs between tidal basins. However, changes of these ratios are very sensitive in case of small flood or ebb current velocities, which is typically the case on tidal flats, and thus, they should not be assessed quantitatively on tidal flats.
3.3 Effects of bathymetric changes
This section describes the effects of the bathymetric changes applied to the model as described in Section 2.3 (tidal flats elevated by + 0.5 m and tidal channels deepened by − 0.2 m). To this end, we analyse the differences between the simulation with a sea level rise of 0.8 m and additional bathymetric changes and the simulation including solely sea level rise. The changes applied to the model bathymetry result in a decrease of maximum flood current velocity (vf_max) in tidal inlets and channels of the Wadden Sea (Fig. 6a). The maximum ebb current velocity (ve_max) in the seaward section of many tidal inlet systems also decreases (Fig. 6b), but to a lesser extent compared with vf_max. In the landward sections of some tidal channel systems, a slight increase in ve_max is observed, e.g. in the tidal basins between the Weser and Elbe estuaries. Although some tidal channels reveal no significant changes of vf_max/ve_max, this ratio decreases in many tidal channels in response to the bathymetric changes (Fig. 6c), mainly because of a strong decrease of vf_max. Hence, flood dominance is generally reduced in response to the bathymetric changes. Thus, with regard to tidal current velocities in tidal inlets and channels, the bathymetric changes compensate the systems response to mean sea level rise (Section 3.2). Nevertheless, the effects of bathymetric changes are not fully compensational as effects of sea level rise are usually stronger. The compensational effect of elevated intertidal areas compared with changes in tidal current velocity induced by sea level rise was also observed by French (2008) in a hydrodynamic model of the Blyth estuary (eastern England).
Effect of bathymetric changes on maximum flood current velocity vf_max (a), maximum ebb current velocity ve_max (b), and ratio of maximum flood current velocity to maximum ebb current velocity vf_max/ve_max (c). Ratio of maximum flood current velocity to maximum ebb current velocity vf_max/ve_max with the 0.8-m sea level rise and applied bathymetric changes (d)
On the tidal flats, vf_max and ve_max increase or decrease in response to the bathymetric changes, again with a sign which is predominantly contrary to the effect of sea level rise. For example, on some very high tidal flats, especially on tidal watersheds in the East Frisian Wadden Sea, the bathymetric changes induce an increase in vf_max (Fig. 6a), which is in contrast to the sea level rise effect (Fig. 5b). Most of the tidal flat areas, which exhibit an increase in ve_max due to sea level rise (Fig. 5c), show a decrease in ve_max in response to the bathymetric change (Fig. 6b), although the changes in ve_max are generally not as strong as the changes in vf_max. In general, the effect of the bathymetric changes on vf_max/ve_max compensates the effect of sea level rise (compare Fig. 6c with Fig. 5d). Consequently, not only in the tidal channels, but also on the tidal flats the effect of sea level rise on tidal current asymmetry is opposed by the effect of the applied bathymetric changes in most of the Wadden Sea.
The combined effect of sea level rise and bathymetric changes results in a spatial distribution of tidal asymmetries, which is comparable with the reference condition (compare Fig. 6d with Fig. 4c). The effects of both sea level rise and bathymetric changes on ve_max are not as strong as on vf_max. The effects of the bathymetric changes on tidal currents are generally smaller than the effects of sea level rise, but are in the same order of magnitude on the scale of a tidal basin. On a smaller scale (e.g. subsections of tidal channels or specific tidal flats), either sea level rise or bathymetric change can dominate the net response.
4 Discussion
4.1 Effects of sea level rise
The predicted effects of sea level rise on tidal currents can be summarised as follows. First, mean tidal current velocity is intensified in tidal inlets and channels. Second, flood dominance is strengthened and ebb dominance is weakened or transformed into flood dominance in the majority of the tidal inlet systems of the Wadden Sea. Third, changes in maximum flood and maximum ebb current velocity show along-channel differences in most of the tidal inlet systems. Fourth, in contrast to the tidal channels, the response of the tidal flats is less systematic, but mostly shows weakened flood dominance. Note that in this paper, we aim at understanding the mechanisms, which are responsible for the predicted response of tidal currents to sea level rise, rather than discussing the consequences for e.g. residual sediment transport which should be addressed in further studies.
4.1.1 Intensification of tidal currents in tidal inlets and channels
Friction is an important control of tidal dynamics on shelves and in shallow coastal waters. A rise in mean sea level increases the water depth and thereby reduces the frictional control promoting an increase of current velocity. However, a distinct relationship between increasing water depth and change in current velocity cannot be observed (note that the model predicts even a decrease of current velocity on some tidal flats although in general the relative change in water depth is largest there). This suggests that a reduced frictional control due to an increased water depth is not the only mechanism for the predicted changes in current velocity within the Wadden Sea and thus other physical controls need to be considered.
A rise in sea level increases the cross-sectional area of a tidal inlet (A′ > A, compare Fig. 7 a and b). As long as intertidal area is present in the initial condition, also the tidal prism must increase with sea level rise (P′ > P, compare Fig. 7 a and b), because in this case, the volume added to the tidal prism by the raised tidal high water is always larger than the volume removed from the tidal prism by the raised tidal low water, if we assume that tidal range does not decrease significantly. This even holds true for tidal basins, which are embanked along the line of the initial tidal high water and where no new shoal volume is added to the tidal prism. Due to the highly curved cross section of tidal inlet systems in the Wadden Sea, the relative increase of tidal prism (P′/P) is larger than the relative increase of cross-sectional area (A′/A) as illustrated in Fig. 7a, b. This explains the predicted general increase in mean tidal current velocity in the tidal inlets.
In case of a tidal inlet, which is narrower (and usually steeper) compared with its connected tidal basin (compare the two different cross-sectional profiles in Fig. 7c), a rise in sea level results in an even stronger increase of P/A (P′/A′ >> P/A, compare Fig. 7 c and d with Fig. 7 a and b), because with a narrower tidal inlet, A′/A is smaller than in case of a cross-sectional shape, which is constant in along-channel direction. This along-channel variation in cross-sectional width probably applies to all tidal inlet/basin systems of the Wadden Sea. An aggregation of the model results on individual tidal basins shows that P′/P is larger than A′/A in nearly all tidal inlet/basin systems of the Wadden Sea (Fig. 8).
Comparison of the relative change in cross-sectional flow area of tidal inlets (A′/A) with the relative change in tidal prism (flood volume) of the connected tidal basins (P′/P) induced by a sea level rise of 0.8 m with (P′/P)/(A′/A) = 1 represented by the dashed line (see Fig. 7 for definition of parameters). Each data point represents a tidal basin of the German Bight (the tidal basins used for analysis are displayed by red polygons)
We note that besides tidal basin hypsometry, the tidal prism is also determined by tidal range, which potentially changes with sea level rise. However, in the Wadden Sea, the relative change of tidal range induced by a sea level rise of 0.8 m (not shown here) is on average more than one order of magnitude smaller than the relative change of tidal prism. Thus, we conclude that in the Wadden Sea, the predicted change in tidal range is generally less important than the change in tidal basin hypsometry for the change in tidal prism and the related change in mean tidal current velocity. Nevertheless, since the change in tidal range induced by sea level rise is locally variable, its contribution to a change in tidal prism and related change in mean tidal current velocity is locally different ranging from negligible to moderate.
4.1.2 Changes of tidal asymmetries in tidal inlets and channels
Figure 9a shows the time series of transport rate in an exemplary tidal inlet (Otzumer Balje, see the black polygon in Fig. 8 for its position) for the reference case (green line) and the sea level rise scenario (blue line). In response to sea level rise, the transition from flood to ebb current around tidal high water occurs earlier, while the timing of the transition from ebb to flood around tidal low water is not changed. Hence, flood current duration is shortened in response to sea level rise, which has been observed already in the spatial analysis of the model results (Fig. 5f). This shortening of flood current duration in the tidal inlets of the Wadden Sea comes along with an increased ratio of maximum transport rate at flood to maximum transport rate at ebb (Fig. 9a), i.e. an enhanced flood dominance or weakened ebb dominance, as observed already in the spatial analysis of the ratio of (maximum) flood current velocity to (maximum) ebb current velocity (Fig. 5d). The time needed to establish maximum transport after slack water is generally much longer for flood than for ebb (Fig. 9a). This model result is in accordance with findings of Stanev et al. (2003a, 2003b) who demonstrate the dependency of this temporal asymmetry of transport on the hypsometry of tidal basins in the (East Frisian) Wadden Sea characterised by a large intertidal area (relative to total basin area) and a large storage capacity (or shoal volume). Here we show that this tidal asymmetry in the timing of maximum transport is weakened (however not reversed) by a sea level rise of 0.8 m as the maximum flood transport occurs earlier whereas the maximum ebb transport occurs later or is not temporally shifted (Fig. 9a). Stanev et al. (2003a) show that the excursion of transport including full physics is lagged compared with a case including only low-order dynamics and that the contribution of higher-order dynamical controls and thus its associated temporal lag effect on the transport rate is strongest between maximum flood and maximum ebb conditions. As the largest phase shifts of transport rate induced by sea level rise occur in this period (Fig. 9a), higher-order dynamical controls are suggested to contribute to the predicted tidal response to sea level rise. The non-linear response of tidal basins is controlled by the bottom slope in the intertidal areas (Stanev et al. 2003a; Hepkema et al. 2018). Accordingly the differential response of flood and ebb to sea level rise could be explained by the changed hypsometry (normalised by the basin area), i.e. the changed bottom slope of the landward shifted intertidal area. Due to the highly-curved hypsometry of tidal flats of the Wadden Sea, the bottom slope in the lower part of the intertidal area becomes flatter with a rise in sea level. At the same time the bottom slope in the upper part of the intertidal area becomes steeper with a rise in sea level, since most tidal basins of the Wadden Sea are embanked limiting the availability of new intertidal area (former supratidal area). Therefore, the intertidal area or storage capacity can be flooded much faster resulting in an earlier timing of maximum flood transport whereas the storage capacity added by new intertidal area is negligible in most tidal basins of the Wadden Sea resulting in an insignificant to moderate later timing of maximum ebb transport. This provides an explanation for the shortening of the flood associated with the asymmetric response of maximum transport rate at flood and ebb, respectively.
Time series of transport rate of the tidal inlet (a), relative change in cross-sectional flow area of the tidal inlet and volume of the tidal basin (b), and wet area of the tidal basin (c) for the Otzumer Balje (see the black polygon in Fig. 8 for its location). The reference case is represented by the green lines, the sea level rise scenario is represented by the blue lines, and the relative change in or difference between the respective parameters of the two scenarios is represented by the grey lines. In a, transport is defined positive towards the open ocean (ebb current)
As seen in Fig. 9b, the relative increase in water volume of the tidal basin (dashed line) is larger than the relative increase in cross-sectional flow area of the tidal inlet (solid line) throughout the entire tidal cycle both demonstrating an asymmetric response to sea level rise. While the relative increase in water volume of the tidal basin (dashed line in Fig. 9b) is largest around mid-flood, the relative increase in tidal inlet flow area (solid line in Fig. 9b) is largest around tidal low water. The resulting difference between both parameters is larger at flood than at ebb with the largest difference found at early to mid-flood (Fig. 9b). This is in accordance with the signal of transport rate (Fig. 9a) which reveals that the largest increase of flood transport occurs at early to mid-flood whereas the increase of ebb transport is distributed more equally throughout the ebb phase only with a small minimum at early ebb.
The geometric properties of the intertidal area (area relative to total basin area, bottom slope) represent an important hypsometric control on the tidal distortion in shallow tidal basins. A shift towards flood dominance in shallow tidal basins is often associated with a decrease of intertidal area or a decreased ratio of shoal volume to tidal channel volume (Boon and Byrne 1981; Speer and Aubrey 1985; Friedrichs and Aubrey 1988; Friedrichs and Madsen 1992), which is typically expected in embanked tidal basins in case of sea level rise (Dronkers 2005). This relation can also be seen in our exemplary tidal basin connected to the Otzumer Balje where the intertidal area (indicated by the tidal variation of wet area in Fig. 9c) decreases with sea level rise (compare the variations of the green and blue lines, respectively, in Fig. 9c). The decrease of intertidal area results from a smaller increase in the wet area around tidal high water compared with the increase in the wet area around tidal low water, which is likely related to the presence of dikes limiting the area available for flooding with sea level rise. Note that the tidal periods presented in Fig. 9 represent spring tide conditions. We are aware that the geometric properties of the tidal basins and the related hypsometric controls on tidal asymmetry may differ substantially under neap and spring tide conditions, respectively (Stanev et al. 2003b). However, since tidal asymmetry is not reversed between the two different conditions but simply more pronounced at spring tide, we assume that our conclusions from spring tide conditions are also valid for mean tide conditions in qualitative terms.
The discussed geometric and volumetric parameters may also largely explain the predicted regionally different responses of tidal asymmetry to sea level rise. For example, the weaker shift towards flood dominance in the tidal inlets of the North Frisian Wadden Sea compared with the tidal inlets of the East Frisian Wadden Sea could be related to the fact that the relative intertidal area of tidal basins in the North Frisian Wadden Sea (Spiegel 1997) is generally smaller than in the East Frisian Wadden Sea (Ferk 1995). Furthermore, the basin-specific widening from the inlet to the basin provides another explanation for regional differences in the response of tidal asymmetry to a rise in sea level. In this context, we note that the tidal inlets of the East Frisian Wadden Sea are usually narrower (more confined by barrier islands) than the tidal inlets of the North Frisian Wadden Sea. Also, Ridderinkhof et al. (2014) emphasise the importance of tidal inlet widening on the residual velocity in the inlet.
Note that tidal asymmetry is also generated by shallow water effects outside the Wadden Sea in the German Bight, i.e. in the open North Sea where hypsometric controls or tidal basin geometry in general is not relevant. In the German Bight, the tidal distortion is largely composed of the amplitude ratio of M2 and M4 and their relative phase difference (see e.g. Stanev et al. 2014 and Jacob et al. 2016 for a spatial analysis of numerical simulations). Hence, tidal inlet–specific changes in tidal asymmetry induced by sea level rise may also result from regionally different changes in the amplitude ratio of M2 and M4 and their relative phase difference which are already included in the forcing at the seaward boundary of the Wadden Sea.
The observed along-channel differences of the change in tidal asymmetry in response to sea level rise (Fig. 5d) could be related to the cross-section specific ratio of tidal flat width to tidal channel width which generally increases from the inlet towards the landward boundary of the tidal basins in the Wadden Sea (again representing a topographic control). Also, three-dimensional processes could be responsible for the observed along-channel differences including lateral circulation (Becherer et al. 2015; Pein et al. 2018) and vertical circulation (Stanev et al. 2007) which are both affected by the topography (geometric characteristics) of a tidal basin. Stanev et al. (2007) showed that the total transport at shallow channel sections is dominated by the surface layer transport which is controlled by a non-linear tidal response induced by the flooding and drying of tidal flats (inducing flood dominance). By contrast, the deeper channel sections (tidal inlets) are controlled by hypsometric properties of the tidal basin in the deeper layer (inducing ebb dominance) and by the tidally induced stokes drift in the upper layer (inducing flood dominance) compensating the seaward directed residual transport induced by the hypsometric control. Following Stanev et al. (2007), this vertical circulation provides an explanation for (vertically averaged) ebb dominance in tidal inlets and deep tidal channels and (vertically averaged) flood dominance in the shallow extensions of the channel system, which is confirmed by our model for the reference case (Fig. 4c). The vertical circulation is sensitive to relative changes in mean water depth of shallow tidal basins which in turn is different in along-channel direction in response to a rise in mean sea level (increasing towards the tidal flats). Hence, the predicted along-channel variation of the tidal response to sea level rise could also be related to depth-dependent variations of vertical circulation. In particular, the significant decrease in ebb current velocity in the shallower sections of the channel systems (Fig. 5c) could be the result of a diminishing hypsometric control formerly in part compensating the flood dominance induced by the non-linear response of tidal flats.
With regard to the tidal inlets and channels of the Wadden Sea, we conclude that the response of tidal asymmetry to sea level rise is strongly controlled by the tidal basin geometry, in particular by the presence of tidal flats (hypsometric control).
4.1.3 Changes of tidal current velocities on tidal flats
On many tidal flats of the Wadden Sea, the response of tidal dynamics to sea level rise is remarkably different than in tidal inlets and channels. The flood dominance prevailing on tidal flats in the reference condition (Fig. 4c) is weakened in many regions (Fig. 5d). However, it is also enhanced on some tidal flats (Fig. 5d). On intertidal flats, the extremely shallow water depth and the frequent flooding and drying result in a dominance of frictional effects. Therefore, we suggest that the flood dominance on the tidal flats being already present in the reference case is primarily related to the friction-induced generation of M4 (for theory, see Parker 1991; Friedrichs and Aubrey 1988; Guo et al. 2019) in combination with relative phase differences between M2 and M4 (2φM2–φM4 between 0 and 180°). The friction-induced formation of higher harmonics on tidal flats is very sensitive to changes in water depth. Therefore, with regard to the tidal flats, the response of tidal asymmetry to sea level rise is likely induced by changes in amplitudes of higher harmonics (mainly M4 and M6) and their interaction with the principal tidal component M2 by relative phase difference. In the German Wadden Sea, the M4 amplitude typically increases along the tidal channels towards the tidal flats (Stanev et al. 2014; Fofonova et al. 2019). Therefore, a change in 2φM2–φM4 induced by sea level rise will affect the tidal asymmetry particularly in the landward sections of tidal channel systems and on the tidal flats. Depending on the sign of the change in 2φM2–φM4, the flood dominance on tidal flats is either enhanced or weakened.
4.2 Further mechanisms
Baroclinic processes induced by the interaction of tidal currents with considerable fresh water input and related horizontal density gradients play a major role for generating residual circulation cells in estuaries (Geyer and MacCready 2014). Also, with regard to the Wadden Sea, the interaction of horizontal density gradients with tidal currents has been suggested to generate estuarine circulation and tidal mixing asymmetries which contribute to a net sediment import (Burchard et al. 2008; Flöser et al. 2011). However, compared with the Elbe, Weser, and Ems estuaries, fresh water input is usually about 2 orders of magnitude smaller in the semi-enclosed tidal basins of the German Wadden Sea (Gräwe et al. 2016). This results in an along-channel salinity gradient of tidal inlets which is about 1 order of magnitude smaller than in estuaries, e.g. 1–4 PSU in tidal inlets of the East Frisian Wadden Sea (Staneva et al. 2009) compared with ~ 30 PSU in the Elbe estuary with local gradients of up to 1 PSU/km (Stanev et al. 2015). Furthermore, temporal variability of local salinity in the tidal inlets of the Wadden Sea is much smaller compared with that in estuaries of the German Bight, e.g. up to 2 PSU on a tidal timescale in the East Frisian Wadden Sea (Staneva et al. 2009; Gräwe et al. 2016) compared with roughly 10 PSU on a tidal timescale in the seaward section of the Elbe estuaries (Stanev et al. 2019). Both the rather small horizontal density gradients and the small temporal variability of salinity are likely the main reasons for the relatively weak density–driven circulation in the German Wadden Sea as observed by Gräwe et al. (2016). Instead, Stanev et al. (2007) suggest that the tidal inlets of the (East Frisian) Wadden Sea are characterised by a vertical overturning cell that consists of a residual landward transport in the near-surface layer (dominated by the tidally induced Stokes drift) and a residual seaward transport in the deeper layer (dominated by the hypsometric control of the tidal basin), which is in contrast to classical estuarine circulation. Thus, with regard to the tidal inlets of semi-enclosed tidal basins of the German Wadden Sea, changes in baroclinic processes induced by sea level rise are expected to be less important compared with changes in barotropic processes discussed in Sections 4.1.1 and 4.1.2.
In the Wadden Sea, wind is an important mechanism for residual water exchange between tidal basins via the tidal watersheds (Herrling and Winter 2015; Sassi et al. 2015; Gräwe et al. 2016) as well as between tidal basins and the open North Sea via the tidal inlets (Herrling and Winter 2015; Lettmann et al. 2009). A rise in sea level potentially increases the importance of wind forcing for residual transport of water across tidal watersheds, since an increased water mass is stored on the tidal flats at slack water around high tide. However, with regard to tidal inlets, we assume that the effect of sea level rise on interactions between tidal currents and wind forcing is much smaller than its effect on interactions between tidal currents and tidal basin hypsometry or other characteristics of tidal basin geometry.
4.3 Effects of bathymetric changes in the Wadden Sea
In most parts of the Wadden Sea, the effect of the bathymetric changes applied to the model (elevation of tidal flats by 0.5 m, deepening of tidal channels by 0.2 m) compensates the effect of sea level rise on (maximum) flood current velocity, (maximum) ebb current velocity, and the tidal asymmetry between both. This holds true for both tidal channels and tidal flats. This result suggests that the predicted effects of the bathymetric changes are mainly a reversion of the mechanisms discussed in Section 4.1. The compensational effect of the bathymetric changes further supports the hypothesis that the tidal response to sea level rise in the Wadden Sea is primarily related to hypsometric control, since the applied bathymetric changes are essentially a systematic change in tidal basin hypsometry.
First of all, we note that the model predicts a decrease of current velocity in the tidal inlets of the Wadden Sea although the tidal inlets itself are deepened. This further demonstrates that reduced frictional control due to an increase in water depth cannot be the dominant control for the predicted changes of tidal current velocity in the Wadden Sea.
The applied elevation of tidal flats in the Wadden Sea reduces the shoal volume and thereby also the tidal prism of the tidal basins (P). This results in a general decrease of tidal current velocity in the tidal inlets. At the same time, the applied deepening of tidal channel systems increases the cross-sectional flow area in the tidal inlet (A). This further decreases the tidal current velocity in the tidal inlets. These considerations suggest that the observed decrease in mean tidal current velocity in the tidal inlets and channels (Fig. 5a) results from the decreased ratio of tidal prism to tidal inlet cross-sectional area (P/A).
The decrease in shoal volume is much larger than the increase in tidal channel volume, since the tidal flats are elevated by 0.5 m, while the tidal channels are deepened by only 0.2 m. This differential change is even larger, since the elevated tidal flat area is larger than the deepened tidal channel area in most tidal basins. This suggests that the changes of tidal asymmetry in the tidal channels are more effected by the elevated tidal flats than by the deepened tidal channels. This was also supported by simulations with an elevation of tidal flats by 0.5 m but without deepening of tidal channels (not shown here) which showed only minor differences of tidal current velocities and tidal asymmetry compared with the bathymetry scenario presented in this study.
While sea level rise decreases the maximum ebb current velocity in the most landward sections of tidal channel systems, maximum ebb current velocity increases again in these channel sections in response to the bathymetric changes. This compensational effect could be explained by along-channel differences in the channel-flat cross section, lateral or secondary circulation, and vertical circulation as discussed already in Section 4.1.2.
Also, on the tidal flats, the effects of the bathymetric changes are predominantly compensational, though mainly with regard to flood current velocity. Due to the elevated tidal flats, frictional effects and the friction-controlled generation of higher harmonics on tidal flats are expected to be reinforced. However, while the compensational effect of the bathymetric changes is pronounced in tidal channels, it is generally less intense and less systematic on the tidal flats suggesting that the locally dominant controls on the tidal response to sea level rise are more diverse on tidal flats compared with tidal channels. Thus, explanations for the tidal response on tidal flats are more difficult and need to be studied in more detail in future studies.
The predicted compensational effect of the bathymetric changes applied to our model indicates that the morphology of the tidal basins is closer to morphologic equilibrium (see Section 2.3) in comparison with the sea level rise simulation without bathymetric changes. This supports the plausibility of our bathymetry scenario for a sea level rise of 0.8 m assuming that sediment availability is sufficient to fill the tidal flat volume created in our bathymetry scenario.
Finally, the effects of the considered bathymetric changes have the same order of magnitude as the effects of the considered sea level rise. This highlights the importance of considering potential bathymetric changes in the highly dynamic Wadden Sea for local and regional projections of the tidal response to future sea level rise. The need to consider future changes of coastal morphology in addition to sea level rise was also recommended for a more comprehensive assessment of future coastal flooding by storm surges (Bilskie et al. 2014) and for coastal management in general (Passeri et al. 2015).
5 Conclusions
A hydrodynamic model of the German Bight is used to analyse the effects of a sea level rise of 0.8 m on tidal current velocity in the Wadden Sea. The model covers the entire German Wadden Sea and thus includes many different examples for tidal basin geometries and various conditions of tidal forcing. Furthermore, we set up a scenario of schematic bathymetric changes considered a likely morphodynamic response of the Wadden Sea to 0.8-m sea level rise within the twenty-first century and analyse its feedback effects on tidal current velocity. The setup of a bathymetry scenario is a compromise between the need for better knowledge of the hydrodynamic feedback of morphologic changes induced by projected sea level rise and the limitations of up-to-date process-based models for long-term morphodynamic predictions in a large and highly complex system like the Wadden Sea.
From the results of this study, we draw the following conclusions:
-
(1)
Sea level rise increases mean tidal current velocity in the tidal inlets of the Wadden Sea. This is explained by the increased ratio of tidal prism to tidal inlet cross-sectional area. With a rise in sea level, the tidal prism increases much more than the tidal inlet cross-sectional area, because of the characteristic morphology of tidal basins in the Wadden Sea including wide and shallow tidal flats and relatively narrow tidal channels generating a highly curved hypsometry.
-
(2)
The tidal inlets of the Wadden Sea become more flood dominant or less ebb dominant in response to sea level rise, which is associated with a shortened flood duration and a prolonged ebb duration. This change in tidal asymmetry is explained by hypsometric control which is reflected in a decreased intertidal area (or decreased ratio of tidal flat to channel area) favouring flood dominance.
-
(3)
In contrast to sea level rise, the elevation of tidal flats and deepening of tidal inlets and channels in the bathymetry scenario results in weakened flood dominance (or enhanced ebb dominance) in tidal inlets and channels mainly due to a decrease in flood current velocity (the change in ebb current velocity is rather weak). Thus, the systematic bathymetric changes in the Wadden Sea predominantly compensate the effect of sea level rise, which is again related to the strong hypsometric control on tidal asymmetry in short and shallow tidal basins.
-
(4)
Compared with the tidal inlets, the tidal flats show a spatially more heterogeneous tidal response to the rise in sea level as well as to the bathymetric changes though effects of sea level rise are again mainly compensated by the applied bathymetric changes. In contrast to tidal inlets and channels, the tidal response to sea level rise on tidal flats cannot be explained by hypsometric controls. Here, frictional effects and related changes in the relative phase difference between principal tidal components (mainly M2) and higher harmonics (mainly M4 and M6) as well as changes in the amplitude of higher harmonics (mainly M4 and M6) are suggested to be important.
-
(5)
Overall, the effects of the considered bathymetry scenario on tidal current velocity are in the same order of magnitude as the effects of the associated sea level rise scenario. This highlights the significance of considering potential bathymetric changes in the Wadden Sea for local and regional projections of the tidal response to sea level rise.
Our results confirm the theories of hypsometric control on tidal dynamics known from simple analytical models. However, as bathymetries of real tidal basins are highly individual, the use of a complex, process-based, and more realistic numerical model gives a better insight into the actual variety of the tidal response to sea level rise in real systems and has a particular high value for local coastal and estuarine management.
References
Ahrendt K (2006) Ein Beitrag zur holozänen Entwicklung Nordfrieslands. Die Küste 71:1–32
Allen JRL, Duffy MJ (1998) Medium-term sedimentation on high intertidal mudflats and salt marshes in the Severn Estuary, SW Britain: the role of wind and tide. Mar Geol 150:1–27
Arns A, Dangendorf S, Jensen J, Talke S, Bender J, Pattiaratchi C (2017) Sea-level rise induced amplification of coastal protection design heights. Sci Rep 7:40171. https://doi.org/10.1038/srep40171
Bartholomä A, Kubicki A, Badewien TH, Flemming BW (2009) Suspended sediment transport in the German Wadden Sea—seasonal variations and extreme events. Ocean Dyn 59:213–225. https://doi.org/10.1007/s10236-009-0193-6
Bartzke G, Bryan KR, Pilditch CA, Huhn K (2013) On the stabilizing influence of silt on sand beds. J Sediment Res 83:691–703. https://doi.org/10.2110/jsr.2013.57
BAW (2017) Analysis of calculated results. http://wiki.baw.de/en/index.php/Analysis_of_Calculated_Results. Accessed 16 April 2019
Becherer J, Stacey MT, Umlauf L, Burchard H (2015) Lateral circulation generates flood tide stratification and estuarine exchange flow in a curved tidal inlet. J Phys Oceanogr 45:638–656. https://doi.org/10.1175/JPO-D-14-0001.1
Becherer J, Hofstede J, Gräwe U, Purkiani K, Schulz E, Burchard H (2018) The Wadden Sea in transition - consequences of sea level rise. Ocean Dyn 68:131–151. https://doi.org/10.1007/s10236-017-1117-5
Benninghoff M, Winter C (2018) Decadal evolution of tidal flats and channels in the Outer Weser estuary, Germany. Ocean Dyn 68:1181–1190. https://doi.org/10.1007/s10236-018-1184-2
Benninghoff M, Winter C (2019) Recent morphologic evolution of the German Wadden Sea. Sci Rep 9:9293. https://doi.org/10.1038/s41598-019-45683-1
Best ÜSN, van der Wegen M, Dijkstra J, Willemsen PWJM, Borsje BW, Roelvink DJA (2018) Do salt marshes survive sea level rise?: modelling wave action, morphodynamics and vegetation dynamics. Environ Model Softw 109:152–166. https://doi.org/10.1016/j.envsoft.2018.08.004
Beukema JJ (2002) Expected changes in the benthic fauna of Wadden Sea tidal flats as a result of sea-level rise or bottom subsidence. J Sea Res 47:25–39. https://doi.org/10.1016/S1385-1101(01)00095-8
Bilskie MV, Hagen SC, Medeiros SC, Passeri DL (2014) Dynamics of sea level rise and coastal flooding on a changing landscape. Geophys Res Lett 41:927–934. https://doi.org/10.1002/2013GL058759
Bollmeyer C, Keller JD, Ohlwein C, Wahl S, Crewell S, Friederichs P, Hense A, Keune J, Kneifel S, Pscheidt I, Redl S, Steinke S (2015) Towards a high-resolution regional reanalysis for the European CORDEX domain. Q J R Meteorol Soc 141:1–15. https://doi.org/10.1002/qj.2486
Boon J, Byrne R (1981) On basin hypsometry and the morphodynamic response of coastal inlet systems. Mar Geol 40:27–48
Burchard H, Badewien TH (2015) Thermohaline residual circulation of the Wadden Sea. Ocean Dyn 65:1717–1730. https://doi.org/10.1007/s10236-015-0895-x
Burchard H, Hetland RD (2010) Quantifying the contributions of tidal straining and gravitational circulation to residual circulation in periodically stratified tidal estuaries. J Phys Oceanogr 40:1243–1262. https://doi.org/10.1175/2010JPO4270.1
Burchard H, Flöser G, Staneva JV, Badewien TH, Riethmüller R (2008) Impact of density gradients on net sediment transport into the Wadden Sea. J Phys Oceanogr 38:566–587. https://doi.org/10.1175/2007JPO3796.1
Casulli V, Walters RA (2000) An unstructured grid, three-dimensional model based on the shallow water equations. Int J Numer Meth Fluids 32:331–348
Church JA, Clark PU, Cazenave A, Gregory JM, Jevrejeva S, Levermann A, Merrifield MA, Milne GA, Nerem RS, Nunn PD, Payne AJ, Pfeffer WT, Stammer D, Unnikrishnan AS (2013) Sea level change. In: Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge and New York, pp 1137–1216
de Ronde JG, de Ruijter WP (1987) Die Auswirkungen eines verstärkten Meeresspiegelanstiegs auf die Niederlande. Die Küste:123–163
Dijkema KS (1997) Impact prognosis for salt marshes from subsidence by gas extraction in the Wadden Sea. J Coast Res 13:1294–1304
Dissanayake DMPK, Ranasinghe R, Roelvink JA (2012) The morphological response of large tidal inlet/basin systems to relative sea level rise. Clim Chang 113:253–276. https://doi.org/10.1007/s10584-012-0402-z
Dronkers J (1986) Tidal asymmetry and estuarine morphology. Neth J Sea Res 20:117–131
Dronkers J (2005) Dynamics of coastal systems. In: Advanced series in ocean engineering, vol 25. World Scientific, Singapore
Elias EPL, van der Spek AJF, Wang ZB, de Ronde J (2012) Morphodynamic development and sediment budget of the Dutch Wadden Sea over the last century. Neth J Geosci 91:293–310
Fagherazzi S, Wiberg PL (2009) Importance of wind conditions, fetch, and water levels on wave-generated shear stresses in shallow intertidal basins. J Geophys Res 114:211. https://doi.org/10.1029/2008JF001139
Ferk U (1995) Folgen eines beschleunigten Meeresspiegelanstiegs für die Wattgebiete der niedersächsischen Nordseeküste. Die Küste 57:135–156
Flemming BW, Bartholomä A (1997) Response of the Wadden Sea to a rising sea level: a predictive empirical model. Deutsche Hydrographische Zeitschrift 49:343–353. https://doi.org/10.1007/BF02764043
Flöser G, Burchard H, Riethmüller R (2011) Observational evidence for estuarine circulation in the German Wadden Sea. Cont Shelf Res 31:1633–1639. https://doi.org/10.1016/j.csr.2011.03.014
Fofonova V, Androsov A, Sander L, Kuznetsov I, Amorim F, Hass HC, Wiltshire KH (2019) Non-linear aspects of the tidal dynamics in the Sylt-Rømø Bight, south-eastern North Sea. Ocean Sci Discuss:1–38. https://doi.org/10.5194/os-2019-73
French JR (2008) Hydrodynamic modelling of estuarine flood defence realignment as an adaptive management response to sea-level rise. J Coast Res 2:1–12. https://doi.org/10.2112/05-0534.1
Friedrichs CT, Aubrey DG (1988) Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuar Coast Shelf Sci 27:521–545
Friedrichs CT, Madsen OS (1992) Nonlinear diffusion of the tidal signal in frictionally dominated embayments. J Geophys Res 97:5637–5650
Friedrichs CT, Aubrey DG, Speer PE (1990) Impacts of relative sea-level rise on evolution of shallow estuaries. Coast Estuar Stud 38:105–122
Ganske A, Tinz B, Rosenhagen G, Heinrich H (2016) Interannual and multidecadal changes of wind speed and directions over the North Sea from climate model results. Meteorol Z 25:463–478
Gatto VM, van Prooijen BC, Wang ZB (2017) Net sediment transport in tidal basins: quantifying the tidal barotropic mechanisms in a unified framework. Ocean Dyn 67:1385–1406. https://doi.org/10.1007/s10236-017-1099-3
Gayer G, Dick S, Pleskachevsky A, Rosenthal W (2006) Numerical modeling of suspended matter transport in the North Sea. Ocean Dyn 56:62–77. https://doi.org/10.1007/s10236-006-0070-5
Geyer WR, MacCready P (2014) The estuarine circulation. Annu Rev Fluid Mech 46:175–197. https://doi.org/10.1146/annurev-fluid-010313-141302
Gräwe U, Flöser G, Gerkema T, Duran-Matute M, Badewien TH, Schulz E, Burchard H (2016) A numerical model for the entire Wadden Sea: skill assessment and analysis of hydrodynamics. J. Geophys. Res. Oceans 121:5231–5251. https://doi.org/10.1002/2016JC011655
Groen P (1967) On the residual transport of suspended matter by an alternating tidal current. Neth J Sea Res 3:564–574
Guo L, Wang ZB, Townend I, He Q (2019) Quantification of tidal asymmetry and its nonstationary variations. J. Geophys. Res. Oceans 124:773–787. https://doi.org/10.1029/2018JC014372
Hepkema TM, de Swart HE, Zagaris A, Duran-Matute M (2018) Sensitivity of tidal characteristics in double inlet systems to momentum dissipation on tidal flats: a perturbation analysis. Ocean Dyn 68:439–455. https://doi.org/10.1007/s10236-018-1142-z
Herrling G, Winter C (2015) Tidally- and wind-driven residual circulation at the multiple-inlet system East Frisian Wadden Sea. Cont Shelf Res 106:45–59. https://doi.org/10.1016/j.csr.2015.06.001
Hirschhäuser T (2003) Morphodynamische Modellierung der Biodeposition in einem Testfeld der Dithmarscher Bucht. Die Küste 67:23–50
Hirschhäuser T, Zanke U (2004) Langfristige Sedimentdynamik des Systems Tidebecken-Ebbdelta unter besonderer Berücksichtigung von verändertem Seegang und Wasserständen. Die Küste 68:201–248
Hofstede J (2002) Morphologic responses of Wadden Sea tidal basins to a rise in tidal water levels and tidal range. Z Geomorph N F 46:93–108
Hofstede JLA, Becherer J, Burchard H (2016) Are Wadden Sea tidal systems with a higher tidal range more resilient against sea level rise? J Coast Conserv 22:71–78. https://doi.org/10.1007/s11852-016-0469-1
Hoitink AJF (2003) Flow asymmetry associated with astronomical tides: implications for the residual transport of sediment. J Geophys Res 108:185. https://doi.org/10.1029/2002JC001539
Jacob B, Stanev EV, Zhang YJ (2016) Local and remote response of the North Sea dynamics to morphodynamic changes in the Wadden Sea. Ocean Dyn 66:671–690. https://doi.org/10.1007/s10236-016-0949-8
Kirwan ML, Megonigal JP (2013) Tidal wetland stability in the face of human impacts and sea-level rise. Nature 504:53–60. https://doi.org/10.1038/nature12856
Kösters F, Winter C (2014) Exploring German Bight coastal morphodynamics based on modelled bed shear stress. Geo-Mar Lett 34:21–36. https://doi.org/10.1007/s00367-013-0346-y
Kraeuter JN, Wetzel RL (1986) Surface sediment stabilization-destabilization and suspended sediment cycles on an intertidal mudflat. In: Wolfe DA (ed) Estuarine variability. Academic Press, pp 203–223
Lang G (2003) Analyse von HN-Modell-Ergebnissen im Tidegebiet. Mitteilungsblatt der Bundesanstalt für Wasserbau 86:101–108
Le Hir P, Cayocca F, Waeles B (2011) Dynamics of sand and mud mixtures: a multiprocess-based modelling strategy. Cont Shelf Res 31:135–149. https://doi.org/10.1016/j.csr.2010.12.009
Lettmann KA, Wolff J-O, Badewien TH (2009) Modeling the impact of wind and waves on suspended particulate matter fluxes in the East Frisian Wadden Sea (southern North Sea). Ocean Dyn 59:239–262. https://doi.org/10.1007/s10236-009-0194-5
Maan DC, van Prooijen BC, Wang ZB (2018) Progradation speed of tide-dominated tidal flats decreases stronger than linearly with decreasing sediment availability and linearly with sea level rise. Geophys Res Lett 46:262–271. https://doi.org/10.1029/2018GL079933
Mariotti G, Fagherazzi S (2010) A numerical model for the coupled long-term evolution of salt marshes and tidal flats. J Geophys Res 115:77. https://doi.org/10.1029/2009JF001326
Marquenie JM, Vlas J (2005) The impact of subsidence and sea level rise in the Wadden Sea: prediction and field verification. In: Vermaat J, Salomons W, Bouwer L, Turner K (eds) Managing European coasts. Springer, Berlin, Heidelberg
Milbradt P, Kösters F, Putzar B, Plüß A (2015a) Analyse des Sedimenttransports und der Morphodynamik in der Deutschen Bucht auf Basis des Multi-Modell-Ansatzes. Die Küste 83:147–165
Milbradt P, Valerius J, Zeiler M (2015b) Das Funktionale Bodenmodell: Aufbereitung einer konsistenten Datenbasis für die Morphologie und Sedimentologie. Die Küste 83:19–38
Parker BB (1991) The relative importance of the various nonlinear mechanisms in a wide range of tidal interactions (review). In: Parker BB (ed) Tidal hydrodynamics
Passeri DL, Hagen SC, Medeiros SC, Bilskie MV, Alizad K, Wang D (2015) The dynamic effects of sea level rise on low-gradient coastal landscapes: a review. Earth’s Future 3:159–181. https://doi.org/10.1002/2015EF000298
Pein J, Valle-Levinson A, Stanev EV (2018) Secondary circulation asymmetry in a meandering, partially stratified estuary. J Geophys Res Oceans 123:1670–1683. https://doi.org/10.1002/2016JC012623
Pelling HE, Green JAM (2014) Impact of flood defences and sea-level rise on the European Shelf tidal regime. Cont Shelf Res 85:96–105. https://doi.org/10.1016/j.csr.2014.04.011
Pelling HE, Green JAM, Ward SL (2013) Modelling tides and sea-level rise: to flood or not to flood. Ocean Model 63:21–29. https://doi.org/10.1016/j.ocemod.2012.12.004
Pickering MD, Wells NC, Horsburgh KJ, Green JAM (2012) The impact of future sea-level rise on the European Shelf tides. Cont Shelf Res 35:1–15. https://doi.org/10.1016/j.csr.2011.11.011
Pickering MD, Horsburgh KJ, Blundell JR, Hirschi JJ-M, Nicholls RJ, Verlaan M, Wells NC (2017) The impact of future sea-level rise on the global tides. Cont Shelf Res 142:50–68. https://doi.org/10.1016/j.csr.2017.02.004
Postma H (1961) Transport and accumulation of suspended matter in the Dutch Wadden Sea. Neth J Sea Res 1:148–190
Pritchard D, Hogg AJ (2003) Cross-shore sediment transport and the equilibrium morphology of mudflats under tidal currents. J. Geophys. Res 108(11):1–15. https://doi.org/10.1029/2002JC001570
Puls W, van Beusekom J, Brockmann U, Doerffer R, Hentschke U, König P, Murphy D, Mayer B, Müller A, Pohlmann T (1999) SPM concentrations in the German Bight: comparison between a model simulation and measurements. Deutsche Hydrographische Zeitschrift 51:221–244
Rasquin C, Seiffert R, Wachler B, Winkel N (2020) The significance of coastal bathymetry representation for modelling the tidal response to mean sea level rise in the German Bight. Ocean Sci 16:31–44. https://doi.org/10.5194/os-16-31-2020
Ricklefs K, Asp Neto NE (2005) Geology and morphodynamics of a tidal flat area along the German North Sea coast. Die Küste:93–127
Ridderinkhof W, Swart HE, van der Vegt M, Alebregtse NC, Hoekstra P (2014) Geometry of tidal inlet systems: a key factor for the net sediment transport in tidal inlets. J Geophys Res Oceans 119:6988–7006. https://doi.org/10.1002/2014JC010226
Sassi M, Duran-Matute M, van Kessel T, Gerkema T (2015) Variability of residual fluxes of suspended sediment in a multiple tidal-inlet system: the Dutch Wadden Sea. Ocean Dyn 65:1321–1333. https://doi.org/10.1007/s10236-015-0866-2
Seiffert R, Hesser F, Büscher A, Fricke B, Holzwarth I, Rudolph E, Sehili A, Seiß G, Winkel N (eds) (2014) Auswirkungen des Klimawandels auf die deutsche Küste und die Ästuare: Mögliche Betroffenheiten der Seeschifffahrtsstraßen und Anpassungsoptionen hinsichtlich der veränderten Hydrodynamik und des Salz- und Schwebstofftransports. Schlussbericht KLIWAS-Projekt 2.04/3.02. KLIWAS Schriftenreihe. KLIWAS-36/2014
Speer PE, Aubrey DG (1985) A study of non-linear tidal propagation in shallow inlet/estuarine systems: part II: theory. Estuar Coast Shelf Sci 21:207–224
Spiegel F (1997) Morphologische Charakterisierung der Tidebecken des schleswig-holsteinischen Wattenmeeres vor dem Hintergrund säkularer Meeresspiegeländerungen. Die Küste 59:115–142
Stanev EV, Flser G, Wolff J-O (2003a) First- and higher-order dynamical controls on water exchanges between tidal basins and the open ocean. A case study for the East Frisian Wadden Sea. Ocean Dyn 53:146–165. https://doi.org/10.1007/s10236-003-0029-8
Stanev EV, Wolff J-O, Burchard H, Bolding K, Flöser G (2003b) On the circulation in the East Frisian Wadden Sea: numerical modeling and data analysis. Ocean Dyn 53:27–51. https://doi.org/10.1007/s10236-002-0022-7
Stanev EV, Wolff J-O, Brink-Spalink G (2006) On the sensitivity of the sedimentary system in the East Frisian Wadden Sea to sea-level rise and wave-induced bed shear stress. Ocean Dyn 56:266–283. https://doi.org/10.1007/s10236-006-0061-6
Stanev EV, Flemming BW, Bartholomä A, Staneva JV, Wolff J-O (2007) Vertical circulation in shallow tidal inlets and back-barrier basins. Cont Shelf Res 27:798–831. https://doi.org/10.1016/j.csr.2006.11.019
Stanev EV, Al-Nadhairi R, Staneva J, Schulz-Stellenfleth J, Valle-Levinson A (2014) Tidal wave transformations in the German Bight. Ocean Dyn 64:951–968. https://doi.org/10.1007/s10236-014-0733-6
Stanev EV, Al-Nadhairi R, Valle-Levinson A (2015) The role of density gradients on tidal asymmetries in the German Bight. Ocean Dyn 65:77–92. https://doi.org/10.1007/s10236-014-0784-8
Stanev EV, Jacob B, Pein J (2019) German Bight estuaries: an inter-comparison on the basis of numerical modeling. Cont Shelf Res 174:48–65. https://doi.org/10.1016/j.csr.2019.01.001
Staneva J, Stanev EV, Wolff J-O, Badewien TH, Reuter R, Flemming B, Bartholomä A, Bolding K (2009) Hydrodynamics and sediment dynamics in the German Bight. A focus on observations and numerical modelling in the East Frisian Wadden Sea. Cont Shelf Res 29:302–319. https://doi.org/10.1016/j.csr.2008.01.006
Stive MJF, de Schipper MA, Luijendijk AP, Aarninkhof SGJ, van Gelder-Maas C, van Thiel de Vries JSM, de Vries S, Henriquez M, Marx S, Ranasinghe R (2013) A new alternative to saving our beaches from sea-level rise: the sand engine. J Coast Res 290:1001–1008. https://doi.org/10.2112/JCOASTRES-D-13-00070.1
Valerius J, Kösters F, Zeiler M (2015) Erfassung von Sedimentverteilungsmustern zur großräumigen Analyse der Sedimentdynamik auf dem Schelf der Deutschen Bucht. Die Küste 83:39–63
van der Wegen M (2013) Numerical modeling of the impact of sea level rise on tidal basin morphodynamics. J Geophys Res Earth Surf 118:447–460. https://doi.org/10.1002/jgrf.20034
van Goor MA, Zitman TJ, Wang ZB, Stive MJF (2003) Impact of sea-level rise on the morphological equilibrium state of tidal inlets. Mar Geol 202:211–227
van Ledden M, Wang Z-B, Winterwerp H, de Vriend H (2004) Sand–mud morphodynamics in a short tidal basin. Ocean Dyn 54:385–391
van Maanen B, Coco G, Bryan KR, Friedrichs CT (2013) Modeling the morphodynamic response of tidal embayments to sea-level rise. Ocean Dyn 63:1249–1262. https://doi.org/10.1007/s10236-013-0649-6
van Straaten LMJU, Kuenen PH (1957) Accumulation of fine grained sediments in the Dutch Wadden Sea. Geologie Mijnb 19:329–354
van Thienen-Visser K, Breunese JN, Muntendam-Bos AG (2015) Subsidence due to gas production in the Wadden Sea: how to ensure no harm will be done to nature. American Rock Mechanics Association
Vriend D (1996) Mathematical modeling of meso-tidal barrier island coasts part I: empirical and semi-empirical models. In: Advances in coastal and ocean engineering, pp 115–149
Wilkens J, Mayerle R (2005) Morphodynamic response to natural and anthropogenic influences in the Dithmarschen Bight. Die Küste 69:311–337
Zeiler M, Schulz-Ohlberg J, Figge K (2000) Mobile sand deposits and shoreface sediment dynamics in the inner German Bight (North Sea). Mar Geol 170:363–380
Zeiler M, Milbradt P, Plüß A, Valerius J (2014) Modelling large scale sediment transport in the German Bight (North Sea). Die Küste 81:369–392
Zijl F, Verlaan M, Gerritsen H (2013) Improved water-level forecasting for the Northwest European Shelf and North Sea through direct modelling of tide, surge and non-linear interaction. Ocean Dyn 63:823–847. https://doi.org/10.1007/s10236-013-0624-2
Zijl F, Sumihar J, Verlaan M (2015) Application of data assimilation for improved operational water level forecasting on the northwest European shelf and North Sea. Ocean Dyn 65:1699–1716. https://doi.org/10.1007/s10236-015-0898-7
Acknowledgements
This work has been carried out within the framework of the Network of Experts (BMVI-Expertennetzwerk) financed by the German Federal Ministry of Transport and Digital Infrastructure. We thank all our co-workers at the Federal Waterways Engineering and Research Institute (BAW) in Hamburg for their continuous support. Tara Mahavadi is thanked for simulations with alternative bathymetric scenarios used for comparison with the bathymetric scenario presented in this study. Fruitful discussions with Norbert Winkel, Günther Lang, and Elisabeth Rudolph are thankfully acknowledged. We are deeply grateful to the two anonymous reviewers as well as to the editor for their valuable comments which helped to significantly improve our manuscript.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Responsible Editor: Emil Vassilev Stanev
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wachler, B., Seiffert, R., Rasquin, C. et al. Tidal response to sea level rise and bathymetric changes in the German Wadden Sea. Ocean Dynamics 70, 1033–1052 (2020). https://doi.org/10.1007/s10236-020-01383-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10236-020-01383-3