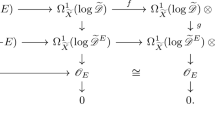Abstract
Let X be a projective variety. If L is a line bundle on X, for each positive integer m in \({\mathbf {N}}(L)=\{m\in {\mathbb {N}}\mid H^0(X,L^{\otimes m})\ne 0\}\), the global sections of \(L^{\otimes m}\) define a rational map
where \(Y_m\) is the closure of \(\phi _m(X)\). It is well-known that for all sufficiently large \(m\in {\mathbf {N}}(L)\), the rational maps \(\phi _m:X\dashrightarrow Y_m\) are birationally equivalent to a fixed fibration (the Iitaka fibration), and \(\kappa (L):=\dim Y_m\) is called the Iitaka dimension of L. In a recent paper titled “Iitaka fibrations for vector bundles”, Mistretta and Urbinati generalized this to a vector bundle E on X. Let \({\mathbf {N}}(E)\) be the set of positive integers m such that the evaluation map \(H^0(X,S^m E)\rightarrow S^m E_x\) is surjective for all points x in some nonempty open subset of X. For each \(m\in {\mathbf {N}}(E)\), the global sections of \(S^m E\) define a rational map
where \({\mathbb {G}}(H^0(X,S^m E),{{\mathrm{rank}}}S^m E)\) is the Grassmannian of \({{\mathrm{rank}}}S^m E\)-dimensional quotients of \(H^0(X,S^m E)\). Mistretta and Urbinati showed that for every \(m\in {\mathbf {N}}(E)\), the rational maps \(\varphi _{km}\) are birationally equivalent for sufficiently large k, and called \(\kappa (E):=\dim Y_{km}\) the Iitaka dimension of E. Here we first slightly improve Mistretta and Urbinati’s result to show that the rational maps \(\varphi _{m}\) are birationally equivalent for all sufficiently large \(m\in {\mathbf {N}}(E)\). Then we show that
An immediate corollary of this inequality is that if E is big then \(\kappa (E)=\dim X\), which answers a question of Mistretta and Urbinati. Another corollary is that if E is big then \(\det E\) is big, provided that \({\mathbf {N}}(E)\ne \emptyset \).
Similar content being viewed by others
1 Introduction
Notations and conventions We will work over an algebraically closed field. Varieties are assumed to be irreducible. Points of a variety mean closed points. If V is a vector space, \({\mathbb {P}}(V)\) denotes the projective space of one-dimensional quotients of V, and \({\mathbb {G}}(V,r)\) denotes the Grassmannian of r-dimensional quotients of V. If E is a vector bundle on a variety X and \(x\in X\) is a point, we denote by \({\mathbb {P}}(E)\) the projective bundle of one-dimensional quotients of E, and by \(E_x\) the fiber of E over x (not the stalk of the germs of sections of E at x).
Let X be a projective variety. It is a basic construction in algebraic geometry that a line bundle L on X such that \(H^0(X,L^{\otimes m})\ne 0\) for some \(m>0\) naturally induces a rational map from X to the projective space \({\mathbb {P}}\bigl (H^0(X,L^{\otimes m})\bigr )\). In [2], Mistretta and Urbinati studied a generalization of this construction to vector bundles as follows.
Definition 1
Let E be a vector bundle on a projective variety X, and let U be an open subset of X. We say that
-
(1)
E is globally generated on U if the evaluation map \(H^0(X,E)\rightarrow E_x\) is surjective for every point \(x\in U\).
-
(2)
E is generically generated if it is globally generated on some nonempty open subset of X.
-
(3)
E is asymptotically generically generated (AGG) if for some positive integer m, the mth symmetric power \(S^m E\) of E is generically generated.
Definition 2
Let E be an AGG vector bundle of rank r on a projective variety X. Let m be a positive integer such that \(S^m E\) is globally generated on a nonempty open subset \(U\subseteq X\). Denote
Then one can define a rational map
by sending a point \(x\in U\) to the \(\sigma _m(r)\)-dimensional quotient \([H^0(X,S^m E)\twoheadrightarrow S^m E_x]\) of \(H^0(X,S^m E)\) under the evaluation map. We call \(\varphi _m\) the mth Kodaira map of E.
Our first result is a slight improvement on [2, Theorem 4.4].
Theorem 3
Let E be an AGG vector bundle on a complex projective variety X, and denote
For each \(m\in {\mathbf {N}}(E)\), let \(\varphi _m\) be the mth Kodaira map of E, and let \(Y_m\) be the closure of \(\varphi _m(X)\). Then for all sufficiently large \(m\in {\mathbf {N}}(E)\), the rational maps \(\varphi _{m}:X\dashrightarrow Y_{m}\) are birationally equivalent to a fixed surjective morphism of projective varieties
That is, there exists a commutative diagram

where the horizontal maps are birational and \(u_{\mathbb {G}}\) is a morphism.
The statement in [2, Theorem 4.4] is the same except that instead of “for all sufficiently large \(m\in {\mathbf {N}}(E)\)”, they have “for every \(m\in {\mathbf {N}}(E)\) and for \(k\gg 0\)” the rational maps \(\varphi _{km}:X\dashrightarrow Y_{km}\) are birationally equivalent to a fixed surjective morphism \(\varphi _{\mathbb {G}}:X_{\mathbb {G}}\rightarrow Y_{\mathbb {G}}\). Our version is more in line with the original Iitaka fibrations for line bundles [1, Theorem 2.1.33]. We also remark that compared to the case of line bundles, the difficulty in the proof comes from the fact that for a vector bundle E, \(S^p E\otimes S^q E\) is not isomorphic to \(S^{p+q}E\), and also that the morphism \(\varphi _{\mathbb {G}}:X_{\mathbb {G}}\rightarrow Y_{\mathbb {G}}\) is in general not a fibration (i.e., may not have connected fibers: see [2, Example 3.7]).
Following [2], we call the dimension of \(Y_{\mathbb {G}}\) the Iitaka dimension of E, and denote it by \(\kappa (X,E)\) or \(\kappa (E)\). Mistretta and Urbinati showed that if E is strongly semiample, meaning that \(S^m E\) is globally generated on X for some \(m>0\), then \(\kappa (E)=\kappa (\det E)\) [2, Remark 4.5]. They then raised several questions on Iitaka dimensions for vector bundles which are not necessarily strongly semiample. Our second result, which is an inequality relating the Iitaka dimensions of E and \({\mathcal {O}}_{{\mathbb {P}}(E)}(1)\), can help answer some of those questions.
Theorem 4
Let E be an AGG vector bundle of rank r on a projective variety X. Let \(\pi :{\mathbb {P}}(E)\rightarrow X\) be the projective bundle of one-dimensional quotients of E, and let \({\mathcal {O}}_{{\mathbb {P}}(E)}(1)\) be the tautological quotient line bundle of \(\pi ^*E\) on \({\mathbb {P}}(E)\). Then
Corollary 5
Let E be an AGG vector bundle on a projective variety X. If E is big (meaning that \({\mathcal {O}}_{{\mathbb {P}}(E)}(1)\) is big), then \(\kappa (E)=\dim X\).
This answers Question 4.7 and 4.8 in [2].
Corollary 6
Let E be an AGG vector bundle on a projective variety X. If E is big, then \(\det E\) is big.
This answers Question 4.6 in [2] affirmatively when E is big. Note that Corollary 6 is interesting in its own right since it is false without the AGG assumption: for example let E be a direct sum of line bundles
Then E is big if and only if some nonnegative \({\mathbb {Z}}\)-linear combination of the \(D_i\) is big [1, Lemma 2.3.2], whereas \(\det E\) is big if and only if \(D_1+\cdots +D_r\) is big.
2 Proofs
Lemma 7
Let E be a vector bundle on a projective variety X. If p and q are positive integers such that \(S^p E\) and \(S^q E\) are globally generated on an open subset U of X, then \(S^{p+q} E\) is globally generated on U. Moreover, if \(x,y\in U\) are points such that \(\varphi _p(x)\ne \varphi _p(y)\), then \(\varphi _{p+q}(x)\ne \varphi _{p+q}(y)\).
Proof
By assumption the evaluation maps
are surjective for each \(x\in U\). It thus follows from the commutative diagram

that the evaluation map \(H^0(X,S^{p+q} E)\rightarrow S^{p+q} E_x\) is surjective. Hence \(S^{p+q} E\) is globally generated on U.
For each point \(x\in U\), by definition
If \(x,y\in U\) are points such that \(\varphi _p(x)\ne \varphi _p(y)\), then there exists an element v in \(H^0(X,S^p E)\) such that
Pick any \(w\in H^0(X,S^q E)\) such that
Denote by \(v\cdot w\in H^0(X,S^{p+q} E)\) the image of \(v\otimes w\in H^0(X,S^p E)\otimes H^0(X,S^q E)\) under the multiplication map. It follows from the commutative diagram above that
Hence \(\varphi _{p+q}(x)\ne \varphi _{p+q}(y)\). \(\square \)
Proof of Theorem 3
By the proof of [2, Theorem 4.4], for each \(m\in {\mathbf {N}}(E)\) the rational map \(\varphi _m:X\dashrightarrow Y_m\) factors through \(\varphi '_{\mathbb {G}}=\varphi _{\mathbb {G}}\circ u_{\mathbb {G}}^{-1}:X\dashrightarrow Y_{\mathbb {G}}\). So to show that \(\varphi _m=\varphi '_{\mathbb {G}}\) for sufficiently large m, it is enough to show that \(\varphi '_{\mathbb {G}}(x)\ne \varphi '_{\mathbb {G}}(y)\) implies \(\varphi _m(x)\ne \varphi _m(y)\) for all points x and y in some nonempty open subset of X.
Pick \(m_1,\ldots ,m_n\in {\mathbf {N}}(E)\) which generate \({\mathbf {N}}(E)\) as a semigroup. By [2, Theorem 4.4], \(\varphi _{km_i}=\varphi '_{\mathbb {G}}\) for \(k\gg 0\). Hence all sufficiently large \(m\in {\mathbf {N}}(E)\) can be written as \(m=\sum _{i=1}^{n} k_im_i\), where \(k_i\in {\mathbb {N}}\) and at least one of \(\varphi _{k_im_i}=\varphi '_{\mathbb {G}}\). It thus follows from Lemma 7 that \(\varphi '_{\mathbb {G}}(x)\ne \varphi '_{\mathbb {G}}(y)\) implies \(\varphi _m(x)\ne \varphi _m(y)\). \(\square \)
Proof of Theorem 4
Let \(m>0\) be a positive integer such that \(S^m E\) is globally generated on a nonempty open subset U of X. We denote
Let \(Q_m\) be the tautological quotient bundle on \({\mathbb {G}}_m\). Then \({\mathbb {P}}(Q_m)\) is isomorphic to a two-step flag variety
so there are projection morphisms
Let \(x\in U\) be a point. Then the evaluation map \(H^0(X,S^m E)\twoheadrightarrow S^m E_x\) is surjective. By definition a point \(y\in \pi ^{-1}(x)\) is a one-dimensional quotient \([E_x\twoheadrightarrow L]\) of \(E_x\). Since
the line bundle \({\mathcal {O}}_{{\mathbb {P}}(E)}(m)\) is globally generated on the open set \({\widetilde{U}}=\pi ^{-1}(U)\subseteq {\mathbb {P}}(E)\). Let
be the morphism defined by the global sections of \({\mathcal {O}}_{{\mathbb {P}}(E)}(m)\) on \({\mathbb {P}}(E)\), and let
Then there is a commutative diagram

For each point \(x\in U\),
and
is the mth Veronese embedding. Hence
Since \(\dim \varphi _m(U)=\kappa (X,E)\) and \(\dim \phi _m({\widetilde{U}})=\kappa \bigl ({\mathbb {P}}(E),{\mathcal {O}}_{{\mathbb {P}}(E)}(1)\bigr )\) for sufficiently large \(m\in {\mathbf {N}}(E)\),
\(\square \)
Corollary 5 follows immediately from Theorem 4. As for Corollary 6, applying the argument in the proof of [2, Theorem 3.4] to an open set \(U\subseteq X\) where \(S^m E\) is globally generated, one sees that the rational map \(\varphi _{\mathbb {G}}:X\dashrightarrow Y_{\mathbb {G}}\) is a composition of the Iitaka fibration \(\varphi _{\det E}:X\dashrightarrow Y_{\infty }\) followed by a dominant rational map \(Y_{\infty }\dashrightarrow Y_{\mathbb {G}}\). It follows that
If E is big (and AGG), \(\kappa (E)=\dim X\) by Corollary 5, and hence \(\kappa (\det E)=\dim X\).
References
Lazarsfeld, R.: Positivity in Algebraic Geometry I–II, Ergeb. Math. Grenzgeb, vols. 48–49. Springer, Berlin (2004)
Mistretta, E., Urbinati, S.: Iitaka fibrations for vector bundles, IMRN, rnx239. https://doi.org/10.1093/imrn/rnx239
Acknowledgements
The author gratefully acknowledges the support of MoST (Ministry of Science and Technology, Taiwan).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jow, SY. Iitaka dimensions of vector bundles. Annali di Matematica 197, 1631–1635 (2018). https://doi.org/10.1007/s10231-018-0740-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-018-0740-1