Abstract
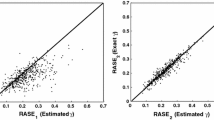
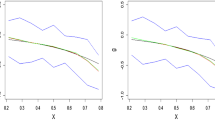
In this paper, multivariate partially linear model with error in the explanatory variable of nonparametric part, where the response variable is m dimensional, is considered. By modification of local-likelihood method, an estimator of parametric part is driven. Moreover, the asymptotic normality of the generalized least square estimator of the parametric component is investigated when the error distribution function is either ordinarily smooth or super smooth. Applications in the Engel curves are discussed and through Monte Carlo experiments performances of \(\hat{\beta }_{n}\) are investigated.


Similar content being viewed by others
References
Blundell, R., Duncan, A., Pendakur, K.: Semiparametric estimation of consumer demand. J. Appl. Econom. 13, 435–461 (1998). https://doi.org/10.1002/(SICI)1099-1255(1998090)13:5%3c435::AID-JAE506%3e3.0.CO;2-K
Fan, J., Masry, E.: Multivariate regression estimation with errors-in-variables: asymptotic normality for mixing processes. J. Multivar. Anal. 43, 237–271 (1992). https://doi.org/10.1016/0047-259X(92)90036-F
Fan, J., Truong, Y.K.: Nonparametric regression with errors in variables. Ann. Stat. 21, 1900–1925 (1993)
Fuller, W.A.: Measurement Error Models. Wiley, New York (1987)
Liang, H.: Asymptotic normality of parametric part in partially linear model with measurement error in the non-parametric part. J. Stat. Plann. Inference 86, 51–62 (2000). https://doi.org/10.1016/S0378-3758(99)00093-2
Lopez, B.P., Manteiga, W.G.: Multivariate partially linear model. Stat. Probab. Lett. 76, 1543–1549 (2006). https://doi.org/10.1016/j.spl.2006.03.016
Masry, E.: Multivariate probability density deconvolution for stationary random processes. IEEE Trans. Inform. Theory 37, 1105–1115 (1991). https://doi.org/10.1109/18.87002
Masry, E.: Asymptotic normality for deconvolution estimators of multivariate densities of stationary processes. J. Multivar. Anal. 44, 47–68 (1993a). https://doi.org/10.1006/jmva.1993.1003
Masry, E.: Strong consistency and rates for deconvolution of multivariate densities of stationary processes. Stoch. Process. Appl. 47, 53–74 (1993b). https://doi.org/10.1016/0304-4149(93)90094-K
Masry, E.: Multivariate regression estimation with errors in variables for stationary processes. Nonparametr. Statist. 3, 13–36 (1993c). https://doi.org/10.1080/10485259308832569
Phlips, L.: Applied Consumption Analysis. North-Holland, Amsterdam (1974)
Robinson, P.: Root-N-consistent semiparametric regression. Econometrica 56, 931–954 (1988). https://doi.org/10.2307/1912705
Toprak, S.: Semiparametric regression models with errors in variables. PhD Thesis. Dicle University, Diyarbakir (2015). https://tez.yok.gov.tr/UlusalTezMerkezi/tezSorguSonucYeni.jsp
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The following lemmas are needed to prove Theorem 1. For the proof of the lemmas, the reader is referred to Liang (2000).
Lemma 1
Let \( V_{1},\ldots ,V_{n} \) be independent random variables with 0 mean and there is \(\delta \ge 0\) for \(E\vert V_{ik}\vert ^{2+\delta }\le C<\infty \). Assume \(\left\{ a_{ji},i,j=1,\ldots ,n\right\} \) be a sequence of positive numbers such that \( \sup _{i,j\le n}\vert a_{ji}\vert \le n^{-p_{1}} \) for some \( 0<p_{1}<1 \) and \( \sum _{j=1}^{n}a_{ji}=O\left( n^{p_{2}}\right) \) for \( p_{2}\ge \max \left( 0,2/\left( 2+\delta \right) -p_{1}\right) \). Then
Lemma 2
Suppose that Assumptions 1.1 and 1.3 hold. Then
where \(G_0\left( .\right) =g\left( .\right) \) and \(G_l\left( .\right) =\gamma _l\left( .\right) \) for \(l=1,\ldots ,p\).
Lemma 3
Suppose that Assumptions 1.1–1.5 hold. Then
where \( \mathbf B \) is given in Assumption 1.1.
Proof of the Theorem
Then
Lemma 3 gives that \(n\left[ I_{m}\otimes \left( \widetilde{\varvec{X}}^\mathrm{T}\widetilde{\varvec{X}} \right) ^{-1}\right] \) converges to \( \mathbf B ^{-1} \). Hence, we need to show that \( \frac{1}{\sqrt{n}}\left[ I_{m}\otimes \widetilde{\varvec{X}}^\mathrm{T}\right] \text {vec}\left( \widetilde{\varvec{G}}\right) \) and \( \frac{1}{\sqrt{n}}\left[ I_{m}\otimes \widetilde{\varvec{X}}^\mathrm{T}\left( \varvec{ I-\omega }\left( T\right) \right) \right] \text {vec}\left( \varvec{\varepsilon }\right) \) converge in probability to zero.
Consider the matrix \(\frac{1}{\sqrt{n}}\widetilde{\varvec{X}}^\mathrm{T} \widetilde{\varvec{G}}\). Its krth element is
If we take \(\delta =0, V_j=V_k\), \(a_{ji}=\widetilde{g}_r\), \(1/4 \le p_1 \le 1/3, p_2=1-p_1\) in Lemma 1, then
Using Abel’s inequality \(\left| \widetilde{\varvec{\gamma }}_k^\mathrm{T}\widetilde{g}_r \right| \le n \max _{i\le n}\left| \widetilde{g}_r\right| \max _{i\le n}\left| \widetilde{\varvec{\gamma }}_k\right| \). Taking \( G_{0}=g_{r} \) and \( G_{j}=\varvec{\gamma }_k \) in Lemma 2 one gets
and
This means
If we take \(\delta =1, V_j=V_{k}\), \(a_{ji}=\omega _{n,h}\left( T_{i},T_{j} \right) ,p_1=2/3, p_2=0\) in Lemma 1, we obtain
Using Abel’s inequality and Eqs. (11) and (13)
All these means that \( \frac{1}{\sqrt{n}}\left[ I_{m}\otimes \widetilde{\varvec{X}}^\mathrm{T}\right] \text {vec}\left( \widetilde{\varvec{G}}\right) \) is \(o\left( 1\right) \).
For a given arbitrary fixed vector \(\mathbf a \in \mathbb {R}^{pm}/\left\{ 0\right\} \) to show that
let \(\mathbf c ^\mathrm{T}=\mathbf a ^\mathrm{T}\left[ I_{m}\otimes \widetilde{\varvec{X}}^\mathrm{T}\left( \varvec{ I-\omega }\left( T\right) \right) \right] \). Note that \(\mathbf c ^\mathrm{T}=\left( \mathbf c ^\mathrm{T}_1,\ldots ,\mathbf c ^\mathrm{T}_m\right) \), where \(\mathbf c ^\mathrm{T}_r=\left( c_{r1},\ldots ,c_{rn}\right) \).
where \(\mathbf o ^\mathrm{T}_i=\left( c_{1i},\ldots ,c_{mi}\right) \). Using the assumption that the error vectors \(\mathbf e _i\) are independent variables with mean vector 0 and matrix of variances and covariances \(\varvec{\varSigma }=\sigma _{rs}\) where \(r,s=1,\ldots ,m\) we have \(E\left( \mathbf o ^\mathrm{T}_i\mathbf e _i\right) =0\) and \(Var\left( \mathbf o ^\mathrm{T}_i\mathbf e _i\right) =\mathbf o ^\mathrm{T}_i\varvec{\varSigma }{} \mathbf o _i\).
Using Lemma 3, \(n^{-1}{} \mathbf a ^\mathrm{T}\left[ \varvec{\varSigma }\otimes \widetilde{\varvec{X}}^\mathrm{T}\left( \varvec{ I-\omega }\left( T\right) \right) \left( \varvec{ I-\omega }\left( T\right) \right) ^\mathrm{T}\widetilde{\varvec{X}}\right] \mathbf a \rightarrow \mathbf a ^\mathrm{T}\left[ \varvec{\varSigma }\otimes \varvec{B}\right] \mathbf a \). From Lindeberg condition, we need to show that
Hence, if we show that \(\max _{1\le i\le n}Var\left( \mathbf o ^\mathrm{T}_i\mathbf e _i\right) =o(n)\), then Eq. (15) will hold. Let \(b_r\in \mathbb {R}^{m} \) be the vector where all components are 0 except the rth component, which is 1.
where \(k_r=\left( b^\mathrm{T}_r \otimes \mathbf I _p\right) \mathbf a \in \mathbb {R}^{p}\).
From Assumption 1.5, \(\left\| \varvec{\omega }\left( T\right) ^\mathrm{T}\right\| _{\infty }\) is uniformly bounded. By assumption of theorem, \(E\left| \mathbf V _{ik}\right| ^{2+\delta }\le C <\infty \) for \(\delta \ge 0\) and all i and k. Using Markov inequality
for any constant \(m_n\).
If we take \(m_n=n^{1/2}\log n\), then
This means that \(\left\| \varvec{V}_{k}\right\| _\infty =o_p(n^{1/2})\) holds.
Using Eqs. (12) and (13), we get \(\left\| \widetilde{\varvec{\gamma }}k_r\right\| _{\infty }=o(1)\) and \(\left\| \varvec{\omega }\left( T\right) \varvec{V}k_r\right\| _{\infty }=O\left( n^{-1/3}\log n\right) \), respectively.
Hence, by Cramer–Wold device we have
Rights and permissions
About this article
Cite this article
Yalaz, S. Multivariate partially linear regression in the presence of measurement error. AStA Adv Stat Anal 103, 123–135 (2019). https://doi.org/10.1007/s10182-018-0326-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10182-018-0326-7