1 Introduction

Predictions suggest that demand for the European airspace will grow by a factor of 1.5 between 2012 and 2035 (SESAR 2015). Unless procedural, automation, or infrastructure changes are utilized to mitigate the effects of this growth, it will inevitably add to congestion at major airports, which may in turn lead to increased fuel consumption, emissions, and delays (Simaiakis and Balakrishnan 2010; Simaiakis et al. 2012). Increased usage of airport resources will also heighten demand on those involved in surface operations management, particularly tower controllers, who direct aircraft among stands, taxiways, holding areas, and runways. Controllers consider flight schedules, system disruptions, safety requirements, and pushback and taxi times for individual aircraft, among other aspects, to attempt to make the most effective use of airport capacity (National Research Council 1997). Capacity is limited by the number and availability of terminals, apron stands, taxiways, and runways, and as such, effective allocation of such resources can impact system throughput and profitability (Pellegrini and Rodriguez 2013). Bottlenecks at runways, taxiways, and other ground-based infrastructure can limit system performance, but decision support systems (DSS) that provide optimal scheduling and routing guidance may help to alleviate this (Karisch et al. 2012). Effective interaction between human operators and decision support technology affects efficiency within operational environments, and as such, developing a deeper understanding of human behavior during optimization problem solving may add value to the development of DSS in joint-cognitive systems (Kefalidou 2017; MacGregor and Ormerod 1996). While there is a considerable foundation of work focused on air traffic control relating to topics including, but not limited to, workload (Ahlstrom 2007; Corradini and Cacciari 2002), situation awareness (Edwards et al. 2016; Friedrich et al. 2018; van de Merwe et al. 2012), and decision-making behavior (Corver and Grote 2016; Karikawa et al. 2014), factors influencing performance and strategies employed by humans engaged specifically in optimization problem solving are less understood (Kefalidou and Ormerod 2014). This work seeks to enhance the body of knowledge related to human behavior and performance in vehicle routing optimization tasks as practiced in for tower control applications.

Aircraft routing is an example of a combinatorial optimization problem, a problem type found in many real-world domains where resource allocation is critical, including air traffic control (Stergianos et al. 2015), shipping and transportation (Crainic et al. 2009; Zäpfel and Wasner 2002), and manufacturing (Rambau and Schwarz 2014; Venkateshan et al. 2008). As implied by the name “combinatorial,” such problems can consist of solving combinations of choices, and the complexity is often in the interaction of the elements. An example of such a problem is the classical “traveling salesman problem” (TSP), which involves finding the order in which to visit a set of cities, where there is a known travel distance (or cost/time) between each pair of cities, such that the total distance travelled is minimized. The problem solver has to make a combination of decisions about which city the salesman should visit next. In airports, examples of this type of problem include selecting paths for aircraft to taxi around an airport, allocating aircraft to parking stands, or deciding on a takeoff sequence, as will be considered in this paper. In airport domains, mathematical optimization techniques have already provided insight into scheduling of departures (Atkin 2008; De Maere et al. 2017; Stergianos et al. 2016), arrivals (Beasley et al. 2000, 2004; Stergianos et al. 2015), and ground movement (Atkin et al. 2010b; Weiszer et al. 2014). While humans have demonstrated the ability to solve relatively large combinatorial optimization problems, performance diminishes as problems increase in complexity (Kefalidou 2017).

In order to leverage the benefits of DSS, designs must consider both functional and sociotechnical requirements in order to allocate functions effectively between human and computer agents. The objective of this research was to explore some of the human aspects of this topic, specifically relating to factors influencing human performance associated with solving vehicle routing optimization problems in a task representative of ground movement control within airports. First, we discuss the motivation behind this work and present a review of current understanding of air traffic control and human performance while solving combinatorial optimization problems. We then describe the outcomes from an investigation into human performance and strategies employed in a spatial–temporal problem-solving task, which was presented in the form of an airport ground movement management game. We address the current gap in the knowledge related to how people solve routing problems involving the spatial and temporal dimensions and multiple vehicles without prescribed guidance, with a view to utilizing this knowledge to improve airport DSS outcomes: by improving human decision-making performance, improving the interaction between the operator and the system, or developing new ways for operators to better utilize DSS feedback.

2 Problem identification

This work is motivated by an ongoing collaboration with NATS who perform the air traffic control operations at London Heathrow Airport, a major international airport in the UK. Members of the research team began working with NATS at Heathrow in 2003, studying the roles of the tower controllers and the airport’s operational constraints while also considering the potential for automation of elements of the problem space. This partnership has resulted in various models and algorithms for managing airport processes at Heathrow and elsewhere (e.g., runway sequencing (Atkin 2008; Atkin et al. 2008; De Maere et al. 2017) and ground movement (Ravizza 2013; Stergianos et al. 2015, 2016), and has resulted in a live system running at Heathrow for predicting takeoff times and assigning aircraft pushback times (Atkin et al. 2010a, 2013). At Heathrow, ground movement control is divided into two separate roles: the ground controller manages aircraft routing around the taxiways between stands and runway queues, while the runway controller manages the routing of aircraft within the holding areas near to the runways, where aircraft queue while awaiting takeoff. At the interface of these areas, flights are handed off from one role to the other.

We often think of flights as being highly constrained by a schedule, but in fact, multiple time windows often apply to different operations and there is usually a little flexibility in timings to account for unexpected delays and variable unloading, preparation, and loading times. Flight schedules consider the times at which aircraft leave the stands and set off along the taxiways. Indeed, on-time performance is often measured in terms of these timings—how many aircraft left the stand within 15 min of the target time. These times are derived from a flight schedule determined by an airline in order to maximize revenue and/or on-time performance (i.e., ensuring that the timings will be achievable). Schedules specify when each aircraft will takeoff and land at each airport, and they consider the interactions between aircraft and crews. However, there are also other time windows which are at least as important from an air traffic controller’s point of view. For example, in the European airspace, a central flow management unit considers all of the suggested flight schedules for the different aircraft traveling through busy air sectors. Using this information, the central flow management unit predicts the load at different sectors and at different times and attempts to limit the load in such sectors by delaying the takeoffs of some aircraft elsewhere at busy times so that they arrive at these sectors at a less busy time. This is vital for ensuring that the workload for the controllers of these sectors is manageable and safe. These calculated takeoff times (CTOTs) apply 15-min windows for aircraft to takeoffs rather than enforcing an exact time (from − 5 to + 10 min of the allocated time), which allows for a significant amount of resequencing of aircraft. As such, tower controllers are given agency over making decisions regarding the departure sequence and route that the aircraft takes between the stand, taxiway, and runway. This flexibility offers many potential benefits related to delay reductions and operational efficiency improvements, but it also increases the decision-making challenge placed on controllers.

Previous research has shown that tower controllers face challenges related to routing aircraft efficiently, sequencing flights at the runway, and maintaining situation awareness (Atkin 2008). Observational methods have revealed that individual differences exist among controller routing and sequencing strategies, with controllers holding preferences for certain routes through the airfield (Atkin 2008). Furthermore, the runway sequence is itself dynamic in nature, where runway controllers are frequently required to direct aircraft to overtake one another on taxiways and within holding areas to maintain an ideal departure sequence. While the role of the air traffic controller and factors influencing their performance have a well-grounded foundation in the research literature, human behavior during tasks involving optimization problem solving has received a lesser degree of attention. A better understanding of such phenomena could lead to improvements in the user-centered design of decision support tools (Kefalidou 2017). We argue that this aspect of the role is not sufficiently understood, particularly when applied to tower control operations, and as such, we sought to explore factors influencing human vehicle routing problem solving with an experimental approach.

3 Related work

3.1 The Role of the Air Traffic Controller

Air traffic control (ATC) encompasses several roles spanning different segments of a flight’s timeline (Durso and Manning 2008). At major airports like Heathrow, the tower control role may be further divided into two responsibilities: ground movement controllers and runway controllers (National Research Council 1997). The air traffic controller’s work has been examined previously in the human factors literature; for a thorough review of the role, we refer the reader to Durso and Manning (2008) and to the National Research Council (1997). Research has primarily explored the work requirements of en route controllers, or those who direct traffic on the portion of the flight path outside aerodrome operations (Della Rocco et al. 1990; Endsley and Rodgers 1994; Inoue et al. 2012), but fewer have examined decision making and problem solving encountered in tower control.

It is widely recognized that limiting factors on human capacity in air traffic control include mental workload (Ball et al. 2007; Hillburn 2004) and situation awareness (Endsley and Rodgers 1994; Friedrich et al. 2018). Situation awareness (SA) is also considered to be a critical component of air traffic control operations (Bekier et al. 2012; Della Rocco et al. 1990; Endsley and Rodgers 1994). SA has been defined as “the perception of the elements in the environment within a volume of time and space, the comprehension of their meaning, and the projection of their status in the near future” (Endsley 1995). SA has also been considered as a construct representing directed attention (Smith and Hancock 1995) and alternatively, as a way to discuss distributed cognition in sociotechnical systems (Chiappe et al. 2012; Stanton et al. 2009). In order to expedite travel through an airport or airspace, controllers must be able to balance multiple demands, including communicating with flight crew and other operational staff, reviewing flight schedules, monitoring navigation and positioning data, and managing mental workload while also ensuring safe operations (Lindeis 2010). Friedrich et al. (2018) observed that increasing levels of task load negatively affected controller situation awareness and information scanning strategies when performing control tasks.

Managing workload is critical to the tower control function and can be considered as “the total cognitive effort an operator must exert to perform a task” (Ahlstrom 2007). Workload is a function of task requirements, environmental factors, and individual factors (Hart and Staveland 1988). In air traffic control, it is commonly thought that workload is affected by system complexity, particularly with respect to airspace design and traffic requirements (Durso and Manning 2008; Hillburn 2004). Decision support automation has the potential to support to controllers in maintaining their SA and managing workload, but to be most effective, designs must consider the appropriate level of automation for each task (Kaber and Endsley 1997). In an investigation of the relationship among automation usage, workload, and situation awareness during a conflict detection task, Edwards et al. (2017) observed that task performance varied as workload, SA, and the level of support that the automation provided varied. While the role of the air traffic controller and factors influencing their performance have a strong foundation in the research literature, human behavior during tasks involving optimization problem solving has received less attention, and yet could lead to improvements in the user-centered design of decision support tools (Kefalidou 2017).

3.2 Solution approaches to the tower control problem

Over the years, technology has offered innovative solutions for supporting the work of air traffic controllers with en route and tower control tasks. Automated DSS are intended to support controllers in planning, monitoring, and control tasks and have been proposed in systems including, but not limited to, GO-SAFE (Cheng and Foyle 2002), the surface trajectory-based operations concept (Stelzer et al. 2011), and runway scheduling decision support (Atkin et al. 2008; De Maere et al. 2017). However, in order to be used effectively, DSS design should incorporate an understanding of user mental models (Beard et al. 2013) and should be implemented in accordance with an appropriate level of automation to allow for efficient allocation of functions between the technical system and the human controller (Kaber and Endsley 2004). Thus, reviewing the decision-making and problem-solving practices during optimization problem solving will support the human-centered development of novel tower control support tools.

Of particular relevance to tower control problem solving is a class of spatial combinatorial problems called vehicle routing problems (VRPs). VRPs involve routing vehicles to customers (traditionally for delivering and/or picking up goods) so all required customer visits are satisfied by some appropriate vehicle (Dantzig et al. 1954; Toth and Vigo 2002). The VRP could be considered as a multiple-salesman version of the TSP, discussed earlier, where each city has to be visited by some salesman and the questions are which cities to allocate to which salesmen as well as in what order to visit cities. Common variants of the problem include additional time windows for visits, capacity constraints, or sequencing requirements. In ground-based operations within airports, the VRP problem structure can be seen in the routing and scheduling tasks, where ground and runway controllers direct aircraft to and/or through a number of limited resources like stands, taxiways, holding area zones, and runways. Particularly at airports where operations approach capacity limits, identifying optimal resource allocations in a timely manner can have a considerable positive effect on overall system performance.

Mathematical research on these problems has resulted in various algorithmic methods for rapidly identifying either optimal solutions or acceptably good solutions (using heuristic algorithms, where the problem is too complex to solve exactly in limited time). These include variations on Dijkstra’s algorithm (Stergianos et al. 2015; Weiszer et al. 2014) and tabu search (Glover 1989). With especially large problems, even modern computational methods can take a significant amount of time to solve, which can be problematic in environments which require rapidly generated, real-time solutions. Heuristic approaches have long been used to resolve these computation time issues. Interestingly, human problem solvers have demonstrated the capability to identify near-optimal solutions to certain optimization problems in relatively short amounts of time (MacGregor and Ormerod 1996; MacGregor et al. 1999). By investigating human heuristics for approaching combinatorial problems and by identifying factors that positively affect performance, outcomes may provide insight into new methods for developing computational solutions, or for enhancing existing heuristic algorithms.

3.3 Optimization problem solving by humans

Understanding how human problem solvers approach complex spatial tasks can also provide insights into spatial cognition, which can, in turn, benefit human–system integration within optimization-based DSS (MacGregor et al. 1999). A number of studies have focused on understanding spatial cognition in the traveling salesman problem (MacGregor and Chu 2011; MacGregor and Ormerod 1996; MacGregor et al. 1999; Van Rooij et al. 2003). While several have demonstrated that humans can quickly generate near-optimal solutions in relatively short amounts of time (MacGregor and Ormerod 1996), opinions diverge on the mechanisms underpinning such performance.

An improved understanding of human cognition during problem solving not only advances theoretical frameworks but can also contribute to the development of novel algorithmic approaches. In a study on human problem-solving strategies, Kefalidou and Ormerod (2014) identified a set of heuristics used by participants solving capacitated vehicle routing problems (CVRPs), a variant on the VRP which includes capacity constraints. Participants manually solved four CVRPs, during which verbal and visual protocols were collected to assess strategic thinking. Route construction heuristics involved arithmetic methods (calculating, averaging, maximizing, and route balancing) and visuospatial methods (clustering, moving to the nearest neighbor, anchoring, and remainder consideration). Although participants varied strategic approach through the course of each individual problem, participants appeared to adopt a primary route construction preference, leaning either toward visuospatial methods or arithmetic methods.

In an additional study, Kefalidou (2017) evaluated the effects of feedback on human performance while solving CVRPs and found that participants who used a computer-based support system that provided feedback identified more optimal solutions than those completing the problem-solving exercise with paper and pencil. It was observed that the computer-based system altered the task environment, reducing the demand on the participant. This aligns with Newell and Simon (1972) problem-solving model, in which task environment determines the problem space, choice of procedural approach, and application. This finding supports the integration of immediate feedback during problem solving to improve human problem solving on CVRP tasks and may have also resulted in improved situation- and goal-awareness during the tasks. Kefalidou (2017) recommended that additional strategies and heuristics should be investigated alongside computational algorithms to aid in the development of DSS. Although the present experiment does not explicitly consider feedback in the research question, we address this important topic in the discussion and recommend its consideration in future work.

4 Method

4.1 Participants

Thirty adults, ages 18–55 years, were recruited via fortuitous sampling from the University of Nottingham and surrounding community (73% male, 27% female). Participants were not required to possess background experience in air traffic control. As such, none had prior experience with air traffic management, but 10% of the participants did have professional experience with optimization or resource allocation activities. Participants received a £10 voucher as compensation for their time during their involvement in the study.

4.2 Experimental design

The study took a two-factor approach with a game-based framework. The problem-solving tasks under evaluation were presented to participants in the form of two games which varied across map layout (between subjects) and objective (within subjects). The map layout factor was presented across two levels representing task complexity: Map A (Fig. 1) and Map B (Fig. 2). Participants were randomly assigned a map condition and were then asked to play two games corresponding to the two levels of the objective factor. The game objective differed in terms of task flexibility; under the order-based objective participants were instructed to have the aircraft cards take off in a specified order and in the fewest number of turns, while under the interval-based objective participants were given flexibility in terms of assigning a sequence but were instructed to minimize delay and number of turns. Presentation of objectives was randomly assigned.

Fig. 1
figure 1

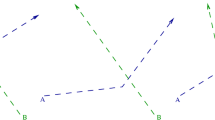
Map layout factor level A, based on a network graph developed by Atkin (2008)

Full size image
Fig. 2
figure 2

Map layout factor level B, based on a network graph developed by Atkin (2008)

Full size image

Performance and problem-solving strategies were assessed with quantitative and qualitative means. Quantitative-dependent variables related to participant performance, including a score based on each participant’s distance from the optimal solution and a score based on their compliance with the requested departure order. Additionally, participants provided subjective estimates of workload experienced under the varying conditions. In order to evaluate problem-solving heuristics and strategy formulation, the qualitative measures utilized think-aloud protocol data and video recordings of the gameplay.

4.3 Materials and equipment

4.3.1 Board game materials

The game employed two styles of game board, corresponding to the two map layout levels. Both network maps were based on layouts of two different holding area approaches to the runways at London Heathrow Airport in the UK. These maps were based on network graphs that were originally developed by Atkin (2008) and used in the development of optimization-based algorithms for runway scheduling and sequencing. The game framework was developed exclusively for use in the present study. The boards, shown in Figs. 1 and 2, consisted of a series of spaces (nodes), directional arrows, and the runway. Each map had two runway departure points but differed in number and arrangement of nodes. Participants assumed the role of a controller and were instructed to direct aircraft, represented as cards, through the network toward the runway where they could then “take off.” The goal of the game was to maximize compliance with the requested departure ordering condition while minimizing the total number of turns taken to complete the game.

Two variations of the game were developed for each map layout, based on semi-optimal runway schedules at the real-world airport. Each variation consisted of 27 aircraft cards, where each card displayed its flight code, weight class, and arrival time. Twenty-seven aircraft allowed for a realistic degree of task complexity, and the number was also considered to be achievable for participants to sequence within the timespan for each experimental session. For the participants assigned to the order-based objective condition, the cards also displayed its assigned departure slot; for example, the card labeled “Order: 1” was assigned to depart first, whereas the card labeled “Order: 3” was assigned to go third in line. Participants assigned to the interval-based objective condition, however, received a different set of instructions; instead, they were presented with a range of turn numbers in which the aircraft could take off without incurring delay. An example of the card data is presented in Table 1, which provides the details of one game associated with Board A.

Table 1 Card data associated with scenario A1, where departure order was presented during the order-based objective games and earliest/latest turn due dates were presented during the interval-based objective game
Full size table

4.3.2 Rules

Participants received training on the game’s goals and mechanics through verbal guidance and through an instructional document which participants reviewed. The turn-based game required participants to move cards through the network toward the runway. The game called for two actors: the adjudicator role, filled by the researcher, and the controller role, filled by each participant. In terms of mechanics, each turn had several phases.

At the beginning of each turn, the adjudicator would call out the new turn number (e.g., “it is now turn number four”) and then would check to see if any new aircraft were ready to enter the system. Any cards with an arrival date matching the current turn number would be made available to the controller by being placed beside the board. Once a card became available, the controller could move it immediately to an entry node on the board, but was also permitted to hold the card outside the network if they wished. Participants could move each card toward the runway, one node per turn, and was limited in terms of movement mechanics (e.g., only one card was allowed on each node at any given time). Upon arrival at the runway, participants could choose to have the card “take off” and be removed from the board. However, each aircraft card had a designated weight class, an indicator of the airplane’s size, which imposed restrictions on the temporal separation between two departures. For example, a heavy aircraft could depart in the next turn following a medium aircraft’s departure, but a medium aircraft was required to wait an additional turn following a heavy aircraft’s departure. This restriction was included to reflect real-world separation values imposed on airport departure scheduling by wake vortex separation constraints (Atkin 2008).

4.3.3 Data collection equipment

During gameplay, a Nikon Coolpix L340 20MP digital camera, mounted on a tripod, recorded audio and video. In addition, participants provided subjective estimates of workload by completing the paper-based raw NASA-Task Load IndeX (TLX) at the end of both variations of the game. The NASA-TLX is a widely used instrument for subjective workload assessment which captures participant perceptions of a range of physical and cognitive parameters (Hart and Staveland 1988). At the study’s completion, participants also filled out a debriefing survey which asked for information on demographics and background experience.

4.4 Procedure

Each experimental session began with the researcher explaining the purpose of the study, as well as the game’s goals, materials, rules, and mechanics to the participant. Participants were given an opportunity to ask questions, and game variations were designed to encourage a learning-through-playing approach. When the participant felt comfortable with the instructions, the first variant of the game began. Participants were encouraged to think aloud during gameplay, and they were occasionally probed for information about strategy, aircraft sequencing decisions, and prioritization. After all twenty-seven aircraft cards had departed from the runway, the game concluded and the participant completed the first NASA-TLX. Following this, the second variant began, presenting the game in the alternate objective condition from the first game. The researcher explained the new objective to the participants, and when they felt comfortable with the new goals, the second game began. At the conclusion, the participant completed the second NASA-TLX, followed by a debriefing survey.

4.5 Hypotheses

It was hypothesized that the problem-solving objective condition would affect task performance and workload. As the order-based objective specified a fixed sequence, thereby reducing the scale of the problem-solving task, it was anticipated that it would result in a lower level of mental workload and would likewise result in improved task performance. Similarly, it was hypothesized that the map layout factor would affect mental workload but not task performance; as the map layout factor represented task complexity, it was anticipated that the more complex map (B) would be associated with increased workload but that participants would be just as likely in both levels to identify optimal solutions.

5 Results and analysis

The thirty participants completed a total of fifty-nine games; although each participant played two games apiece, one participant did not complete the second scenario, and as such, only that participant’s first scenario was included in the analysis.

5.1 Performance metrics

5.1.1 Task performance

Games were formulated around a decision tradeoff framework, where the participants were instructed to navigate the aircraft cards to the runway in the fewest number of turns and in a specified sequence. The solutions that were considered optimal were those that minimized both game length and deviation from the requested sequence—a “delay” score. In the order-based objective problems, a score was calculated based on the number of aircraft that departed in their assigned slot. In the interval-based objective problems, aircraft were not assigned to specific slots, but participants were instead asked to have aircraft depart from the runway during a specific turn or turn interval; when aircraft departed past their latest due date, the number of turns by which they were delayed was added to the cumulative score.

Relatively few participants (n = 8) identified the optimal solution during the study. Of the fifty-nine games analyzed, eight were completed in the optimal number of turns and with the correct departure sequence. The majority of those optimally solved games (n = 7) occurred under the order-based objective games. Prior experience with non-ATC optimization concepts was inspected but did not appear to affect task performance. Indeed, of the three participants who declared having prior optimization experience in the debriefing survey, two identified the optimal solution to one game each, but not both. The six remaining optimal solutions were identified by six different participants with no prior professional-level experience with optimization.

The degree to which solutions satisfied the different objectives varied. For example, one participant solved a game in fewer turns than the optimal solution, but did so at the expense of a higher delay score. The participants assigned to the map A layout completed the games with an average of 2.57 turns (σ = 3.37) from the optimal solution in the order-based objective condition and an average of 2.00 turns (σ = 2.41) in the interval-based condition. The participants assigned to the map B layout completed the games in an average of 0.73 turns from the optimal solution (σ = 0.96) and 1.13 turns (σ = 1.30) from the optimal solution in the order-based and interval-based objectives, respectively. It is important to note that, due to the multi-objective nature of the problem-solving task, analyzing the number of turns taken to complete the game provides an incomplete view of task performance. Of the 23 games played that were not solved optimally in the order-based condition, 52% (n = 12) routed the aircraft in the correct sequence and within four turns of the optimal solution (Map A: µ = 3.27, σ = 6.08; Map B: µ = 1.45, σ = 2.16). Similarly, of the 26 suboptimal solutions to the interval-based games included in the analysis, 53% (n = 14) were completed within four turns of the optimal solution, with delay scores for suboptimal solutions ranging from 1 to 70 points (Map A: µ = 10.40, σ = 9.79; Map B: µ = 31.13, σ = 22.98).

5.1.2 Task duration

Task duration data were captured from the video recordings and were measured from the point at which the participant picked up the first card to the point where he or she removed the final card from the board. Due to technical issues, it was not possible to assess task duration accurately from several of the recordings, resulting in a sample of N = 53. Task duration was determined through statistical analysis to be distributed according to a 3-parameter Weibull distribution (shape = 2.061, scale = 18.66, threshold = 9.910) and had a mean value of 26.46 min (σ = 8.456). Although task duration was not a dependent variable of primary interest, it was captured in order to assess its relationship with task performance. A boxplot of task duration grouped by the independent variables is shown in Fig. 3.

Fig. 3
figure 3

Task duration by objective factor and map layout factor

Full size image

5.1.3 Logistic regression analysis

A logistic regression analysis identified a statistically significant relationship among task duration, the objective condition, and the likelihood of a participant producing an optimal solution to the game. Both the total task duration (p = 0.012) and the objective condition (p = 0.008) significantly affected the odds of a participant generating an optimal solution. As hypothesized, the map layout condition did not appear to have an effect on the likelihood of solution optimality (p = 0.901). Data did not appear to suffer from multicollinearity, and the Hosmer–Lemeshow test indicated that the model fits the data well, with equal variances between the fitted model and the null model (p = 0.784). The resulting regression equation is shown in Eq. (1).

$${\text{logit}}\left( {p\left( x \right)} \right) = \log \left( {\frac{p\left( x \right)}{1 - p\left( x \right)}} \right) = - 6.860 + 0.118x_{\text{TaskDuration}} + 2.570x_{\text{Objective}} + 0.113x_{\text{Map}}$$
(1)

where xobjective = 0 is the interval condition, = 1 is the order condition; xMap = 0 is map layout condition A, = 1 is map layout condition B.

The statistical significance of the task duration and objective factors demonstrates that both factors affected the likelihood of a participant producing an optimal solution to one of the game scenarios. Objective played a particularly strong role in affecting the odds ratio; the odds of a participant identifying an optimal solution when asked to complete the order-based objective was 13.13 times the odds of identifying an optimal solution to the interval-based objective (p = 0.008). Task duration also produced a significant effect on the odds ratio. For every additional minute spent solving the problem, the odds of producing an optimal solution increased 1.12 times (p = 0.012).

5.2 Behavior and strategic thinking

5.2.1 Challenges

Participants encountered a number of challenges during the game, primarily related to the game mechanics, but also with regard to the sequencing task. In terms of game mechanics, some participants required assistance with checking the validity of moves (e.g., whether or not they had already moved an aircraft card, or whether or not they were allowed to let an aircraft card depart from the board during a specific turn) and checking the turn number (a particular issue during the interval condition in which cards were due during a set of turns). Apart from mechanics, some participants experienced difficulty maintaining awareness over the current environmental state, which was associated with issues related to forgetting to move aircraft cards during a turn or blocking cards by moving later departures ahead in the queue too early. Interestingly, this reflects certain patterns observed in previous work with expert tower controllers which provided the motivation for this work; specifically, the novice participants who encountered issues with inadvertently blocking aircraft that were due to takeoff reflected the real-world challenge that controllers face of ensuring that taxiing aircraft do not block the movements of other aircraft (Atkin 2008).

5.2.2 Decisions and strategies

During each game, participants made choices related to route assignment, card sequencing, prioritization of cards, and departure timings. At the beginning of each turn as new aircraft became available for participants to add to the network, participants first selected an entry point and placement order. Entry point assignment strategy was primarily based on due date or order alone (e.g., cards with nearer due dates were often assigned to the shortest paths, and vice versa), but some participants also mentioned that aircraft weight, which affected departure sequencing, was considered prior to moving a card into the network.

In terms of timing, several participants sequenced aircraft upon arrival by queuing cards in sequence or in parallel across multiple queues. Other participants adopted a strategy in which they sequenced aircraft closer to the runway, selecting departures by choosing the best of what was available or by resequencing aircraft where the network layout allowed (primarily on the “A” board). The final group of participants employed a hybrid approach in which they placed aircraft in clusters of cards with similar due date or order requirements, but reordered cards into sequence where able as the cards progressed toward the runway. In addition to these methods, participants largely tended to assign priority to certain network paths; in both board conditions, it was observed that the majority of participants would select a single path as a primary queue, then would use a second distinct path as a route to insert cards into the sequence where needed, and would finally keep a third pathway relatively clear from cards to facilitate rapid movement when a latecomer would arrive on the board.

5.2.3 Situation awareness and resilience

Analysis of the video recordings and think-aloud protocol provided evidence of situation assessment and resiliency during gameplay. To varying degrees of success, participants completed each game scenario by applying a set of strategies. Table 2 contains a summary of the main routing heuristics observed during the analysis.

Table 2 Primary heuristics observed during the gameplay sessions relating to route construction
Full size table

Based on visual and verbal data gathered during the study, several heuristics were identified as being frequently used to maintain awareness during the routing and departure scheduling task. Heuristics aligned with the visuospatial and arithmetic-based categorization employed by Kefalidou and Ormerod (2014). During gameplay, participants demonstrated both types of approach to route construction. In the arithmetic-based routing heuristic, we observed strategies including calculating (participants counted out distances to determine adequacy of the route or planning several moves ahead), balancing (participants who attempted to spread the load across all major routes within the network), and maximizers (participants who assigned cards to routes depending on due date). In the visuospatial routing heuristic, we observed a large degree of nearest neighbor routing (sequential queuing) and clustering (grouping cards which were due within several turns of each other). An example of a participant practicing the balancing heuristic is shown in Fig. 4, and an example of a participant practicing the nearest neighbor heuristic is shown in Fig. 5. All participants employed a range of strategies throughout gameplay.

Fig. 4
figure 4

Demonstration of a balancing heuristic in which the participant spreads the load across the three primary routes to the runway

Full size image
Fig. 5
figure 5

Demonstration of routing a card with the nearest neighbor heuristic

Full size image

Each game was inherently a multi-objective optimization problem where participants attempted to minimize both game duration and deviations from order or due date. As such, several participants were able to plan ahead in a way that allowed them to build flexibility into their sequences; for example, several participants who solved the problems optimally on Board A practiced keeping the node immediately prior to the runway clear until the participant decided to move a card to the runway; this allowed them to resequence cards without blocking the runway if an unexpected circumstance arose. Queuing cards also appeared to reduce some of the burden of planning ahead; by queuing cards in direct sequence or by balancing them in near neighbor groupings across primary routes, the primary decision making occurred as cards entered the network, which meant that participants needed only to monitor the network for conflicts while moving cards toward the runway.

5.3 Workload estimates

At the end of each scenario, participants provided estimates of their perceived workload during the previous gameplay. The unweighted NASA-TLX provided insight into several aspects of workload most relevant to the game-based task. After removing incomplete questionnaires, twenty-seven participants’ questionnaires were included in the analysis. The six core aspects of workload were included in the evaluation, but four were viewed as most relevant to the task at hand: mental demand, performance, effort, and frustration level.

A Wilcoxon signed-rank test comparing workload in the order-based objective tasks versus the interval-based tasks revealed that the objective factor did not significantly affect mental demand (Z = 1.62, p = 0.10), effort (Z = 0.12, p = 0.91), frustration level (Z = 1.07, p = 0.29), or perceived level of performance (Z = 1.11, p = 0.27). Similarly, a series of Kruskal–Wallis tests indicated that the map layout factor did not significantly affect mental demand (H = 0.43, p = 0.51), effort (H = 0.16, p = 0.69), frustration level (H = 2.35, p = 0.12), or perceived performance level (H = 1.43, p = 0.23). Of the four parameters, participants reported experiencing relatively high levels of mental demand (µ = 69.3, σ = 15.9) and effort expenditure (µ = 67.6, σ = 17.0) with moderately low levels of frustration (µ = 38.2, σ = 22.5); however, perceptions of individual performance were also ranked moderately low (µ = 40.1, σ = 23.0). A summary of the results is shown in Fig. 6a, b with descriptive statistics in Table 3.

Fig. 6
figure 6

a Estimates of workload components given by participants under the Network Layout A condition, assessed via the NASA TLX instrument. b Estimates of workload components given by participants under the Network Layout B condition, assessed via the NASA TLX instrument (asterisks denote statistical outliers)

Full size image
Table 3 Workload descriptive statistics corresponding to Fig. 6a, b
Full size table

6 Discussion

The study of human behavior during optimization problem solving provides insight into decision making during these processes, which in turn can inform design choices for DSS for complex work environments. In the present work, the researchers used a game-based method to investigate strategies and factors affecting performance in an abstraction of an airport ground movement control task. Comparing solution quality among two alternative network layouts and two objective conditions, a logistic regression analysis revealed that the likelihood of a participant producing an optimal solution was affected by task duration and objective condition. Furthermore, analysis of think-aloud protocols and video recordings taken during each gameplay session suggested that participants who produced optimal and near-optimal solutions demonstrated planning behavior, an awareness of potential future conflicts between cards, and the ability to build in flexibility to enhance resilience to unexpected events.

Visuospatial and arithmetic heuristics were used for routing decisions, similar to CVRPs. This concurs with Kefalidou and Ormerod (2014) and Gigerenzer and Goldstein (1996) who found that optimization problem solvers employed fast and frugal heuristics to reduce workload during problem solving. Queue construction was very common, with approximately 85% of the participants engaging in the practice. It is possible that this reduced attentional demand. In practice, the majority of participants constructed queues in a semi-sequential or near-neighbor clustering pattern, with similar due dates or ordered cards grouped together. The queuing strategy in which cards were balanced across entry nodes and aligned behind near neighbors was the most frequently practiced. Verbal data analysis indicated that participants felt this allowed them to navigate individual cards more quickly through the network, and that it increased flexibility for resequencing when needed. We hypothesize that queuing in direct sequence or in near-neighbor clusters served to offload some cognitive demand imposed by the task requirements. This hypothesis is supported by Kefalidou and Ormerod (2014), who observed that visuospatial heuristics made use of the problem space and environment, and was more efficient than arithmetic heuristics in terms of demand.

In terms of navigation, the most frequently adopted strategy was to leave at least one route open in case of a late arrival needing to reach the runway rapidly. Interestingly, while strategies did not largely differ between optimal and suboptimal participants, there were several strategies almost exclusively demonstrated by participants with optimal solutions. Like the broader sample, optimal participants constructed queues by grouping cards in direct order or in near neighbor clusters. However, these participants were more likely to employ a hybrid sequencing approach, wherein cards would be sequenced upon entry into the network but would be resequenced as needed prior to the runway. Optimal participants also exhibited planning and future thinking more often than the rest of the sample, as evidenced through video and verbal records. This effort to maintain awareness allowed these participants to preempt conflicts between aircraft and ensure the optimal departure sequence and timing.

Predictors of optimal performance included an increased task duration and the type of objective. It is not surprising that participants who spent more time analyzing the problem and task environment were more likely to identify an optimal solution, but it is interesting to consider the differences in performance based on objective condition. The logistic regression analysis indicated that participants completing the game scenarios with the order-based objective were more likely to perform the task optimally than when playing the interval-based objective game. At first blush, one might think that performance would improve in the interval-based games due to the condition’s increased flexibility for departure sequencing. However, it could also be thought that this would increase the problem’s solution space; indeed, increased flexibility can actually have a negative effect upon the problem difficulty, since it gives the person less guidance about whether their decision is correct or not. In the interval-based objective, participants had to make choices related to routing and scheduling, while the order-based condition reduced some of the need for planning as a stricter sequence was requested of participants. This increased complexity within the interval-based objective appeared to be the case here, since only one participant completed the interval-based game optimally.

Previous research in optimization problem solving with TSPs and CVRPs has identified an inverse effect between the number of nodes within the problem space and task performance (Kefalidou 2017; MacGregor et al. 1999). In the current study, the network layout did not produce a statistically significant effect on the likelihood of a participant solving the routing problem within the optimal number of turns and with the least delay. While this at first appears to challenge the established relationship between problem complexity (as measured by number of nodes) and task performance, we do not believe this is the case. We suggest that this actually reflects the aforementioned difference between network complexity and flexibility; although Board B was more complex in terms of node count, its physical configuration provided more opportunities for holding and/or reordering aircraft than Board A’s layout did. This has also been observed in an operational setting with professional runway controllers routing aircraft through the same holding areas that were used in the present study (Atkin 2008). This suggests that although Board B had a more nodes than Board A, the flexible configuration of Board B counteracted the effects of complexity.

Given this complexity, we hypothesize that a greater degree of planning and situation awareness would be needed to succeed in the interval-based condition. Although task complexity differed between the two objectives, this effect was only observed in the performance measures rather than in the perceptions of mental workload. While further work is needed to investigate this hypothesis, the findings suggest that aiding participants with route and schedule planning tasks may improve the odds of higher level performance.

6.1 Limitations

The findings of the current study are limited in several regards. First, the number of replications was minimal, leading to a relatively small sample. Second, the results do not necessarily reflect the behavior of expert ground movement controllers; nevertheless, the study was intended to focus on novice problem solvers and aimed to identify performance levels and heuristics used by non-experts. Third, the natures of the two objective conditions make it difficult to objectively compare performance between the two conditions. Fourth, some participants’ performances were affected by rule violations during the gameplay, but these were addressed by either removing affected records from analysis or correcting the errors during the game.

6.2 Implications and recommendations

Understanding patterns of behavior and performance in optimization problem solving provides insight into decision making which can aid the development of decision support algorithms, particularly in joint-cognitive systems where maintaining the human-in-the-loop is critical (Kefalidou 2017; Kefalidou and Ormerod 2014). This work has several implications relevant to the development of tower control DSS. First, the logistic regression analysis findings suggest that supporting tower controllers with planning activities (i.e., providing a target takeoff sequence to achieve rather than asking them to sequence within constraints) may improve their performance in routing and scheduling tasks. This is also supported by the analysis of strategies, in which participants who produced optimal solutions demonstrated a greater degree of projection and planning behavior. Further research is needed in order to explore processes involved in and factors affecting projection and planning. While the current study’s two objective conditions provided varying levels of sequencing support, the study did not provide routing support. Exploration of the effects of sequencing and routing guidance on solution optimality and task duration would be of value in the development of future tower control DSS. Furthermore, while the objective condition was not found to significantly affect mental workload, further research is needed to determine the degree to which planning support affects situation awareness in tower control tasks.

Secondly, while participants tended to switch strategies, construction of aircraft queues was frequently practiced, and successful routing strategies used the network layout to ensure flexibility (e.g., leaving the shortest path to the runway open in case of a delayed arrival). Sequential and near-sequential queuing appeared to shift cognitive demand from the participant and into the task environment. Constructing near-sequentially ordered queues allowed participants to manage the aggregated queue instead of needing to monitor individual cards constantly; a sequenced queue offers the benefit of a participant needing to consider the items at the front of a queue, a type of behavior that leverages the strengths of global information processing. It is possible that this type of global processing heuristic influenced participants’ levels of situation awareness, a factor that could be leveraged to support task performance in tower control.

Lastly, this research supports a human-centered approach to the design of DSS. We recommend exploring human behavior during optimization problem solving, both because of the potential to improve the body of knowledge related to human problem-solving theory, and also because developing an understanding of these processes can help to match the system’s guidance to user expectations. When systems lack reliability and transparency, their acceptance can be threatened (Beard et al. 2013). Moving toward a joint-cognitive systems approach for tower control DSS addresses this risk by considering the characteristics of human and technical agents and the interaction among them.

7 Conclusion

The study expands upon previous research showing that humans are capable of identifying optimal solutions in relatively short amounts of time (MacGregor and Ormerod 1996; Ormerod and Chronicle 1999). Whereas previous investigations into human optimization problem-solving behavior have primarily focused on variations on the traveling salesman problem and other vehicle routing problems, this work explored problem solving in the context of aircraft scheduling and routing in an airport tower control task, using novices in order to identify a baseline for strategic thinking and problem solving. The current work contributes to an enhanced understanding of how human decision makers engage in dynamic combinatorial optimization problem solving with the objective of informing future development of tower control DSS.