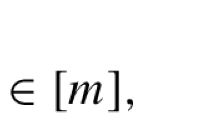Abstract
A nonconvex quadratically constrained quadratic programming (QCQP) with one constraint is usually solved via a dual SDP problem, or Moré’s algorithm based on iteratively solving linear systems. In this work we introduce an algorithm for QCQP that requires finding just one eigenpair of a generalized eigenvalue problem, and involves no outer iterations other than the (usually black-box) iterations for computing the eigenpair. Numerical experiments illustrate the efficiency and accuracy of our algorithm. We also analyze the QCQP solution extensively, including difficult cases, and show that the canonical form of a matrix pair gives a complete classification of the QCQP in terms of boundedness and attainability, and explain how to obtain a global solution whenever it exists.
Similar content being viewed by others
1 Introduction
A quadratically constrained quadratic programming (QCQP) is an optimization problem of the form [4, Sec. 4.4]
where A and \(B_i\) are \(n\times n\) symmetric matrices and \(a,b_i\in {\mathbb {R}}^n,\beta _i\in {\mathbb {R}}\). When A and \(B_i\) are all positive semidefinite, QCQP (1) is a convex problem, for which efficient algorithms are available such as the interior-point method [4, Ch. 11]. By contrast, when convexity is not assumed, QCQP is generally a difficult problem, in fact NP-hard in general [32]. Even when the constraints are all affine, i.e., \(B_i=0\), the decision problem formulation is known to be NP-complete [40]. All these are evidence that nonconvex QCQP is generally computationally intractable.
One exception to this difficulty is when \(k=1\), that is, when there is just one constraint:
This class of problems, namely QCQP with one quadratic constraint, includes the trust-region subproblem (TRS) as a special case [5, 26, Ch. 4], in which B is positive definite, \(b=0\) and \(\beta <0\). TRS is commonly employed for nonlinear optimization, and a number of efficient algorithms for solving TRS are available, e.g. [13, 25, 29, 31]. The QCQP (2) is sometimes called the generalized TRS [24], and has applications in double well potential problems [9] and compressed sensing for geological data, in which A is positive semidefinite and B is indefinite [18]. In this paper we refer to QCQP with one quadratic constraint (2) simply as QCQP, unless otherwise mentioned.
A dual formulation for QCQP (2) can be written as an semidefinite programming (SDP)
where \(X\succeq Y\) means \(X-Y\) is positive semidefinite. Remarkably, assuming Slater’s condition is satisfied, the SDP (3) is a dual problem with no duality gap, that is, the solution \(\gamma \) to (3) is equal to the optimal value of the QCQP (2), even when (2) is nonconvex; see [4, App. B] for details and a proof, which relies on the S-lemma [27]. The solution x can be obtained via the dual variable \(X=xx^{\top }\) of (3) in the non-hard case (otherwise \(\text{ rank }(X)\) is higher [29]). Nonconvex QCQP with one constraint (2) is thus a notable class of nonconvex optimization problems that can be solved in polynomial time. However, this SDP approach is not very efficient as solving the SDP (3) by the standard interior-point method involves an iterative process, each iteration requiring \(O(n^{3})\) operations [4, § 11.8.3] with a rather large constant, which limits the practical matrix size to, say, \(n\le 1000\).
Alternative strategies have been proposed in the literature. Moré [24] analyzes QCQP (2) and describes an algorithm that extends the algorithm of [25] for TRS. This algorithm is of an iterative nature, and is not matrix-free (a property desirable for dealing with large-sparse problems). Many other iterative algorithms have been proposed for TRS, but as indicated in the experiments in [1] for TRS, a one-step algorithm based on eigenvalues can significantly outperform such algorithms. Another approach [9, 16] is to note the Lagrange dual problem can be expressed equivalently as
This is a concave maximization problem, hence can be solved by e.g. a gradient descent method or Newton’s method. However, computing the gradient already involves \(O(n^3)\) operations, let alone the Hessian, and typically a rather large number of iterations is needed for convergence.
The main contribution of this paper is the development of an efficient algorithm for QCQP (2) that is strictly feasible and (A, B) is a definite pair with \(A+\lambda B\succ 0\) for some \(\lambda \ge 0\) (which we call definite feasible), which we argue is a generic condition for QCQP to be bounded.Footnote 1 The running time is \(O(n^3)\) when the matrices A, B are dense, and it can be significantly faster if the matrices are sparse. The algorithm requires (i) finding a \(\hat{\lambda }\ge 0\) such that \(A+\hat{\lambda }B\) is positive definite, and (ii) computing an extremal eigenpair of an \((2n+1)\times (2n+1)\) generalized eigenvalue problem. We emphasize that the algorithm requires just one eigenvalue problem. The algorithm is easy to implement given a routine for computing an extremal (largest or smallest) eigenpair, for which high-quality software based on shift-invert Arnoldi is publically available such as ARPACK [2, 22]. We present experiments that illustrate the efficiency and accuracy of our algorithm compared with the SDP-based approach. Our algorithm is based on the framework established in [1, 11, 17] of formulating the KKT conditions as an eigenvalue problem.
In addition, this paper also contributes to the theoretical understanding of QCQP, treating those that are not definite feasible. Specifically, it is a nontrivial problem to decide whether a given QCQP is bounded or not, and if bounded, whether the infimum is attainable. We present a classification of QCQP in terms of feasibility/boundedness/attainability, based on the canonical form of the symmetric pair (A, B) under congruence. We shall see that the canonical form provides rich information on the properties of the associated QCQP. We thus establish a process that (in exact arithmetic) solves QCQP completely in the sense that feasibility/boundedness/attainability is checked and the optimal objective value and a global solution is computed if it exists.
Broadly speaking, this paper is a contribution in the direction of “global optimization via eigenvalues”. To our knowledge the earliest reference is Gander, Golub and von Matt [11] for TRS. This algorithm was revisited and further developed recently in [1] to illustrate its high efficiency, which was extended in [34] to deal with an additional linear constraint. This paper is largely an outgrowth of [1], extending the scope from TRS to QCQP, relaxing the convexity assumption in the constraint, and fully analyzing the degenerate cases. We also note [33], which solves QCQP with an additional ball constraint (generalized CDT problem; GCDT) via a two-parameter eigenvalue problem. It is in principle possible to impose a ball constraint with sufficiently large radius to convert QCQP (2) to GCDT, then use the algorithm in [33]. However, this would be very inefficient, requiring \(O(n^6)\) operations: our algorithm here needs at most \(O(n^3)\) operations, and can be faster when sparsity structure is present.
This paper is organized as follows. In Sect. 2 we review (mostly existing) results on the optimality and boundedness of QCQP (2). Section. 3 is the heart of this paper where we derive our eigenvalue-based algorithm for definite feasible QCQP. We present numerical experiments in Sect. 4, and analyze QCQP that are not definite feasible in Sect. 5.
Notation. We denote by \({\mathcal {R}}(X)\) the range of a matrix X, and by \({\mathcal {N}}(X)\) the null space. \(X\succ (\succeq ) 0\) indicates X is a positive (semi)definite matrix. \(I_n\) is the \(n\times n\) identity, and \(O_n,O_{m\times n}\) are zero matrices of size \(n\times n\) and \(m\times n\). We simply write I, O if the dimensions are clear from the context. The Moore-Penrose pseudoinverse of a matrix A is denoted by \(A^\dagger \). \(x_*\) denotes a QCQP solution with associated Lagrange multiplier \(\lambda _*\).
2 Preliminaries: optimality and boundedness of QCQP
This section collects results on QCQP that are needed for our analysis and algorithm.
2.1 QCQP with no interior feasible point
QCQP (2) has no strictly feasible point when Slater’s condition is violated. Note that checking strict feasibility can be done by an unconstrained quadratic minimization problem \({{\mathrm{minimize}}}_x g(x)\). This subsection focuses on the case \(\min _x g(x)=0\).
Since \(\min _x g(x)>-\infty \), the quadratic function g(x) must be convex. Since further \(\min _x g(x)=0,\) we can write g(x) for some \(x'\in {\mathbb {R}}^n\) as
Now let \({\mathcal {N}}(B)\) be spanned by \(N=[\nu _1,\ldots ,\nu _j]\in {\mathbb {R}}^{n\times j}\). We can write \(g(x)=0\Leftrightarrow x=x'+Ny \) for some \(y\in {\mathbb {R}}^j\). Therefore the original QCQP is equivalent to the unconstrained problem
Thus, dealing with QCQP that violates Slater’s condition is straightforward. In what follows we treat strictly feasible QCQP for which there exist x with \(g(x)<0\) (i.e., Slater’s condition is satisfied).
2.2 Boundedness and attainability
We start with a necessary and sufficient condition for boundedness of a strictly feasible QCQP.
Lemma 1
(Hsia et al. [16], Thm. 5) Suppose that for QCQP (2), there exists an interior feasible point \(x\in {\mathbb {R}}^n\) such that \(g(x)<0\). Then f(x) is bounded below in the feasible region if and only if there exists \(\lambda \ge 0\) such that
Proof
This is essentially a corollary of strong duality between QCQP (2) and SDP (3), which is bounded below if and only if there exist \(\lambda \ge 0\) and \(\gamma \) satisfying the first constraint in (3), which is equivalent to (5). \(\square \)
Boundedness guarantees the existence of the optimal (infimum) value for f. On the other hand, it is worth noting that there exist QCQP that are bounded but has no solution \(x_*\). For example, consider
For any (x, y), we have \(x^2\ge 0\), and by taking \((x,y)=(\varepsilon ,1/\varepsilon )\) and \(\varepsilon \rightarrow 0\) the constraints are satisfied and the objective function approaches the infimum 0. However, no feasible (x, y) has the objective value equal to 0. Such QCQP, that is, QCQP for which the infimum cannot be attained in the feasible region, are called unattainable. A necessary and sufficient condition for unattainability is given in the following result (recall that \(\dagger \) denotes the pseudoinverse).
Lemma 2
(Hsia et al. [16], Thm. 7) Suppose that QCQP (2) is bounded and satisfies Slater’s condition. Then the QCQP is unattainable if and only if the set \(\{\lambda \ge 0|A+\lambda B\succeq 0\}\) is a single point \(\lambda _*\ge 0\), and the following has no solution in \(y\in {\mathcal {N}}(A+\lambda _* B)\):
A reasonable output of a numerical algorithm for such QCQP is the infimum objective value 0 with the warning that it is unattainable.
2.3 Optimality conditions
When QCQP (2) satisfies Slater’s condition and has a global solution, a set of necessary and sufficient conditions is given by Moré [24]:
Theorem 1
(Moré [24]) Suppose that QCQP (2) satisfies Slater’s condition. Then \(x_*\) is its global solution if and only if there exist \(\lambda _*\ge 0\) such that
The first three conditions in (8) represent the KKT conditions, and there can be many KKT points \((\lambda ,x)\) satisfying these three, reflecting the nonconvexity of the problem. The final condition \(A+\lambda _* B\succeq 0\) specifies which of the KKT points is the solution.
2.4 Definite feasible QCQP: strictly feasible and definite
By Lemma 1, for a strictly feasible QCQP to be bounded we necessarily need \(A+\hat{\lambda }B\succeq 0\) for some \(\hat{\lambda }\ge 0\). If we further have \(A+\hat{\lambda }B\succ 0\), then the QCQP is clearly bounded. As we argue in Sect. 5, such cases form a “generic” class of QCQP (2) that are bounded and has a global solution. We therefore give a name for such QCQP.
Definition 1
A QCQP (2) satisfying the following two conditions is said to be definite feasible.
-
1.
It is strictly feasible: there exists \(x\in {\mathbb {R}}^n\) such that \(g(x)<0\), and
-
2.
(A, B) is definite with nonnegative shift: there exists \(\hat{\lambda }\ge 0\) such that \(A+\hat{\lambda }B\succ 0\).
We shall treat such QCQP in detail and derive an efficient algorithm in Sect. 3. To begin with, for definite feasible QCQP there always exists a global solution \(x_*\).
Theorem 2
(Moré [24]) For a definite feasible QCQP (2), there exist \(x_*\in {\mathbb {R}}^n\), \(\lambda _*\ge 0\) such that the conditions (8) hold.
In the special case of TRS we have \(B\succ 0\), so by taking \(\hat{\lambda }\) arbitrarily large we have \(A+\hat{\lambda }B\succ 0\), and since Slater’s condition is trivially satisifed, it follows that TRS is a definite feasible QCQP. Similarly, if \(A\succ 0\), taking \(\hat{\lambda }=0\) shows the pencil is definite, so such QCQP is definite feasible as long as it is strictly feasible. Indeed a number of studies focus on such cases [8, 9].
2.4.1 Checking definite feasibility
Let us now discuss how to determine whether a given QCQP (2) is definite feasible.
Generally the values of \(\lambda \) for which \(A+\lambda B\succ 0\), if nonempty, is an open interval \(\tilde{D}=(\tilde{\lambda }_1,\tilde{\lambda }_2)\), allowing \(\tilde{\lambda }_1=-\infty \) and \(\tilde{\lambda }_2=\infty \), and the set of \(\lambda \) for which \(A+\lambda B\succeq 0\) is its closure [24] if \(\tilde{D}\) is nonempty. \(\tilde{\lambda }_1,\tilde{\lambda }_2\) are eigenvalues of the pencil \(A+\lambda B\) unless they are \(\pm \infty \).
In general, given a matrix pair (A, B), it is an active research area to devise algorithms for checking its definiteness (dropping the requirement \(\hat{\lambda }\ge 0\)), that is, checking whether there exist \(t\in {\mathbb {R}}\) such that \(A\sin t+B\cos t\succ 0\). Such algorithms include [6, 15], which also provide a value \(t_0\) for which \(A\sin t_0+B\cos t_0\succ 0\) if (A, B) is definite. If the pair (A, B) is determined not to be definite then QCQP is not definite feasible. If the pair (A, B) is determined to be definite, with \(t_0\) available such that \(A\sin t_0+B\cos t_0\succ 0\), then we compute the smallest eigenvalue \(\lambda _1\) and largest eigenvalue \(\lambda _2\) of the pencil
Then the matrix \((A\cos t_0-B\sin t_0)+\lambda (A\sin t_0+B\cos t_0)\) is positive semidefinite for \(\lambda \ge \lambda _2\), and negative semidefinite for \(\lambda \le \lambda _1\). Hence we can rewrite the condition \(A\sin t+B\cos t\succ 0 ~ (|t-t_0|<\pi )\) as
thus we obtain the interval \(t\in (t_1,t_2)\) on which \(A\sin t+B\cos t\succ 0\). From this we obtain the interval \(\tilde{D}=\{\frac{1}{\tan t} \mid t\in (t_1,t_2), \sin t>0, \cos t\ge 0\}\) such that \(A+\lambda B\succ 0\) if and only if \(\lambda \in \tilde{D}\). If \(D=\tilde{D}\cap [0,\infty )\) is empty then the QCQP is not definite feasible; otherwise it is.
3 Eigenvalue-based algorithm for definite feasible QCQP
We now develop an eigenvalue algorithm for definite feasible QCQP. In this section we assume that a value of \(\hat{\lambda }\ge 0\) such that \(A+\hat{\lambda }B\succ 0\) is known, through a process such as those described in Sect. 2.4.1.
By Theorems 1 and 2, a definite feasible QCQP can be solved by solving (8) for \(\lambda _*\) and \(x_*\). We develop an algorithm that first finds the optimal Lagrange multiplier \(\lambda _*\) by an eigenvalue problem, then computes \(x_*\).
3.1 Preparations
First, let \(D\) be the interval \(\{\lambda \ge 0|A+\lambda B\succ 0\}\). We denote the left-end of \(D\) by \(\lambda _1\), and the right-end by \(\lambda _2\). Note that \(\lambda _2=\tilde{\lambda }_2\), but due to the requirement \(\lambda \ge 0\), the left-end of \(D\) may not be the same as \(\tilde{\lambda }_1\) in Sect. 2.4.1. We have either \(D=(\lambda _1,\lambda _2)\) if \(\lambda _1>0\), or \(D=[\lambda _1,\lambda _2)\), which happens if \(A\succ 0\) and hence \(\lambda _1=0\).
For \(\lambda \in D\), define
In view of the third condition in (8), the main goal is to find \(\lambda _*\) such that \(\gamma (\lambda _*)=0\). This argument apparently dismisses the cases where \(A+\lambda _* B\) is singular (then \(x(\lambda )\) is not well-defined) or \(\lambda _*=0\) (then \(\gamma (\lambda )=0\) is unnecessary). Nonetheless, the analysis below will cover such cases.
Since \(A+\hat{\lambda }B\succ 0\), A and B are simultaneously diagonalizable, that is, there exists a nonsingular \(W\in {\mathbb {R}}^{n\times n}\) such that \(W^\top AW\) and \(W^\top BW\) are both diagonal [12, Chap. 8]. Hence without loss of generality we assume that A, B are diagonal in the analysis below (our algorithm does not assume this or the knowledge of W). Let \(A=\mathrm{diag}(d_1,\ldots ,d_n)\), \(B=\mathrm{diag}(e_1,\ldots ,e_n)\), \(a=[a_1,\ldots ,a_n]^\top \), and \(b=[b_1,\ldots ,b_n]^\top \) (those a and b are indeed \(W^\top a\) and \(W^\top b\) in the original coordinate system). It is now straightforward to identify the interval \(D\). Since
when \(0<\lambda _1<\lambda _2<\infty \) there exist \(i_1\) and \(i_2\) so that \(d_{i_1}+\lambda _1e_{i_1}=0\) and \(d_{i_2}+\lambda _2e_{i_2}=0\).
\(\gamma (\lambda )\) can be explicitly expressed using \(x(\lambda )=[x_1(\lambda ),\ldots ,x_n(\lambda )]^\top \) as
Therefore \(x_i(\lambda )\) and \(\gamma (\lambda )\) are rational functions of \(\lambda \). Moreover, on \(\lambda \in D\), the function \(\gamma (\lambda )\) has the following property [24, Thm. 5.2].
Proposition 1
(Moré [24]) \(\gamma (\lambda )\) is monotonically nonincreasing on \(\lambda \in \tilde{D}=(\tilde{\lambda }_1,\tilde{\lambda }_2)\supseteq D\). Moreover, excluding the case where \(x(\lambda )\) is a constant, \(\gamma (\lambda )\) is monotonically strictly decreasing on \(\lambda \in \tilde{D}\).
3.2 Classification of definite feasible QCQP
In order to investigate the properties of \(\lambda _*\) that satisfy (8), in particular \(\gamma (\lambda _*)=0\), we separate definite feasible QCQP (2) into four distinct cases, depending on the sign of \(\gamma (\lambda )\) on \(\lambda \in D\).
-
(a)
\(\gamma (\lambda )\) takes both nonnegative and nonpositive values.
-
(b)
\(\gamma (\lambda )>0\) everywhere.
-
(c)
\(\gamma (\lambda )<0\) everywhere, and \(\lambda _1>0\).
-
(d)
\(\gamma (\lambda )<0\) everywhere, and \(\lambda _1=0\).
We now investigate the value of \(\lambda _*\) for each case.
First for (a), by the mean-value theorem there exists \(\lambda \in D\) such that \(\gamma (\lambda )=0\), and for this \(\lambda \) we have \(\lambda _*=\lambda \).
To deal with cases (b), (c) we use the following result.
Proposition 2
The following results hold for definite feasible QCQP (2) for which \(A+\lambda B\succ 0\) on \(\lambda \in D\).
-
1.
Suppose case (b) holds with \(\lambda _2<\infty \). Then \(x(\lambda )\) converges as \(\lambda \nearrow \lambda _2\) and there exists x with \(g(x)=0,(A+\lambda _2 B)x=-(a+\lambda _2 b)\).
-
2.
Suppose case (c) holds with \(\lambda _1>0\). Then \(x(\lambda )\) converges as \(\lambda \searrow \lambda _1\), and there exists x with \(g(x)=0\) and \((A+\lambda _1 B)x=-(a+\lambda _1 b)\).
Proof
Suppose case (b) holds with \(\lambda _2<\infty \). Since \(\lambda _2=-\frac{d_{i_2}}{e_{i_2}}<\infty \) we have \(e_{i_2}\ne 0\) and further \(e_{i_2}<0\) from (10), which holds even if \(i_2\) contains multiple elements. Note also that \(x(\lambda _2)_i\) are bounded constants for all \(i\notin i_2\). Hence by (12), \(\gamma (\lambda )\) is a quadratic equation in \(x(\lambda )_{i_2}\) with negative leading coefficient, and so for the assumption \(\gamma (\lambda _2)>0\) to hold, \(|x(\lambda _2)_{i_2}|\) cannot blow up to \(\infty \). Hence by (11) we must have \(a_{i_2}+\lambda _{2} b_{i_2}=0\), and thus \(x(\lambda _2)\) converges to the vector (11) with the \(i_2\)th element \(x(\lambda _2)_{i_2} = -\frac{b_{i_2}}{e_{i_2}}\). Now, any vector x equal to \(x(\lambda _2)\) with the \(i_2\)th element replaced with an arbitrary number satisfies \((A+\lambda _2 B)x=-(a+\lambda _2 b)\); we shall choose this \(i_2\)th element of x—which we denote by y —so that \(g(x_y)=0\), where we made the y-dependence of x explicit. Then \(g(x_y)=0\) is a quadratic equation in y with negative leading coefficient \(e_{i_2}\). Together with the assumption \(g(x_{-b_{i_2}/e_{i_2}})>0\), there are two real solutions in y to \(g(x_y)=0\). With either root, the vector \(x:=x_y\) satisfies \(g(x)=0,(A+\lambda _2 B)x=-(a+\lambda _2 b)\).
The the case (c) with \(\lambda _1>0\) is similar: We need \(a_{i_1}+\lambda _{1} b_{i_1}=0\), and \(x(\lambda _1)\) converges to the vector (11) with the \(i_1\)th element \(x(\lambda _1)_{i_1} = -\frac{b_{i_1}}{e_{i_1}}\). Define the vector \(x_y\) to be equal to \(x(\lambda _1)\) except the \(i_1\)th element y, which is set so that \(g(x_y)=0\). Then \(x:=x_y\) satisfies the two equations. \(\square \)
We note that it is possible to prove Proposition 2 as a straightforward corollary of [9, Lemma 2].
By Proposition 2, in case (b) we have \(\lambda _*=\lambda _2\) when \(\lambda _2<\infty \). Similarly, in case (c) we have \(\lambda _*=\lambda _1\). In Proposition 2 we assumed \(\lambda _2<\infty \), but indeed Slater’s condition assures that \(\lambda _2=\infty \) and \(\gamma (\lambda _2)>0\) cannot happen.
Proposition 3
Suppose that \(\lambda _2=\infty \) for a definite feasible QCQP. Then \(\lim _{\lambda \rightarrow \infty }\gamma (\lambda )<0\).
Proof
Suppose to the contrary that \(\lim _{\lambda \rightarrow \infty }\gamma (\lambda )\ge 0\). \(\gamma (\lambda )\ge 0\) as \(\lambda \rightarrow \infty \). Then since \(\gamma (\lambda )\) is nonincreasing on \((\lambda _1,\infty )\), we see that \(\gamma (\lambda )\) converges, and let \(\gamma _\infty \) be the limit. Now if we suppose that \(x_i(\lambda )\) diverges, then by (11) we have \(e_i=0,d_i>0\) and \(b_i\ne 0\). Hence as \(\lambda \rightarrow \infty \) we have
which, by (12), indicates \(\gamma (\lambda )\rightarrow -\infty \), a contradiction. Thus \(x(\lambda )\) converges, and let \(\bar{x}\) be the limit. Then we have \(B\bar{x}=-b\), so
By the assumption \(\lambda _2=\infty \), taking \(\lambda \rightarrow \infty \) we have \(A+\lambda B\succeq 0\), so \(B\succeq 0\). Thus for any \(x\in {\mathbb {R}}^n\) we have
must always hold, which contradicts the fact that there exists x such that \(g(x)<0\). \(\square \)
An alternative way to understand Proposition 3 is to note that \(\lambda _2=\infty \), including \(B\succ 0\), indicates the QCQP (2) is essentially a TRS (after an affine change-of-variables), for which a solution for \(\gamma (\lambda _*)=0\) is known to exist [1]. One can actually show \(\lim _{\lambda \rightarrow \infty }\gamma (\lambda )=\min _xg(x)\) (which is \(<0\) by assumption), based on [28, Lemma 2.3].
Finally, consider case (d). Since \(\gamma (\lambda )\le 0\) as \(\lambda \rightarrow +0\), letting \(x_0\) be the limit (which exists [9]) we have \(g(x_0)\le 0\) and \(Ax_0=-a\), so taking \(\lambda _*=0\), \(x_*=x_0\) we see that the conditions (8) are satisfied.
Summarizing, the values of \(\lambda _*\) in Theorem 2 are
Figures 1, 2, 3 and 4 illustrate typical plots of \(\gamma (\lambda )\) for the four cases.
3.3 Computing the Lagrange multiplier \(\lambda _*\)
We now consider computing \(\lambda _*>0\) that satisfies (8). The material in this subsection is the key ingredient of the algorithm that we propose. We need to find \(\lambda _*, x_*\) such that
In principle, this can be done by solving \(\gamma (\lambda )=0\) for \(\lambda \), which is a rational equation. However, when A, B are not diagonal (as is usually the case), expressing \(\gamma (\lambda )\) explicitly in rational function form is a nontrivial task.
Our approach, building upon [1, 11] for the TRS, is to express \(\gamma (\lambda )=0\) as a generalized eigenvalue problem.
Define \(M_0,M_1\in {\mathbb {R}}^{(2n+1)\times (2n+1)}\) as
Then we show that the the optimal Lagrange multiplier \(\lambda _*>0\) in (8) is an eigenvalue of \(M_0+\lambda M_1\), that is, there exists a nonzero vector \(z\in {\mathbb {R}}^{2n+1}\) such that
Theorem 3
\(\det (M_0+\lambda M_1)\) has the expression
and for \(\lambda _*>0\) satisfying (8), \(\lambda =\lambda _*\) satisfies
Proof
For \(\lambda \) for which \(\det (A+\lambda B)\ne 0\), we have
Hence if \(A+\lambda _* B\) is nonsingular, then (18) holds with \(\gamma (\lambda _*)=0\), and hence we have \(\det (M_0+\lambda _* M_1)=0\).
When \(A+\lambda _* B\) is singular, we have \(a+\lambda _* b=-(A+\lambda _*B)x_*\in {\mathcal {R}}(A+\lambda _* B)\), hence the bottom n rows of \(M_0+\lambda _* M_1\) have rank \((n-1)\) or less, hence \(\det (M_0+\lambda _* M_1)=0\). \(\square \)
The above proof also shows that any KKT multiplier \(\lambda \) satisfying the first three equations in (8) is an eigenvalue of \(M_0+\lambda M_1\). Note from (18) and the fact \(A+\hat{\lambda }B\succ 0\) that we either have \(\det (M_0+\hat{\lambda }M_1)\ne 0\), indicating \(M_0+\lambda M_1\) is a regular matrix pencil (thus having exactly \(2n+1\) eigenvalues), or that \(\det (M_0+\hat{\lambda }M_1)= 0\), in which case \((\hat{\lambda },x(\hat{\lambda }))\) satisfies all the conditions in (8), thus is a solution for QCQP (2). It thus follows that \(\lambda _*\) can be found (or at least a finite set containing it) via the eigenvalue problem \(\det (M_0+\lambda M_1)= 0\). Note from Proposition 1 that \(M_0+\lambda M_1\) is regular unless \(\gamma (\lambda )\) is identically zero, in which case every value of \(\lambda \) for which \(A+\lambda B\succ 0\) is an optimal Lagrange multiplier. Since this case is easy, in what follows we assume \(M_0+\lambda M_1\) is regular.
We shall further show that \(\lambda _*\) is the unique eigenvalue of \(M_0+\lambda M_1\) in the interval \(D=(\lambda _1,\lambda _2)\). To simplify the analysis, we apply a Möbius transformation [23] to the matrix pencil (15). Specifically, recalling that \(\hat{\lambda }\ge 0\) is known such that \(A+\hat{\lambda }B\succ 0\), we define \(\hat{M}:=M_0+\hat{\lambda }M_1\) and consider the eigenvalues of
The eigenvalues \(\xi \) of (19) correspond one-to-one to those \(\lambda \) of \(M_0+\lambda M_1\) via the transformation \(\lambda =\hat{\lambda }+\xi ^{-1}\). We consider only \(\xi \ne 0\), as \(\xi =0\) corresponds to the eigenvalue of \(M_0+\lambda M_1\) at infinity, which is irrelevant. We shall show that the largest (or smallest) real eigenvalue \(\xi _*\) of (19) gives the value \(\lambda _*=\hat{\lambda }+\xi ^{-1}_*\) in (8).
We consider separate cases depending on the sign of \(\gamma (\hat{\lambda })\), and we next show that in both cases it suffices to compute one extremal eigenpair of (19).
Lemma 3
-
1.
When \(\gamma (\hat{\lambda })>0\), the smallest real eigenvalue \(\lambda =\lambda _*\) of (15) larger than \(\hat{\lambda }\) satisfies \(\hat{\lambda }<\lambda _*\le \lambda _2\).
-
2.
Similarly, when \(\gamma (\hat{\lambda })<0\), the largest real eigenvalue \(\lambda =\lambda _*\) of (15) smaller than \(\hat{\lambda }\) satisfies \(\lambda _1\le \lambda _*<\hat{\lambda }\), except in case (d).
-
3.
When \(\gamma (\hat{\lambda })<0\) and case (d) happens, the largest real eigenvalue \(\lambda =\lambda _*\) of (15) smaller than \(\hat{\lambda }\) satisfies \(\lambda _*\le \lambda _1=0\), or there is no \(\lambda _*<\hat{\lambda }\) satisfying \(\gamma (\lambda _*)=0.\)
Proof
Except in case (d), \(\gamma (\lambda )\) is monotically strictly decreasing on \(\lambda \in \tilde{D}\) by Proposition (1). In this case, by (13) and Theorem 3, \(\lambda =\lambda _*>0\) satisfies (17). Checking (13) and the sign of \(\gamma (\hat{\lambda })\), we complete the proof for all cases but (d).
In case (d), there is no nonnegative \(\lambda <\lambda _2\) that satisfies \(\gamma (\lambda )=0\). Two possibilities are (i) \(\lambda _*\le 0\) exists such that \(\gamma (\lambda _*)=0\), or (ii) no such \(\lambda _*\) exists. This completes the proof.
We note that in Lemma 3, eigenvalues \(\lambda =\pm \infty \) of (15) are not allowed.
3.3.1 When \(\gamma (\hat{\lambda })=0\)
In this case \(\gamma (\hat{\lambda })=g(x(\hat{\lambda }))=0\), so \((\lambda _*,x_*)=(\hat{\lambda },x(\hat{\lambda }))\) satisfies (8). Hence in this case we are done; there is no need to solve the generalized eigenvalue problem.
3.3.2 When \(\gamma (\hat{\lambda })>0\)
Theorem 4
Suppose \(\gamma (\hat{\lambda })>0\). Then for the largest finite real eigenvalue \(\xi '\) of (19) it holds \(\xi '>0\), and the optimal Lagrange multiplier satisfying (8) is \(\lambda _*=\hat{\lambda }+\xi '^{-1}\).
Proof
Using the same \(\lambda _*\) as in Lemma 3, \(\xi _*=(\lambda _*-\hat{\lambda })^{-1}\) is an eigenvalue of (19). By Lemma 3, \(\xi '\ge \xi _*=(\lambda _*-\hat{\lambda })^{-1}>0.\)
If \(\xi '> \xi _*\), \(\lambda =\hat{\lambda }+\xi '^{-1}\) becomes the smallest real eigenvalue of (15) larger than \(\hat{\lambda }\), which contradicts Lemma 3. Therefore \(\xi '=\xi _*,\) and \(\lambda _*=\hat{\lambda }+\xi '^{-1}\). \(\square \)
Theorem 4 shows that when \(\gamma (\hat{\lambda })>0\), the optimal Lagrange multiplier \(\lambda _*\) can be obtained by computing the largest real eigenvalue of (19). One practical difficulty here is that by an algorithm such as shift-and-invert Arnoldi, it can be much harder to compute the largest real eigenvalue than the eigenvalue with largest real part (which can be complex). We shall now show that in fact these are the same for (19), that is, its rightmost eigenvalue is real. A similar statement was made in [1] for the special case of TRS; here we extend the result to definite feasible QCQP.
Theorem 5
Let \(\gamma (\hat{\lambda })>0\). Then the rightmost finite eigenvalue of the pencil (19) is real.
Proof
It suffices to prove that for every \(\xi =s+t{\text {i}}\) with \(s\ge \xi '\) and \(t\ne 0\), we have \(\det (M_1+\xi \hat{M})\ne 0\), or equivalently (by (18)), that \(\det (A+(\hat{\lambda }+\xi ^{-1})B)\ne 0\) and \(\gamma (\hat{\lambda }+\xi ^{-1})\ne 0\).
First consider values of \(\lambda \) such that \(\det (A+\lambda B)=0\). These are the eigenvalues \(\lambda =-\frac{d_i}{e_i}\) of \(A+\lambda B\). In particular, when \(\lambda \) is nonreal we have \(\det (A+\lambda B)\ne 0\), and so \(\det (A+(\hat{\lambda }+\xi ^{-1})B)\ne 0\).
We next examine the imaginary part of \(\gamma (\hat{\lambda }+\xi ^{-1})\). Defining \(\hat{\lambda }+\xi ^{-1}=p+q{\text {i}}\) we have
Now \(p=\hat{\lambda }+s(s^2+t^2)^{-1}\), and since \(0<\xi '\le s\) we obtain
hence \(p\in D\). In other words, \(d_k+pe_k>0 \ (k=1,\ldots ,n)\). By \(\gamma (\hat{\lambda })\ne 0\) and Proposition 1 we see that for some k we have \(b_kd_k-a_ke_k\ne 0\), so by \(q\ne 0\)
Hence \(\gamma (\hat{\lambda }+\xi ^{-1})\ne 0\), completing the proof. \(\square \)
The upshot is that to obtain the optimal Lagrange multiplier \(\lambda _*\) when \(\gamma (\hat{\lambda })>0\), it suffices to compute the rightmost eigenpair of (19).
3.3.3 When \(\gamma (\hat{\lambda })<0\)
This case can be treated in essentially the same way as above, but special treatment is necessary for the case (d).
Theorem 6
Suppose \(\gamma (\hat{\lambda })<0\). Let \(\xi '\) be the leftmost real finite eigenvalue of (19). If \(\hat{\lambda }=0\) or \(-\hat{\lambda }^{-1}\le \xi '\le 0\), the case corresponds to (d), and we have \(\lambda _*=0\). If \(\hat{\lambda }>0\) and \(\xi '<-\hat{\lambda }^{-1}\), then \(\lambda _*=\hat{\lambda }+\xi '^{-1}\).
Proof
If \(\hat{\lambda }=0\) then \(0\le \lambda _1\le \hat{\lambda }=0\), which happens only in case (d). If \(-\hat{\lambda }^{-1}\le \xi '\le 0\) then \(\hat{\lambda }+\xi '^{-1}\le 0\) or \(\xi '=0\) holds. These conditions imply that the largest eigenvalue of (15) smaller than \(\hat{\lambda }\) is nonpositive, or (15) has no nonpositive eigenvalue. By Lemma 3, these occur only in case (d).
Now suppose \(\hat{\lambda }>0\) and \(\xi '<-\hat{\lambda }^{-1}\). These conditions imply \(\hat{\lambda }+\xi '^{-1}>0\) and \(\det (M_0+(\hat{\lambda }+\xi '^{-1})M_1)=0\), therefore the case (d) does not occur. By \(\hat{\lambda }+\xi '^{-1}\le \hat{\lambda }\) and \(\det (M_0+(\hat{\lambda }+\xi '^{-1})M_1)=0\) we have \(\hat{\lambda }+\xi '^{-1}\le \lambda _*\). If \(\hat{\lambda }+\xi '^{-1}<\lambda _*\), \(\lambda =\hat{\lambda }+\xi '^{-1}\) becomes the largest real eigenvalue of (15) smaller than \(\hat{\lambda }\), which contradicts Lemma 3. Therefore \(\lambda _*=\hat{\lambda }+\xi '^{-1}\). \(\square \)
The following is an analogue of Theorem 5.
Theorem 7
Suppose that \(\gamma (\hat{\lambda })<0\), and that for the leftmost real finite eigenvalue \(\xi '\) of (19), \(\xi =s+t{\mathrm {i}}\) satisfies \(s\le \xi '\), \(t\ne 0\) and \(\xi \) is an eigenvalue of (19). Then this corresponds to case (d), and \(\text{ Re }(\hat{\lambda }+\xi ^{-1})\le 0\).
Proof
We first prove that cases (a) and (c) cannot satisfy the assumptions. Indeed by Theorem 6 we have \(\xi '<-\hat{\lambda }^{-1}<0\), so writing \(\hat{\lambda }+\xi ^{-1}=p+q{\text {i}}\) we have
Since \(\lambda ',\hat{\lambda }\in D\), we have \(\hat{\lambda }+s^{-1}\in D\). Then as in the proof of Theorem 5 we see that \(\xi \) is not a solution for (19), a contradiction.
Now suppose we are in case (d). Since \(D\) is bounded below by 0, if \(0<\lambda \le \hat{\lambda }\) then \(\lambda \in D\). Also, since \(p\le \hat{\lambda }\) always holds, if \(p>0\) then by \(0<p\le \hat{\lambda }\) we have \(p\in D\), so as in the proof of Theorem 5 we see that \(\xi \) is not a solution for (19), again a contradiction. Thus we conclude that \(p={\text {Re}}(\hat{\lambda }+\xi ^{-1})\le 0\).
In case (d) with \(\hat{\lambda }=0\), using the fact that \(\xi =0\) is always a solution of (19), we obtain \(\text{ Re }(\xi )\le \xi '\le 0\) and \(\text{ Re }(\hat{\lambda }+\xi ^{-1})=\text{ Re }(\xi ^{-1})\le 0\). \(\square \)
In summary, when \(\gamma (\hat{\lambda })<0\) we can obtain \(\lambda _*\) in (8) by computing the leftmost eigenvalue \(\xi _*\) of (19) and choosing \(\lambda _*\) depending on the value of \(\hat{\lambda }+\xi _*^{-1}\) as follows:
-
if \(\hat{\lambda }+\xi _*^{-1}>0\), take \(\lambda _*=\hat{\lambda }+\xi _*^{-1}\)
-
if either \(\hat{\lambda }=0\), \(\text{ Re }(\hat{\lambda }+\xi _*^{-1})\le 0\), or if \(\xi _*=0\), take \(\lambda _*=0\).
3.3.4 Pseudocode for computing \(\lambda _*\)
We summarize the whole process for finding \(\lambda _*\) in Algorithm 3.1.

As discussed before, we can compute the rightmost (or leftmost) eigenpair of a generalized eigenvalue problem using the Arnoldi method, which is much more efficient than computing all the eigenvalues, especially when the matrices have structure such as symmetry and/or sparsity. In Matlab the eigs command with the flag ’lr’ (’sr’) computes such eigenpair.
3.4 Obtaining the solution \(x_*\)
Having computed the optimal Lagrange multiplier \(\lambda _*\), we now turn to finding the solution \(x_*\). We shall show that generically the eigenvector z obtained in Algorithm 3.1 contains the desired information on \(x_*\).
First, if the output of Algorithm 3.1 is \(\lambda _*=0\), then the QCQP solution is simply \(-A^{-1}a\), the solution of a linear system (see Sect. 3.4.2 for the case \(\det (A)=0\)).
For nonzero \(\lambda _*\), we can generically obtain the solution by computing \(x_*=-(A+\lambda _* B)^{-1}(a+\lambda _* b)\), but below we show that solving such linear system is usually unnecessary.
3.4.1 When \(A+\lambda _* B\) is nonsingular
If \(\lambda _*>0\) and \(\det (A+\lambda _* B)\ne 0\), then we can obtain \(x_*\) via the eigenvector associated with \(\lambda _*\) (which is obtained by the Arnoldi method). Suppose \(z=[\theta \ y_1^\top \ y_2^\top ]^\top \) is the computed eigenvector where \(\theta \in {\mathbb {R}},y_1,y_2\in {\mathbb {R}}^n\).
Plugging \(z=[\theta \ y_1^\top \ y_2^\top ]^\top \) into \(M_0z+\lambda _* M_1z=0\) gives
First suppose \(\theta \ne 0\), which holds generically. Then from the last equation we see that the solution is \(x_*=\frac{y_1}{\theta }\).
Next suppose that \(\theta =0\). By (21), if \(y_1\ne 0\) then \(y_1\in {\mathcal {N}}(A+\lambda _* B)\), and \(A+\lambda _* B\) is singular. When \(y_1=0\), by (20) we have \(y_2\in {\mathcal {N}}(A+\lambda _* B)\) so again \(A+\lambda _* B\) is singular. Thus when \(A+\lambda _* B\) is nonsingular we necessarily have \(\theta \ne 0\), and thus we can obtain \(x_*\) directly from the eigenvector z.
3.4.2 When \(A+\lambda _* B\) is singular
When \(A+\lambda _* B\) is singular at the \(\lambda _*\) obtained by Algorithm 3.1, matters are more subtle. In this case we need to solve the linear system
which has a singular coefficient matrix \(A+\lambda _* B\). A singular linear system generically does not have a solution, but (8) shows that (22) must be consistent. However, the error of a computed solution to a linear system is generally proportional to the condition number, and solving a singular linear system numerically is challenging, if not impossible.
In fact, the case where \(A+\lambda _* B\) is singular corresponds to the well known “hard case” for the special case of TRS. For TRS, dealing with such hard cases are discussed in [25, 30]. In this work we discuss dealing with the hard case for the general QCQP by forming and solving a nonsingular linear system that has the same solution as (22). The development here parallels that in [1], which is in turn based on [10].
The following theorem will be the basis for the construction of \(x_*\).
Theorem 8
For \(\lambda _*\) satisfying (8), suppose \(A+\lambda _* B\) is singular. Let \(v_1,\ldots v_j\) be a basis for \({\mathcal {N}}(A+\lambda _* B)\), and let \(w_*\) be the solution of the linear system \(\tilde{A}w_*=-\tilde{a}\), where
in which \(\alpha >0\) is an arbitrary positive number. Then the following hold:
-
1.
\(\tilde{A}\succ 0\), in particular, \(\tilde{A}\) is nonsingular (hence \(w_*\) above exists uniquely),
-
2.
\((A+\lambda _* B)w_*=-(a+\lambda _* b)\),
-
3.
\((Bw_*+b)^\top v=0\) for every \(v\in {\mathcal {N}}(A+\lambda _* B)\).
To prove the theorem we prepare a lemma, which we will use repeatedly.
Lemma 4
For a definite feasible QCQP (2), if \(x\in {\mathcal {N}}(A+\lambda _* B)\) and \(x^\top Bx=0\) then \(x=0\).
Proof
We have
and \(A+\hat{\lambda }B\succ 0\), hence \(x=0\). \(\square \)
We are now ready to prove Theorem 8.
Proof
(for Theorem 8) We give a proof for each claim.
-
1.
By \(A+\lambda _* B\succeq 0\) and \(\sum _{i=1}^{j}Bv_iv_i^\top B\succeq 0\), we trivially have \(\tilde{A}\succeq 0\). For any \(x\in {\mathbb {R}}^n\), there exist a unique \(x_0\in {\mathcal {N}}(A+\lambda _* B)\) and \(x_1\in {\mathcal {R}}(A+\lambda _* B)\) such that \(x=x_0+x_1\). Let x be a vector such that \(x^\top \tilde{A}x=0\). We show that \(x=0\). We have \( x^\top \tilde{A}x=x_1^\top (A+\lambda _* B)x_1+\alpha \sum _{i=1}^{j}(v_i^\top Bx)^2=0, \) hence
$$\begin{aligned} x_1^\top (A+\lambda _* B)x_1=0,\quad \text{ and } \quad v_i^\top Bx=0\ (i=1,\ldots ,j) . \end{aligned}$$(24)Since \((A+\lambda _* B)\succeq 0\) we have \((A+\lambda _* B)x_1=0\), and hence \(x_1\in {\mathcal {N}}(A+\lambda _* B)\). Together with the assumption \(x_1\in {\mathcal {R}}(A+\lambda _* B)\) we obtain \(x_1=0\). Therefore, \(x=x_0\) can be written as \(x=\sum _{i=1}^{j}c_iv_i\), for some constants \(c_1,\ldots ,c_j\), so together with (24) we obtain \(x^\top Bx=\sum _{i=1}^{j}c_iv_i^\top Bx=0\). Combining this with \(x^\top (A+\lambda _* B)x=0\) and Lemma 4 we obtain \(x=0\). Therefore \(\tilde{A}\succ 0\).
-
2.
We shall first prove that
$$\begin{aligned} u_i:=\tilde{A}^{-1}Bv_i\in {\mathcal {N}}(A+\lambda _* B),\quad i=1,\ldots ,j. \end{aligned}$$(25)From \(\tilde{A}u_i=Bv_i,\) we have
$$\begin{aligned} (A+\lambda _* B)u_i&=Bv_i-\alpha \sum _{k=1}^{j}\left( v_k^\top Bu_i\right) Bv_k\\&=B\Big (v_i-\alpha \sum _{k=1}^{j}\left( v_k^\top Bu_i\right) v_k \Big ) =:Bv_i', \end{aligned}$$where we defined \(v'_i:=v_i-\alpha \sum _{k=1}^{j}(v_k^\top Bu_i)v_k\). Since \(v'_i\in {\mathcal {N}}(A+\lambda _* B)\) we have \((v'_i)^\top Bv'_i=(v'_i)^\top (A+\lambda _*B)u_i=0\). Therefore by Lemma 4 we have \(v'_i=0\), so \((A+\lambda _* B)u_i=0\), hence \(u_i\in {\mathcal {N}}(A+\lambda _* B)\), establishing (25). From this it follows that \((A+\lambda _* B)\tilde{A}^{-1}Bv_i=0\), and
$$\begin{aligned} (A+\lambda _* B)w_*+(a+\lambda _* b)&=-(A+\lambda _* B)\tilde{A}^{-1}\tilde{a}+(a+\lambda _* b) \\&=-(A+\lambda _* B)\tilde{A}^{-1}\left( a+\lambda _* b+\alpha \sum _{i=1}^{j}Bv_iv_i^\top b\right) \\&\qquad +(a+\lambda _* b)\\&=-(A+\lambda _* B-\tilde{A})\tilde{A}^{-1}(a+\lambda _* b)\\&\quad -\alpha \sum _{i=1}^{j}((A+\lambda _* B)\tilde{A}^{-1}Bv_i)v_i^\top b \\&=\alpha \sum _{i=1}^{j}Bv_i\left( v_i^\top B\tilde{A}^{-1}(a+\lambda _* b)\right) , \end{aligned}$$where for the last equality we used \((A+\lambda _* B)\tilde{A}^{-1}Bv_i=0\) and (23). Now from (8) we see that there exists \(x_*\) such that \(a+\lambda _* b=-(A+\lambda _* B)x_*\), so \(v_i^\top B\tilde{A}^{-1}(a+\lambda _* b)=-u_i^\top (A+\lambda _* B)x_*=0\) for \(i=1,\ldots ,j\), and \((A+\lambda _* B)w_*=-(a+\lambda _* b)\).
-
3.
For any \(v\in {\mathcal {N}}(A+\lambda _* B)\), we have
$$\begin{aligned} (Bw_*+b)^\top v&=(-B\tilde{A}^{-1}\tilde{a}+b)^\top v=\Big (-B\tilde{A}^{-1}\Big (a+\lambda _* b+\alpha \sum _{i=1}^{j}Bv_iv_i^\top b\Big )+b\Big )^\top v\nonumber \\&=-b^\top \Big (B\tilde{A}^{-1}\alpha \sum _{i=1}^{j}Bv_iv_i^\top \Big )^\top v+b^\top v\nonumber \\&=-b^\top \Big (\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}B\Big ) v+b^\top v =:-b^\top Lv+b^\top v, \end{aligned}$$(26)where we define \(L:=\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}B\). Next, suppose that \(Lx=0\) and \(x\in {\mathcal {N}}(A+\lambda _*B)\). We show that \(x=0.\) To this end, note that
$$\begin{aligned} Lx=\alpha \sum _{i=1}^{j}\left( v_i^\top B\tilde{A}^{-1}Bx\right) v_i=0, \end{aligned}$$so \(v_i^\top B\tilde{A}^{-1}Bx=0\) for \(i=1,\ldots ,j\). Now since x can be written as a linear combination of \(v_1,\ldots ,v_j\), it follows that \(x^\top B\tilde{A}^{-1}Bx=0\), and by \(\tilde{A}^{-1}\succ 0\) we have \(Bx=0\). Hence \(x^\top Bx=0\), and again by Lemma 4 we conclude that \(x=0\). Moreover,
$$\begin{aligned} L&=\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}B =\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}\tilde{A}\tilde{A}^{-1}B\\&=\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}\left( A+\lambda _* B+\alpha \sum _{l=1}^{j}Bv_lv_l^\top B\right) \tilde{A}^{-1}B \\&=\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}\bigg (\alpha \sum _{l=1}^{j}Bv_lv_l^\top B\bigg )\tilde{A}^{-1}B \quad \text{(by } \text{(25)) }\\&=\alpha \sum _{l=1}^{j}\bigg (\alpha \sum _{i=1}^{j}v_iv_i^\top B\tilde{A}^{-1}B\bigg )v_lv_l^\top B\tilde{A}^{-1}B\\&=\alpha \sum _{l=1}^{j}Lv_lv_l^\top B\tilde{A}^{-1}B=L^2, \end{aligned}$$that is, L is an idempotent matrix: indeed, it turns out that L does not depend on \(\alpha \). Therefore, for every \(v\in {\mathcal {N}}(A+\lambda _* B)\), Lv is a linear combination of \(v_1,\ldots ,v_j\), so \((v-Lv)\in {\mathcal {N}}(A+\lambda _* B)\), and from \(L(v-Lv)=Lv-L^2v=0\) it follows from the above argument, taking \(x\leftarrow v-Lv\), that \(v-Lv=0\). Hence by (26) we conclude that
$$\begin{aligned} (Bw_*+b)^\top v&=b^\top (v-Lv)=0, \end{aligned}$$as required.\(\square \)
Let us now explain how to obtain a QCQP solution \(x_*\) using Theorem 8. First when \(\lambda _*>0\), by Theorem 2\(A+\lambda _* B\) can be singular only in cases (b) and (c). First examine case (b). For the obtained \(\lambda _*\) we have \(\lambda _*>\hat{\lambda }\), so for any nonzero \(v\in {\mathcal {N}}(A+\lambda _* B)\) we have
Hence
so \(g(w_*+v)<g(w_*)\). Moreover, there exists \(x_*\) satisfying (8), so \(g(w_*)\ge g(x_*)=0\). Thus writing \(x=w_*+tv\) for \(t\in {\mathbb {R}}\), the quadratic equation in t
has a real solution \(t=\pm \sqrt{-g(w_*)/(v^\top Bv)}\). Letting t be one of these solutions, taking \(x_*=w_*+tv\) we have \(g(x_*)=0\), and from \(\lambda _*=\lambda _1\) we see that \((\lambda _*,x_*)\) satisfies (8).
Similarly, in case (c), we have \(v^\top Bv=\frac{1}{\hat{\lambda }-\lambda _*}v^\top (A+\hat{\lambda }B)v>0\) and \(0=g(x_*)>g(w_*)\) holds. Thus the quadratic equation \( g(w_*+tv)=v^\top Bvt^2+g(w_*)=0 \) in t has real solutions \(t=\pm \sqrt{-g(w_*)/(v^\top Bv)}\). Letting t be one of these solutions and taking \(x_*=w_*+tv\), we see that \((\lambda _*,x_*)\) satisfies (8).
Next when \(\lambda _*=0\) and \(A=A+\lambda _* B\) is singular, we similarly have \(g(w_*)\le 0\). However, recalling (8), when \(\lambda _*=0\) we do not need \(g(x_*)=0\), so we can directly take \(x_*=w_*\).
Summarizing the above findings, we can compute an optimal solution \(x_*\) by Algorithm 3.2. Note that the above argument clearly shows the solution can be non-unique; the goal here is to obtain one optimal solution.

3.5 Complexity
When no structure is present and A, B are dense, the dominant cost in Algorithm 3.2 lies in finding an eigenpair and the solution of a linear system; these are both \(O(n^3)\). Computing \({\mathcal {N}}(A+\lambda _*B)\) can be done by an SVD, and finding \(\gamma (\hat{\lambda })\) is mostly solving a linear system, and the other steps are all \(O(n^2)\). Hence the overall complexity of Algorithm 3.2 is \(O(n^3)\).
In comparison, the SDP-based approaches require at least \(O(n^3)\) in each iteration of the interior-point method [3] with a rather large constant, so we see that Algorithm 3.2 can be much more efficient.
Moreover, the dominant step of finding an extremal eigenpair can easily take advantage of the sparsity structure of A, B if present, resulting in running time much faster than \(O(n^3)\). This fact is illustrated in our experiments.
4 Numerical experiments
To illustrate the performance (speed and accuracy) of Algorithm 3.2 for solving QCQP (2), here we present Matlab experiments comparing with the SDP-based algorithm. Specifically, we compare Algorithm 3.2 with SDP solvers based on the interior-point method: SeDuMi [36], and SDPT3 [39], which we invoke via CVX [14]. We used the default values for parameters such as the stopping criterion. However, since the core of that algorithm and ours are both essentially the same as those for the TRS (excluding finding \(\hat{\lambda }\), which they both require), we expect that our code would outperform [24] in speed and accuracy just as in TRS.
All experiments were carried out in MATLAB version R2013a on a machine with an Intel Xeon E5-2680 processor with 64GB RAM.
4.1 Setup
We generate a “random” definite feasible QCQP with indefinite A, B as follows. First form a random positive definite \(K\succ 0\), formed as \(X^{\top }X+I\) where X is a random \(n\times n\) matrix, obtained by MATLAB’s function randn(n). Since the problem becomes ill-conditioned if K is close to singular, we chose K to have eigenvalues at least 1. We then set \(\hat{\lambda }\) to be a random positive number.
We then took a random symmetric matrix B obtained by Y = randn(n); B = Y+Y’, and define A via \(K=A+\hat{\lambda }B\). We took a and b to be random vectors.
To form a problem with known exact solution (so that the accuracy of the computed solution x can be evaluated), we take \(\lambda _\mathrm{opt}:=\hat{\lambda }+\epsilon \) where \(|\epsilon |\approx 10^{-10}\) and computed \(x_\mathrm{opt}=-(A+\lambda _\mathrm{opt}B)^{-1}(a+\lambda _\mathrm{opt}b)\), then set \(\beta \) to satisfy \(g(x_\mathrm{opt})=0\), so that \((\lambda _\mathrm{opt},x_\mathrm{opt})\) satisfies (1), hence \(x_\mathrm{opt}\) is the QCQP solution, i.e., \((\lambda _\mathrm{opt},x_\mathrm{opt}) = (\lambda _*,x_*)\).
Below we report the average speed and accuracy from 50 randomly generated instances for each matrix size n.
4.1.1 Computing \(\hat{\lambda }\)
In practice \(\hat{\lambda }\) is usually unknown in advance, and in that case our algorithm starts by computing \(\hat{\lambda }\). To this end we used the algorithm in [6, 15] to find \(\hat{\lambda }\), as discussed in Sect. 2.4.1, to obtain the interval \(D\). Although any value in \(D\) is allowed to be \(\hat{\lambda }\), we chose \(\hat{ \lambda }\) as the middle point of \(D\) to avoid ill-conditioning of \(A+\hat{\lambda }B\).
In the figures we show the performance of our algorithm in two cases: (i) when \(\hat{\lambda }\) is known a priori, shown as “Eig”, and and (ii) when \(\hat{\lambda }\) needs to be computed, shown as “Eigcheck”. In other words, the runtime of Eigcheck is the sum of Eig and finding \(\hat{\lambda }\).
4.1.2 Newton refinement process
We use a refinement process to improve the accuracy of the solution, in particular to force the computed solution to satisfy the constraint to working precision. Suppose \(\lambda _*\) is positive in (8). Then at the solution the constraint must hold with equality, but due to numerical errors this may not be the case with the computed solution x. Writing \(x=x_*+\delta \) where \(x_*\) satisfies the constraint exactly, i.e., \(g(x_*)=0\), we have
We apply Newton’s method to \(g(x)=0\) to force x to satisfy the constraint to full accuracy. Specifically, we update x by
Then
We have applied this refinement process to all three algorithms. By forcing the computed x to be numerically feasible, we rule out the misleading cases where an infeasible x with a small objective function is interpreted as a “good” solution. We note that the refinement may decrease the quality of x as a numerical solution for the problem arising in the algorithm: for example, the residual in the eigenvalue equation (22) may become larger. However, for solving the original QCQP, it is more important to improve feasibility.
4.2 Results
Figure 5 shows the runtime of the three algorithms. For \(n\ge 1000\), SDPT3 was unable to compute a solution on our computer, so we show experiments with \(n\le 700\) for this algorithm. Our algorithm and SeDuMi are able to deal with larger matrices on our machine, and we report its performance up to \(n=5000\).
We see that when \(\hat{\lambda }\) is known (Eig), our algorithm is faster than SeDuMi, SDPT3 by orders of magnitude. Even if we include the time for computing \(\hat{\lambda }\), our algorithm (EigCheck) is still faster than SeDuMi and SDPT3.
Figure 6 shows the accuracy of the computed solution. For each QCQP, let \(f_i\quad (i=1,2,3)\) be the objective value of the solution computed by each of the three algorithms. We compute
where \(f_{\text {opt}}=f(x_\mathrm{opt})\). We report the average value \(\bar{s_i}, \bar{t_i}\) of \(s_i, t_i\) for each fixed matrix size (recall that we repeated 50 random examples for each n).
Figure 6 illustrates that our algorithm found solutions and objective values nearest to optimal, hence more accurate.
Sparse matrices Another strength of our method is that it can directly take advantage of the matrix sparsity structure. Specifically, for the computation of an extremal eigenpair, which is the dominant part of our algorithm, efficient eigensolvers for large-sparse matrices are widely available [2, 22], and implemented for example in Matlab’s eigs command.
To illustrate this we generated QCQP as before, but with A, B sparse. Here we assume that \(\hat{\lambda }\) is known, and skip its computation, showing the runtime of only Eig; otherwise the code spends the majority of the runtime in finding \(\hat{\lambda }\) (unless the tridiagonal structure is fully exploited in the detection process). Similarly, SeDuMi and SDPT3 are not shown here, as their speed remained about the same as in the dense case for \(n\le 700\), hence impractical for \(n\ge 10^3\). Here we examine the runtime and accuracy of our algorithm Eig for varying matrix size n from \(10^3\) to as large as \(10^6\). We test with two types of sparse matrices: tridiagonal and random sparse (generated using MATLAB’s sprandsym).
In Figs. 7, 8 and 9 we verify that when the matrices A, B are highly sparse, our method runs faster than \(O(n^3)\); here it scaled like \(O(n^2)\) for the tridiagonal case, and also for the random sparse case when the number of nonzeros per row is fixed. The accuracy of the solution and objective values was also consistently good, as illustrated in Fig. 8 for the tridiagonal case; the other examples gave similar results.
ill-conditioned case By taking \(K=X^\top X+\varepsilon I\) for a very small \(\varepsilon >0\), K is close to singular. We took \(\varepsilon =10^0,10^{-1},\ldots ,10^{-12}\), \(n=200\) and Fig. 10 shows the results. Since the runtime did not vary significantly, we do not show the runtime. For the accuracy, we also compare with our Matlab implementation of Moré’s algorithm [24].
In Figure 10, we observe that our algorithm computed the optimal value reliably even in the ill-conditioned case, unlike the SDP-based algorithms. Moré’s algorithm gave even better accuracy here: recall that this algorithm is an extension of the classical Moré-Sorensen algorithm for TRS [35], which is iterative in nature (solving a linear system in each iteration), and not matrix-free.
5 QCQP that are not definite feasible
Thus far we have focused on the definite feasible QCQP and derived an eigenvalue-based algorithm that is fast and accurate. We now develop an analysis that accounts for “non-generic” QCQP that are not necessarily definite feasible (since the discussion in Sect. 2.1 still holds, we still focus on the strictly feasible case). The key tool for our analysis is the canonical form of a symmetric pair under congruence, which we review next.
5.1 The canonical form of (A, B) under congruence
For a pair of symmetric matrices (A, B) the canonical form under congruence [21, 37, 38], shown below, is the simplest form taken by \(W^\top (A +\lambda B )W\) where W is nonsingular. We define the \(\oplus \) operator as \(A_1\oplus A_2:=\left[ {\begin{matrix} A_1 &{} O \\ O &{} A_2 \end{matrix}} \right] \).
Theorem 9
(Lancaster and Rodman [21, Theorem 9.2.]) For symmetric matrices \(A,B\in {\mathcal {S}}^n\), there exist a nonsingular real matrix W such that
Here

when \(m>1\), and for \(m=1\),
and \(\nu _j\ne 0\), \(\delta _j,\eta _j=\pm 1\). The form in (27), (28) (29) is the canonical form of (A, B) under congruence.
This theorem shows that by congruence transformation, a symmetric matrix pair (A, B) can be block diagonalized with three types of diagonal blocks (27), (28) and (29). Each block corresponds to an eigenvalue or singular part of the pencil \(A+\lambda B\) as summarized below.
-
1.
The blocks in the right-hand side of (27) correspond to a singular part; any matrix pair that possess these blocks is singular, that is, \(\det (A+\lambda B)=0\) for every \(\lambda \).
-
2.
The blocks (28) correspond to real finite (right term) and infinite (left term) eigenvalues. The right terms are the “natural” extensions of the Jordan block in standard eigenvalue problems. \(k_j,l_j\) are the size of the Jordan blocks.
-
3.
The blocks (29) correspond to nonreal eigenvalues, which must appear in conjugate pairs. Again, \(m_j\) is the Jordan block size.
The main message of this section is that the canonical form under congruence contains full information about QCQP (2). While this work appears to be the first to use the canonical form in the analysis of QCQP, related results have been presented in the literature. The paper [9] also shows that if the matrices A, B are diagonalizable by congruence and this congruence transformation is known, the dual problem can be solved by linear programming. The preprint [16] also investigates the matrix pencil and illustrates why QCQP is nontrivial when the pencil is not simultaneously diagonalizable under congruence. Here we clarify the situation, treating extensively the difficult cases that are not definite feasible, and characterizing the feasibility/boundedness/attainability with respect to the canonical form of the pair (A, B) under congruence. The manuscript [19] shows that if the canonical form is known and the QCQP is bounded, a SOCP reformulation is possible to obtain the solution.
5.2 Implication of canonical form for QCQP boundedness
Now we turn to the implications of Theorem 9 for QCQP, first focusing on the condition for QCQP to be bounded.
In Sect. 2.1 we dealt with the case where the feasible region has no interior point, and the analysis made no assumption on definite feasibility. Hence, here we assume Slater’s condition, which allows us to invoke Lemma 1 and Theorem 1. The first observation is that the necessary condition \(A+\lambda B\succeq 0\) in (5) for QCQP to be bounded restricts the admissible canonical forms of \(A+\lambda B\) from the general form in Theorem 9 to the following.
Theorem 10
Let \(A,B\in {\mathcal {S}}^n\) be symmetric matrices. If there exists \(\lambda \ge 0\) for which \(A+\lambda B\succeq 0\), then there exists a nonsingular \(W\in {\mathbb {R}}^{n\times n}\) such that
Here \( J(\lambda ;\theta )=\left[ {\begin{matrix} 1 &{} \lambda +\theta \\ \lambda +\theta &{} 0 \end{matrix}} \right] \) for some real constant \(\theta \le 0\), and \(\eta _i=\pm 1\).
Proof
For \(A+\lambda B\succeq 0\) to hold, each block in Theorem 9 needs to be positive semidefinite. We examine each of the blocks of the form (27), (28) and (29).
First consider the block (29), corresponding to the nonreal eigenvalues. When \(m_j>1\), the (2, 2), \((2m_j,2)\), and \((2m_j,2m_j)\) elements are respectively 0, \(-\nu _j\) and 0. Thus the (29) blocks cannot be positive semidefinite, regardless of the value of \(\lambda \). Therefore we need \(m_j=1\), but then (29) is
and we look for conditions under which this is semidefinite. For this to happen we need the (1, 1) and (2, 2) elements to be nonnegative, which means we need \(\nu _j=0\), a contradiction. Thus the blocks (29) cannot exist.
Similarly, the second term in (27) cannot exist since its (1, 1), \((1,2\varepsilon _j)\), \((2\varepsilon _j,2\varepsilon _j)\) elements are respectively 0,1 and 0.
For the first term in (28), if \(k_j>1\) the \((1,k_j)\) and \((k_j,k_j)\) elements are respectively \(\delta _j\) and 0, so again we need \(k_j=1\). Then \(\delta _j(F_1+\lambda G_1)=[\delta _j]\ge 0\) so \(\delta _j=1\), and
Finally, consider the second term in (28). When \(l_j>1\) the \((1,l_j)\) and \((l_j,l_j)\) elements are respectively \(\eta _j(\lambda +\alpha _j)\) and 0, so the only value of \(\lambda \) for which \(\eta _j((\lambda +\alpha _j)F_{l_j}+G_{l_j})\succeq 0\) is \(\lambda =-\alpha _j\). Hence we need \(\eta _jG_{l_j}\succeq 0\), and the only value of \(l_j>1\) for which this holds is \(l_j=2\), in which case \(\eta _j=1\). Moreover, we need \(\lambda =-\alpha _j\) to hold simultaneously for all \(j=1,\ldots ,q\), so \(\alpha _j=\theta \) for each j (they are all the same), and by \(\lambda \ge 0\) we have \(\theta \le 0\). In addition, when \(l_j=1\) we have \(\eta _j((\lambda +\alpha _j)F_{l_j}+G_{l_j})=\eta _j(\lambda +\alpha _j)\). \(\square \)
Given A, B satisfying (30), we next examine the values of \(\lambda \) for which \(A+\lambda B\succeq 0\).
Proposition 4
Let \(A,B\in {\mathcal {S}}^n\) by symmetric matrices satisfying (30). Then the values of \(\lambda \) for which \(A+\lambda B\succeq 0\) are the intersection of
A proof is a straightforward examination of each term in (30).
The above results imply that for a bounded QCQP, the pencil \(A+\lambda B\) cannot have nonreal eigenvalues. Furthermore, Jordan blocks must be of size at most two, and when (30) contains \(q_2\ge 1\) blocks of size two \(J(\lambda ;\theta )\) (the QCQP in (6) is one such example with \(q_2=1\)), the corresponding eigenvalue \(\theta \) need to be all the same for all the \(q_2\) blocks, and moreover the value of \(\lambda \) with \(A+\lambda B\succeq 0\) is restricted to just one value, namely \(\lambda =-\theta \), corresponding to the block \(J(-\theta ;\theta )=\big [ {\begin{matrix} 1&{}0 \\ 0&{}0 \end{matrix}}\big ]\), and this value \(\lambda =-\theta \) needs to satisfy \(\bigoplus _{j=1}^{q_1}\eta _j[\lambda +\alpha _j]\succeq 0\) for \(A+\lambda B\succeq 0\) to hold.
5.2.1 Characterizing bounded QCQP via the canonical form
Recall from Lemma 1 that the QCQP is bounded if and only if there exists \(\lambda \ge 0\) such that
If (A, B) is definite so that \(A+\lambda B\succ 0\) for some \(\lambda \), then both conditions in (32) are satisfied trivially. However, these conditions are not straightforward to verify when the pair (A, B) is semidefinite but not definite.
Here we show that the conditions (32) can be written explicitly using the canonical form of symmetric pencils by congruence. Essentially this specifies the types of A, B for which the QCQP is solvable.
We start by examining the first condition in (32), the semidefiniteness of the pair (A, B). As we saw in Theorem 10, this requirement restricts the canonical form to (30); here without loss of generality we assume the \(-\alpha _j\) are arranged in nondecreasing order. Recall that \(J(\lambda ;\theta )\) is a Jordan block corresponding to a real eigenvalue, whose size is here restricted to \(2\times 2\). The so-called sign characteristics \(\eta _j\in \{1,-1\}\) must satisfy certain conditions. We separate into two cases depending on the presence of Jordan blocks.
-
if no block \(J(\lambda ;\theta )\) is present, then by Proposition 4 there exists an interval \([-\alpha _{j},-\alpha _{j+1}]\) on which \(A+\lambda B\succeq 0\), and the requirement on \(\eta _i\) is \(\eta _i=1\) for \(i\le j\) and \(\eta _i=-1\) for \(i\ge j+1\). (Note that \(\alpha _j=\alpha _{j+1}\) is allowed, in which case the interval \([-\alpha _{j},-\alpha _{j+1}]\) becomes a point. We also allow “\(\alpha _{j+1}=\infty \)”, which is when \(\eta _i=1\) for all i; this includes TRS).
-
if a block \(J(\lambda ;\theta )\) is present then the \(\theta \) values must be all the same, and \(\lambda =-\theta \) is the only value for which \(A+\lambda B\succeq 0\). The requirement on \(\eta _i\) is \(\eta _i=1\) if \(\alpha _j>\theta \), and \(\eta _j=-1\) if \(\alpha _j<\theta \). For the real and semisimple eigenvalues \(\alpha _j=\theta \), the corresponding sign characteristic \(\eta _j\) is allowed to be either 1 or \(-1\).
We repeat that in the second case the set of \(\lambda \) for which \(A+\lambda B\succeq 0\) is a point. In the first case, it is the interval \([-\alpha _{j},-\alpha _{j+1}]\). In the special case where the pair (A, B) is definite, the canonical form consists only of the second and third terms in (30) \(I_{r\times r}\oplus \bigoplus _{j=1}^{q_1}\eta _j[\lambda +\alpha _j]\), with \(\eta _j\) satisfying the first of the above conditions.
Next consider the second condition \(a+\lambda b\in {\mathcal {R}}(A+\lambda B)\). This can be written as \((A+\lambda B)x = a+\lambda b\) for some vector x, which, using the canonical form, is equivalent to
Left-multiplying \(W^{\top }\) yields
Our task is to identify the condition under which the linear system (33) has a solution x with \(A+\lambda B\succeq 0\). We consider two cases separately:
-
\(A+\lambda B\succeq 0\) on an interval \([\lambda _j,\lambda _{j+1}]\) with \(\lambda _j<\lambda _{j+1}\). In this case
$$\begin{aligned} \left( O_{u\times u}\oplus I_{r\times r}\oplus \bigoplus _{j=1}^{q_1}\eta _j[\lambda +\alpha _j]\right) W^{-1}x=W^{\top } (a+\lambda b). \end{aligned}$$This has a solution for any value of \(\lambda \in (\lambda _j,\lambda _{j+1})\) if and only if \(W^{\top } (a+\lambda b)\) is of the form
$$\begin{aligned} W^{\top } (a+\lambda b) = \begin{bmatrix} 0_{1\times u}\\*\end{bmatrix}, \end{aligned}$$(34)where \(*\in {\mathbb {R}}^{n-u}\) can take any value. Crucial here is the zero pattern of the vector \(W^{\top } (a+\lambda b)\); whether such vector exists with \(\lambda \in (\lambda _j,\lambda _{j+1})\) can be verified easily once \(W^{\top }a,W^{\top }b\) are available.
-
\(A+\lambda B\succeq 0\) only at a point \(\hat{\lambda }\). In this case (33) reduces to
$$\begin{aligned}&\left( O_{u\times u}\oplus I_{r\times r}\oplus \small \begin{bmatrix} \eta _1(\hat{\lambda }+\alpha _1)&\\ {}&\ddots&\\&\eta _{q_1}(\hat{\lambda }+\alpha _{q_1}) \end{bmatrix} \normalsize \oplus \bigoplus _{j=1}^{q_2} \begin{bmatrix} 1&\quad 0\\0&\quad 0 \end{bmatrix} \right) W^{-1}x\\&\quad =W^{\top } (a+\hat{\lambda }b). \end{aligned}$$Note that \(q_2=0\) is allowed, and otherwise \(\hat{\lambda }=-\theta \). Clearly, this has a solution if and only if
$$\begin{aligned} W^\top (a+\hat{\lambda }b) = \begin{bmatrix} O_{u\times 1}\\*\\*_J \end{bmatrix} \end{aligned}$$(35)where \(*\in {\mathbb {R}}^{n-u-2q_2}\) can take any value (except for elements corresponding to \((\hat{\lambda }+\alpha _i)=0\) if such elements are present), and \(*_J\in {\mathbb {R}}^{2q_2}\) has zeros in coordinates of even indices: \(*_J = [\star ,0,\star ,0,\ldots ,0,\star ,0]\) where each \(\star \) denotes an arbitrary scalar.
We summarize the above findings in the next theorem.
Theorem 11
A QCQP with strict interior feasible point is bounded below if and only if its canonical form under congruence is of the form (30), and \(W^{\top } (a+\lambda b)\) has nonzero structure
Note that the conditions in the theorem are straightforward to verify provided that the congruence transformation W for the canonical form is available. We note that in [19, Thm. 6] a necessary condition is given for QCQP to be bounded; Theorem 11 gives the necessary and sufficient conditions.
To compute W, in [19] an algorithm is presented assuming B is nonsingular and all the eigenvalues are real and the Jordan blocks are of size at most two with the same eigenvalue. For the general case, one can proceed by upper triangularizing the matrix pencil using the QZ algorithm (or the GUPTRI algorithm [7, 20] to deal with singular pencils), and then solving generalized Sylvester equations [12, Sec. 7.7] to block diagonalize the matrices, detect the Jordan block sizes and find the corresponding transformations for each block. Unfortunately, currently no numerically stable algorithm appears to be available for computing the canoincal form of a general symmetric pair.
5.3 Complete solution for QCQP
We now discuss how to solve a QCQP that is not necessarily definite feasible. We describe the process in a way that avoids computing the canonical form whenever possible.
5.3.1 Removing common null space
For QCQP that are not definite feasible, attempting to compute \(\lambda _*\) as in Sect. 3, we face the difficulty that the \(O_{u\times u}\) block (if it exists) forces \(\det (M_0+\lambda M_1)=0\) for every value of \(\lambda \), so the pencil is singular and hence we cannot compute \(\lambda _*\) via the generalized eigenvalue problem. Here we discuss how to remove such \(O_{u\times u}\) blocks.
Since such block corresponds to the common null space, we first compute the null space Q such that
We take Q to have orthonormal columns \(Q^\top Q=I\) and let \(Q^\perp \) be its orthogonal complement in \({\mathbb {R}}^n\). Write \(x=Q^{\perp }y+Qz\) and define \(A'=(Q^{\perp })^\top AQ^{\perp }\), \(B'=(Q^{\perp })^\top BQ^{\perp }\), \(a'=(Q^{\perp })^\top a\), \(c=Q^\top a\), \(b'=(Q^{\perp })^\top b\), and \(d=Q^\top b\). The original QCQP is equivalent to
When \(c=d=0\), this is a QCQP of smaller size with the \(O_{u\times u}\) blocks removed: the canonical form of \((A',B')\) has no zero block. Since this is simply an orthogonal transformation, it preserves the essential properties of the original QCQP, including strict feasibility.
First suppose that \(c\ne 0\) but \(d=0\). Then (36) is clearly unbounded, as we can take \(z=-\alpha c\) with \(\alpha \rightarrow \infty \).
Now suppose that \(d\ne 0\). We shall show how to obtain \((\lambda _*,x_*)\) satisfying (8) in Theorem 1. Since we assume that QCQP is bounded, \(A+\lambda _*B\succeq 0\) and \((a+\lambda _*b)\in {\mathcal {R}}(A+\lambda _*B)\) both hold and we see that
need to hold; otherwise it would not be a bounded QCQP. The first equation \(c+\lambda _*d=0\) clearly determines the value of \(\lambda _*\) (if it exists; otherwise the QCQP is unbounded), and if \(A+\lambda _*B\succeq 0\) does not hold for this \(\lambda _*\), the QCQP is unbounded. Then, taking \(y_*\) to be an arbitrary vector satisfying \((A'+\lambda _*B')y_*=-(a'+\lambda _*b')\), and defining
we have \(y_*^\top B'y_*+2b'^\top y_*+2d^\top z_*+\beta =0\), and \(x_*=Q^{\perp }y_*+Qz_*\) satisfies (8), so \(x_*\) is a global QCQP solution. Note that even when \(A'+\lambda _*B'\) is singular, by defining \(\tilde{A}\) and \(\tilde{a}\) as in Theorem 8 we can compute \(y_*\) via a nonsingular linear system.
We thus focus on QCQP without a \(O_{u\times u}\) block in what follows.
5.3.2 Solution process for nongeneric QCQP
Suppose that we have removed the common null space of A and B as in Sect. 5.3.1, and \(\hat{\lambda }\ge 0\) is known such that \(A+\hat{\lambda }B\succeq 0\). The canonical form of (A, B) must be in the form
Let the columns of V form a basis for \({\mathcal {N}}(A+\hat{\lambda }B)\), and we separate the cases depending on the eigenvalues of \(V^\top BV\). Note that the blocks in the canonical form that contribute to the null space are the blocks \(\hat{\lambda }+\alpha _j=0\) with eigenvalue \(-\alpha _j=\hat{\lambda }\), and \( J(\hat{\lambda };\theta )= \big [ {\begin{matrix} 1 &{} 0\\ 0 &{} 0 \end{matrix}} \big ] \), for which the vector \( \big [ {\begin{matrix} 0\\ 1 \end{matrix}} \big ] \) is a null vector. We denote \({\mathcal {J}}_1=\{r+j~|~\hat{\lambda }+\alpha _j=0\}\) and \({\mathcal {J}}_2=\{r+q_1+2j~|~j=1,\cdots ,q_2\}\) if \(J(\hat{\lambda };\theta )= \big [ {\begin{matrix} 1 &{} 0\\ 0 &{} 0 \end{matrix}} \big ]\), and \({\mathcal {J}}_2=\emptyset \) otherwise.
Let \({\mathcal {J}}={\mathcal {J}}_1\cup {\mathcal {J}}_2=:\{j_1,j_2,\ldots , j_{|{\mathcal {J}}_1|+|{\mathcal {J}}_2|}\}\). Denoting \(E_{{\mathcal {J}}_1,{\mathcal {J}}_2}=(e_{jl})_{j,l}\) \((1\le j\le r+q_1+2q_2, 1\le l\le |{\mathcal {J}}_1|+|{\mathcal {J}}_2|)\) by
V can be as \(V=WE_{{\mathcal {J}}_1,{\mathcal {J}}_2}U\) where U is a nonsingular matrix. Under this condition and (38),
holds. Thus we see that the zero eigenvalues of \(V^\top BV\) correspond to the terms \(J(\lambda ;\theta )\), and the nonzero eigenvalues to the terms \(\eta _j[\lambda +\alpha _j]\), and their signs are \(\eta _j\).
First we treat the case \(\hat{\lambda }>0\).
-
1.
When \({\mathcal {N}}(A+\hat{\lambda }B)=0\). This means \(A+\hat{\lambda }B\) is nonsingular and so \(A+\hat{\lambda }B\succ 0\), so it belongs to the definite feasible case, for which Algorithm 3.2 suffices.
-
2.
When \(V^\top BV\succ 0\) or \(V^\top BV\prec 0\). By (39), \(V^\top BV\succ 0\) is equivalent to \({\mathcal {J}}_2=\emptyset \), and \(\eta _j=1\) for all \(j\in {\mathcal {J}}_1\). Similarly, \(V^\top BV\prec 0\) is equivalent to \({\mathcal {J}}_2=\emptyset \) and \(\eta _j=-1\) for \(j\in {\mathcal {J}}_1\). Thus slightly perturbing \(\hat{\lambda }\) in the positive direction \(\hat{\lambda }\leftarrow \hat{\lambda }+\epsilon \) (when \(V^\top BV\succ 0\)) or the negative direction \(\hat{\lambda }\leftarrow \hat{\lambda }-\epsilon \) (when \(V^\top BV\prec 0\)) for a positive \(\epsilon \), we obtain \(W^\top (A+\hat{\lambda }B)W = I_{r\times r}\oplus \bigoplus _{j=1,j\notin {\mathcal {J}}_1}^{q_1}\eta _j[\lambda +\alpha _j\pm \epsilon ]\oplus \bigoplus _{j=1,j\in {\mathcal {J}}_1}^{q_1}[\epsilon ]\succ 0\), as long as \(\epsilon >0\) is taken sufficiently small. Thus by updating \(\hat{\lambda }\) to the perturbed \(\hat{\lambda }\), we have \({\mathcal {N}}(A+\hat{\lambda }B)=0\).
-
3.
When \(V^\top B V\) is indefinite with both positive and negative eigenvalues. For all j such that \(\hat{\lambda }+\alpha _j=0\), the signs of \(\eta _j\) take both \(+1\) and \(-1\). This implies \(\hat{\lambda }=\lambda _*\), which is the only value \(\lambda \) for which \(A+\lambda B\succeq 0\). Moreover, we can take \(v_1,v_2\in {\mathcal {N}}(A+\hat{\lambda }B)\) such that \(v_1^\top Bv_1>0,v_2^\top Bv_2<0\), so we solve \((A+\hat{\lambda }B)\hat{x}=-(a+\hat{\lambda }b)\) for \(\hat{x}\) (by (34) the QCQP is unbounded if no such \(\hat{x}\) exists) and then find \(t\in {\mathbb {R}}\) such that \(g(\hat{x}+tv_i)=0\); we choose \(i\in \{1,2\}\) depending on the sign of \(g(\hat{x})\): \(i=1\) if \(g(x_*)<0\), and \(i=2\) otherwise. Then \(x_*=\hat{x}+tv_i\) is the solution.
-
4.
When \(V^\top BV\ne O\) has a zero eigenvalue, and we have \(V^\top BV\succeq 0\) or \(V^\top BV\preceq 0\). For definiteness suppose that \(V^\top BV\succeq 0\); the other case is analogous. Since a zero eigenvalue is present, this is a case where the \(J(\lambda ;\theta )\) block exists. The goal is to find x such that \(g(x)=0\) and \((A+\hat{\lambda }B)x=-(a+\hat{\lambda }b)\). We first find a vector \(w_*\) such that
$$\begin{aligned} (A+\hat{\lambda }B)w_*=-(a+\hat{\lambda }b), \end{aligned}$$(40)while if no such \(w_*\) exists then the QCQP is unbounded by Theorem 11. Otherwise the QCQP is bounded, and we proceed to solve the unconstrained quadratic optimization problem
$$\begin{aligned} \mathop {{{\mathrm{minimize}}}}\limits _u\quad g(w_*+Vu). \end{aligned}$$(41)If the optimal objective value is 0 or below (including \(-\infty \)), there must exist \(u_0\) such that \(g(w_*+Vu_0)\le 0\). We then use a vector v such that \(v^\top Bv>0,~v\in {\mathcal {N}}(A+\hat{\lambda }B)\) and adjust a scalar t so that \(g(w_*+Vu_0+tv)= 0\). Then we obtain a global solution \(w_*+Vu_0+tv\). Next consider the case where the optimal value of (41) is larger than 0. In this case there is no x such that \(g(x)=0\) and \((A+\hat{\lambda }B)x=-(a+\hat{\lambda }b)\). Since we are dealing with the bounded case, this means we are in the unattainable case; there exists a scalar \(\mu \) such that for any \(\varepsilon >0\), there exists a feasible point x with \(f(x)=\mu +\varepsilon \). A similar statement is made in [16, Thm. 7]. Since there is no solution in this case (ii), a reasonable goal would be to provide just \(\mu \), which is the optimal objective value for
$$\begin{aligned}&\underset{\mu ,\lambda \in {\mathbb {R}}}{\mathrm{maximize}}\quad \mu \\&\mathrm{subject to}\quad \lambda \ge 0,\quad M(\lambda ,\mu )=\left[ \begin{array}{cc} \lambda \beta -\mu &{}\quad (a+\lambda b)^{\top } \\ a+\lambda b &{}\quad A+\lambda B \end{array} \right] \succeq 0 \end{aligned}$$Since \(\lambda \) is fixed to \(\lambda =\hat{\lambda }\), by the definition of \(w_*\) we see that it suffices to find the largest \(\mu \) for which
$$\begin{aligned} \left[ \begin{array}{cc} \hat{\lambda }\beta -\mu &{}\quad -((A+\hat{\lambda }B)w_*)^\top \\ -(A+\hat{\lambda }B)w_* &{}\quad A+\hat{\lambda } B \end{array} \right] \succeq 0. \end{aligned}$$We can rewrite this as
$$\begin{aligned}&\left[ \begin{array}{cc} 1 &{}\quad w_*^\top \\ 0 &{}\quad A+\hat{\lambda }B \end{array} \right] \left[ \begin{array}{cc} \hat{\lambda }\beta -\mu &{}\quad -((A+\hat{\lambda }B)w_*)^\top \\ -(A+\hat{\lambda }B)w_* &{}\quad A+\hat{\lambda } B \end{array} \right] \left[ \begin{array}{cc} 1 &{}\quad 0\\ w_*\quad &{} A+\hat{\lambda }B \end{array} \right] \\&\quad = \left[ \begin{array}{cc} \hat{\lambda }\beta -\mu - w_*^\top (A+\hat{\lambda }B)w_* &{}\quad 0\\ 0 &{}\quad (A+\hat{\lambda }B)^3 \end{array} \right] \succeq 0, \end{aligned}$$so it follows that the desired value of \(\mu \) is
$$\begin{aligned} \mu =\hat{\lambda }\beta -w_*^\top (A+\hat{\lambda }B)w_*. \end{aligned}$$(42) -
5.
When \(V^\top BV=O.\) By (39), this is the case where \(q_1=0\) and \(q_2>0.\) We proceed as above until (40). The goal is to find u such that \(g(w_*+Vu)=0\). In this case,
$$\begin{aligned} g(w_*+Vu)&= g(w_*)+2(Bw_*+b)^\top Vu + u^\top (V^\top BV)u\\&=g(w_*)+2(Bw_*+b)^\top Vu, \end{aligned}$$so \(g(w_*+Vu)\) is constant if and only if \((Bw_*+b)^\top V=0.\) If \((Bw_*+b)^\top V\ne 0\), there exists \(u_0\) such that \(g(w_*+Vu_0)=0\), which means that the global solution is \(x_*=w_*+Vu_0\). Otherwise, when \((Bw_*+b)^\top V=0\), we are unable to find u such that \(g(w_*+Vu)=0\) unless \(g(w_*)=0\). This means we are in the unattainable case, and the optimal value is as in (42).
If \(\hat{\lambda }=0\), we either have \(\lambda _*=\hat{\lambda }=0\) or \(\lambda _*>0\); the latter case (in which QCQP is definite feasible) occurs if and only if \(V^\top B V\succ 0\), because if \(V^\top B V\succeq 0\) has a zero eigenvalue, then by (38) a zero eigenvalue of \(V^\top B V\) implies the existence of \(J(\lambda ;\theta )\), which means \(D\) is a point. If \(V^\top B V\) is not positive definite, we must have \(\lambda _*=\hat{\lambda }=0\). We then compute \(w_*\) such that (40) holds, and solve (41), or more precisely a feasibility problem of finding u such that \(g(w_*+Vu)\le 0\). In fact, any \(w_*+Vu\) such that \(g(w_*+Vu)\le 0\) satisfies (8) and is therefore a global solution; recall from the complementarity condition in (8) that when \(\lambda _*=0\) it is not necessary to satisfy \(g(x_*)=0\). Such u trivially exists if \(V^\top BV\) has a negative eigenvalue. If \(V^\top BV\succeq 0\) and \(\det (V^\top BV)=0\) (i.e., \(J(\lambda ;0)\) exists) then it could be that \(\min _ug(w_*+Vu)>0\); then by Lemma 2 this corresponds to the unattainable case, with infimum value \(\mu =-w_*^\top Aw_*\) as in (42).
The steps described in this section, as shown in Fig. 11, completely solves QCQP with one constraint in the following sense:
-
1.
For any bounded QCQP, it returns the optimal (or infimum) objective value, along with its corresponding solution x if it is attainable.
-
2.
If the QCQP is unbounded, it reports unboundedness.
-
3.
If the QCQP is infeasible, it reports infeasibility.
The worst-case complexity corresponds to the case where a canonical form of (A, B) is required. Using the GUPTRI algorithm [7, 20] for the canonical form, the worst-case complexity is \(O(n^4)\). We repeat that most QCQP that are solvable in practice are solved by Algorithm 3.2, which is \(O(n^3)\) or faster.
6 Conclusion and discussion
We introduced an algorithm for QCQP with one constraint, which for generic (i.e., definite feasible QCQP for which \(\hat{\lambda }\) is known) QCQP requires computing just one eigenpair of a generalized eigenvalue problem. The algorithm is both faster and more accurate than the SDP-based approach, and can directly take advantage of the matrix sparsity structure if present.
For QCQP that are not definite feasible, for which SDP-based methods also face difficulty, we have classified the possible canonical forms under congruence of the pair (A, B), and described an algorithm (though more expensive than Algorithm 3.2) that completely solves the QCQP.
We close with remarks on future directions. First, a recent paper [34] describes an eigenvalue-based algorithm for TRS with an additional linear constraint, and a natural direction is to examine such an extension for QCQP. Second, since our algorithm essentially also solves the SDP (3), it is worth examining the class of SDP problems that can be solved similarly by an eigenvalue problem. Also of interest would be to deal with Riemannian optimization, such as minimization of \(\text{ trace }(X^{\top }AX+C^{\top }X)\) over \(X\in {\mathbb {R}}^{n\times k}\) subject to the orthogonality constraint \(X^\top X=I_k\).
References
Adachi, S., Iwata, S., Nakatsukasa, Y., Takeda, A.: Solving the trust-region subproblem by a generalized eigenvalue problem. SIAM J. Optim. 27(1), 269–291 (2017)
Bai, Z., Demmel, J., Dongarra, J., Ruhe, A., van der Vorst, H.: Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide. SIAM, Philadelphia (2000)
Ben-Tal, A., Nemirovski, A.: Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications. SIAM, Philadelphia (2001)
Boyd, S.P., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust Region Methods. SIAM, Philadelphia (2000)
Crawford, C.R., Moon, Y.S.: Finding a positive definite linear combination of two Hermitian matrices. Linear Algebra Appl. 51, 37–48 (1983)
Demmel, J., Kågström, B.: The generalized schur decomposition of an arbitrary pencil \(A- \lambda B\): robust software with error bounds and applications. Part I: theory and algorithms. ACM Trans. Math. Soft. 19(2), 160–174 (1993)
Fehmers, G.C., Kamp, L.P.J., Sluijter, F.W.: An algorithm for quadratic optimization with one quadratic constraint and bounds on the variables. Inverse Probl. 14(4), 893 (1998)
Feng, J.-M., Lin, G.-X., Sheu, R.-L., Xia, Y.: Duality and solutions for quadratic programming over single non-homogeneous quadratic constraint. J. Glob. Optim. 54(2), 275–293 (2012)
Fortin, C., Wolkowicz, H.: The trust region subproblem and semidefinite programming. Optim. Methods Softw. 19(1), 41–67 (2004)
Gander, W., Golub, G.H., von Matt, U.: A constrained eigenvalue problem. Linear Algebra Appl. 114, 815–839 (1989)
Golub, G.H., Loan, C.F.V.: Matrix Computations, 4th edn. Johns Hopkins University Press, Baltimore (2012)
Gould, N.I.M., Lucidi, S., Roma, M., Toint, P.L.: Solving the trust-region subproblem using the Lanczos method. SIAM J. Optim. 9(2), 504–525 (1999)
Grant, M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx (2014)
Guo, C.-H., Higham, N.J., Tisseur, F.: An improved arc algorithm for detecting definite Hermitian pairs. SIAM J. Matrix Anal. Appl. 31(3), 1131–1151 (2009)
Hsia, Y., Lin, G.-X., Sheu, R.-L.: A revisit to quadratic programming with one inequality quadratic constraint via matrix pencil. Pac. J. Optim. 10(3), 461–481 (2014)
Iwata, S., Nakatsukasa, Y., Takeda, A.: Global optimization methods for extended Fisher discriminant analysis. In: Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics, pp. 411–419 (2014)
Jegelka, S.: Private communication (2015)
Jiang, R., Li, D., Wu, B.: SOCP reformulation for the generalized trust region subproblem via a canonical form of two symmetric matrices. Math. Prog. (2017). https://doi.org/10.1007/s10107-017-1145-4
Johansson, S., Johansson, P.: StratiGraph and MCS Toolbox Homepage. Department of Computing Science, Umeå University, Sweden. http://www.cs.umu.se/english/research/groups/matrix-computations/stratigraph (2016)
Lancaster, P., Rodman, L.: Canonical forms for Hermitian matrix pairs under strict equivalence and congruence. SIAM Rev. 47(3), 407–443 (2005)
Lehoucq, R.B., Sorensen, D.C., Yang, C.: ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods, vol. 6. SIAM, Philadelphia (1998)
Mackey, D.S., Mackey, N., Mehl, C., Mehrmann, V.: Möbius transformations of matrix polynomials. Linear Algebra Appl. 470, 120–184 (2015)
Moré, J.J.: Generalizations of the trust region problem. Optim. Methods Softw. 2(3–4), 189–209 (1993)
Moré, J.J., Sorensen, D.C.: Computing a trust region step. SIAM J. Sci. Stat. Comput. 4(3), 553–572 (1983)
Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, New York (1999)
Pólik, I., Terlaky, T.: A survey of the s-lemma. SIAM Rev. 49(3), 371–418 (2007)
Pong, T.K., Wolkowicz, H.: The generalized trust region subproblem. Comput. Optim. Appl. 58(2), 273–322 (2014)
Rendl, F., Wolkowicz, H.: A semidefinite framework for trust region subproblems with applications to large scale minimization. Math. Program. 77(1), 273–299 (1997)
Rojas, M., Santos, S.A., Sorensen, D.C.: A new matrix-free algorithm for the large-scale trust-region subproblem. SIAM J. Optim. 11(3), 611–646 (2001)
Rojas, M., Santos, S.A., Sorensen, D.C.: Algorithm 873: LSTRS: MATLAB software for large-scale trust-region subproblems and regularization. ACM Trans. Math. Soft. 34(2), 11:1–11:28 (2008)
Sahni, S.: Computationally related problems. SIAM J. Comput. 3(4), 262–279 (1974)
Sakaue, S., Nakatsukasa, Y., Takeda, A., Iwata, S.: Solving generalized CDT problems via two-parameter eigenvalues. SIAM J. Optim. 26(3), 1669–1694 (2016)
Salahi, M., Taati, A., Wolkowicz, H.: Local nonglobal minima for solving large-scale extended trust-region subproblems. Comput. Optim. Appl. 66, 223–244 (2016)
Sorensen, D.C.: Minimization of a large-scale quadratic function subject to a spherical constraint. SIAM J. Optim. 7(1), 141–161 (1997)
Sturm, J.F.: Using SeDuMi 1.02, a Matlab toolbox for optimization over symmetric cones. Optim. Methods Softw. 11(1–4), 625–653 (1999)
Thompson, R.C.: The characteristic polynomial of a principal subpencil of a hermitian matrix pencil. Linear Algebra Appl. 14(2), 135–177 (1976)
Thompson, R.C.: Pencils of complex and real symmetric and skew matrices. Linear Algebra Appl. 147, 323–371 (1991)
Toh, K.-C., Todd, M.J., Tütüncü, R.H.: SDPT3 Matlab software package for semidefinite programming, version 1.3. Optim. Methods Softw. 11(1–4), 545–581 (1999)
Vavasis, S.A.: Quadratic programming is in NP. Inf. Process. Lett. 36(2), 73–77 (1990)
Acknowledgements
We thank Satoru Iwata and Akiko Takeda for comments on an early draft, and Françoise Tisseur for a fruitful discussion on detecting definite matrix pairs and sharing with us the MATLAB code for [15]. We gratefully acknowledge the referees for their constructive comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by JSPS Scientific Research Grants Nos. 26540007 and 26870149. YN is supported as a JSPS Overseas Research Fellow.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Adachi, S., Nakatsukasa, Y. Eigenvalue-based algorithm and analysis for nonconvex QCQP with one constraint. Math. Program. 173, 79–116 (2019). https://doi.org/10.1007/s10107-017-1206-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-017-1206-8