Abstract
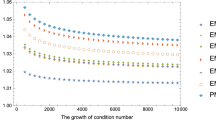
An interval extension of successive matrix squaring (SMS) method for computing the weighted Moore–Penrose inverse \(A^{\dagger }_{MN}\) along with its rigorous error bounds is proposed for given full rank \(m \times n\) complex matrices A, where M and N be two Hermitian positive definite matrices of orders m and n, respectively. Starting with a suitably chosen complex interval matrix containing \(A^{\dagger }_{MN}\), this method generates a sequence of complex interval matrices each enclosing \(A^{\dagger }_{MN}\) and converging to it. A new method is developed for constructing initial complex interval matrix containing \(A^{\dagger }_{MN}\). Convergence theorems are established. The R-order convergence is shown to be equal to at least l, where \(l \ge 2\). A number of numerical examples are worked out to demonstrate its efficiency and effectiveness. Graphs are plotted to show variations of the number of iterations and computational times compared to matrix dimensions. It is observed that ISMS is more stable compared to SMS.










Similar content being viewed by others
References
Alefeld, G., Herzberger, J.: Introduction to Interval Computation. Academic press, London (2012)
Ben-Israel, A., Greville, T.N.: Generalized Inverses: Theory and Applications, vol. 15. Springer Science & Business Media, Berlin (2003)
Ilić, Dragana S.Cvetković, Wei, Yimin: Algebraic Properties of Generalized Inverses. Springer, Berlin (2003)
Bojanczyk, A., Higham, N.J., Patel, H.: Solving the indefinite least squares problem by hyperbolic QR factorization. SIAM J. Matrix Anal. Appl. 24(4), 914–931 (2003)
Chen, L., Krishnamurthy, E., Macleod, I.: Generalised matrix inversion and rank computation by successive matrix powering. Parallel Comput. 20(3), 297–311 (1994)
Esmaeili, H., Pirnia, A.: An efficient quadratically convergent iterative method to find the Moore–Penrose inverse. Int. J. Comput. Math. 94(6), 1079–1088 (2017)
Li, Z., Sun, J.: Mixed and componentwise condition numbers for weighted Moore–Penrose inverse and weighted least squares problems. Filomat 23(1), 43–59 (2009)
Lin, L., Lu, T.T., Wei, Y.: On level-2 condition number for the weighted Moore–Penrose inverse. Comput. Math. Appl. 55(4), 788–800 (2008)
Frommer, A., Hashemi, B., Sablik, T.: Computing enclosures for the inverse square root and the sign function of a matrix. Linear Algebra Appl. 456, 199–213 (2014)
Ma, J., Qi, L., Li, Y.: The representations and computations of generalized inverses \({A}^{(1)}_{TS}\), \({A}^{(1,2)}_{TS}\) and the group inverse. Calcolo 54(4), 1147–1168 (2017)
Sheng, Xingping: Computation of weighted Moore–Penrose inverse through Gauss–Jordan elimination on bordered matrices. Appl. Math. Comput. 323, 64–74 (2017)
Martins, M.: Some improvements on the convergence of the interval Maor method. Int. J. Comput. Math. 74(4), 493–507 (2000)
Miladinović, M., Miljković, S., Stanimirović, P.: Modified SMS method for computing outer inverses of Toeplitz matrices. Appl. Math. Comput. 218(7), 3131–3143 (2011)
Moore, R.E.: Methods and Applications of Interval Analysis. SIAM, Philadelphia (1979)
Neumaier, A.: Interval Methods for Systems of Equations, vol. 37. Cambridge University Press, Cambridge (1990)
Oseledets, I.V., Tyrtyshnikov, E.E.: Approximate inversion of matrices in the process of solving a hypersingular integral equation. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki 45(2), 315–326 (2005)
Petkovic, M.D., Petkovic, M.S.: Iterative methods for the inclusion of the inverse matrix. arXiv preprint arXiv:1406.5343 (2014)
Petković, M.D., Stanimirović, P.S., Tasić, M.B.: Effective partitioning method for computing weighted Moore–Penrose inverse. Comput. Math. Appl. 55(8), 1720–1734 (2008)
Potra, F.: On Q-order and R-order of convergence. J. Optim. Theory Appl. 63(3), 415–431 (1989)
Rump, S.M.: INTLAB–INTerval LABoratory. In: Cesndes, T. (ed.) Developments in Reliable Computing, pp. 77–104. Kluwer Academic Publishers, Dordrecht (1999)
Rump, S.M.: Verification methods: rigorous results using floating-point arithmetic. Acta Numer. 19, 287–449 (2010)
Rump, S.M., Graillat, S.: Verified error bounds for multiple roots of systems of nonlinear equations. Numer. Algorithms 54(3), 359–377 (2010)
Ullah, M.Z., Soleymani, F., Al-Fhaid, A.S.: An efficient matrix iteration for computing weighted Moore–Penrose inverse. Appl. Math. Comput. 226, 441–454 (2014)
Soheili, A.R., Soleymani, F., Petkovic, M.D.: On the computation of weighted Moore–Penrose inverse using a high-order matrix method. Comput. Math. Appl. 66(11), 2344–2351 (2013)
Saraev, P.V.: Interval pseudo-inverse matrices and interval Greville algorithm. Reliab. Comput. 18, 147–156 (2013)
Sheng, X., Chen, G.: A note of computation for MP inverse \(A^{\dagger }\). Int. J. Comput. Math. 87(10), 2235–2241 (2010)
Stanimirović, P.S., Cvetković-Ilić, D.S.: Successive matrix squaring algorithm for computing outer inverses. Appl. Math. Comput. 203(1), 19–29 (2008)
Van Loan, C.F.: Generalizing the singular value decomposition. SIAM J. Numer. Anal. 13(1), 76–83 (1976)
Wang, H., Cao, D., Liu, H., Qiu, L.: Numerical validation for systems of absolute value equations. Calcolo 54(3), 669–683 (2017)
Wei, Y.: Successive matrix squaring algorithm for computing the Drazin inverse. Appl. Math. Comput. 108(2), 67–75 (2000)
Wei, Y., Wu, H., Wei, J.: Successive matrix squaring algorithm for parallel computing the weighted generalized inverse \(A^{\dagger }_{ MN}\). Appl. Math. Comput. 116(3), 289–296 (2000)
Zhang, N., Wei, Y.: A note on the perturbation of an outer inverse. Calcolo 45(4), 263–273 (2008)
Zhang, X., Cai, J., Wei, Y.: Interval iterative methods for computing Moore–Penrose inverse. Appl. Math. Comput. 183(1), 522–532 (2006)
Chen, Y., Shi, X., Wei, Y.: Convergence of Rump’s method for computing the Moore–Penrose inverse. Czechoslov. Math. J. 66(3), 859–879 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
Third author gratefully acknowledges support from the Research Project 174013 of the Serbian Ministry of Science.
Rights and permissions
About this article
Cite this article
Roy, F., Gupta, D.K. & Stanimirović, P.S. An interval extension of SMS method for computing weighted Moore–Penrose inverse. Calcolo 55, 15 (2018). https://doi.org/10.1007/s10092-018-0257-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10092-018-0257-4
Keywords
- Weighted Moore–Penrose inverse
- Successive matrix squaring method
- Interval arithmetic
- Interval iterative method
- Order of convergence