Introduction

Self-tapping screw (STS) has higher strength and stiffness compared with traditional screw as it is made of stronger steel, hardened threads [1, 2] and a little bit larger ratio of nominal thread and shank diameter [2]. Due to this excellent performance, STS obtained higher status and broader reputation in various countries as a new-era’s multi-purposes fastener.

One of the representative uses of STS is for high-performance tensile splice timber joints. In this aspect, in 2001, Blass and Bejtka [1] first clarified experimentally that the wood-to-wood tensile single shear joint composed of inclined STS with angle of 60° between screw axis and loading direction showed 1.5 times load-carrying capacity of that of traditional 90° tensile single shear joint. In 2002, they further proposed theoretical equations [3] for predicting load carrying capacity of the inclined STS joint by taking the effect of yielding and embedment of screw into considerations based on Johansen theory [4]. In the same year, Kevarinmäki [5] proposed design equations for withdrawal strength and stiffness of wood-to-wood as well as LVL-to-LVL inclined STS tensile single shear or/and X-shear (both tensile and compressive) joint without considering the effect of yielding and embedment of screw based on the existing European standard [6]. In 2006, Tomasi et al. [7] presented experimental and numerical results of the static, as well as push–pull cyclic loading test on wood-to-wood inclined STS X-shear joint including traditional 90° shear joints for clarifying ductility of STS timber joints. In Chile, Opazo and Bustos [8] confirmed applicability of Bejtka and Blass model [3] to the inclined STS tensile single shear joints made of Chile-grown radiate pine. After these pioneering researches, a lot of researches for making sure the maximum load carrying capacity [2, 9,10,11,12,13,14,15,16,17] as well as stiffness [12,13,14,15,16,17] of inclined STS wood-to-wood shear joint as well as steel-to-wood joint [9, 11] have been carried out until today.

Next important role of STS might be for reinforcing inferior strength properties of timber. In this aspect, various researches have also been reported up to recently [18,19,20,21,22,23,24].

Among various usages of STS mentioned above, in this article, we paid our attention to mainly the withdrawal performance of STS and aimed to make a wooden parallel chord truss specimen whose mechanical performance is controlled in some extents by changing the number of STS to be used for connecting chord and web member at each nodal point.

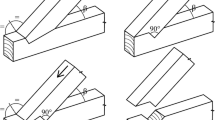
The basic idea of wooden parallel chord truss that gave useful hints to this study was originally given by H.J. Blass in the WCTE2012 [25] as shown in Fig. 1. In the original idea [25], the joint between chord and tensile web was designed by glued-in-threaded steel rod penetrated into perpendicular layer of CLT to obtain ductile performance [26]. The joint between chord and compressive web was composed of the step-joint which is a kind of traditional European carpentry joint by making use of wood-to-wood contact or/and interlocking action.

Fig. 1
figure 1

Concept of glulam parallel chord truss introduced by Blass [28]. (Image was drawn by K. Komatsu based on the original image by Blass [28])

Full size image

While in this study, multiple STS were selected for composing all nodal point joints. One of the reasons we chose STS was that using STS was thought to be easier for making parallel chord truss specimens by non-professional peoples than using glued-in-threaded steel rod for the tensile joint or using step joint for compressive joint. The second reason was that multiple STS could change the performance of nodal point in some extents by adjusting the number or allocation of STS in the nodal point. From the reasons mentioned above, our final research purpose was not to create an efficient wooden parallel chord truss but to verify our nonlinear analysis method using wooden parallel chord truss specimens whose nodal point performances are intentionally adjusted so as to show the various nonlinear behaviors.

Materials and methods

Configurations of parallel chord trusses

The configuration of wooden parallel chord truss was determined to have a span length of 1900 mm and a depth between top-chord and bottom-chord of 296 mm subject to a central point loading as shown in Fig. 2a. The main reason to choose this configuration was due to the capacity of the testing machine that could be used for this study. Fig. 2b emphasizes the difference of kind, number and allocation of STS at nodal point.

Fig. 2
figure 2

Wooden parallel chord trusses designed and tested in this study

Full size image

Number of STS per nodal point was set as the experimental parameter starting from 2rows-2lines (total 4STS) until 2rows-4lines (total as 8STS). As sufficient cross-sectional area was required to penetrate multiple STS into the nodal point, diagonal member was designed as “composite web” using double 38 mm by 89 mm solid Canadian spruce lumbers with nail-glued 12 mm plywood for a spacer shim as shown in the drawing at right edge of Fig. 2a. Using this type of wider cross-sectional web member, multiple STS could be penetrated into the nodal point.

The tensile nodal joints were all composed of multiple longer STS of 140 mm length, while the compressive nodal joints were composed of shorter STS of 80 mm length. The first specimen IST-2-1 was fabricated using partially threaded STS having 8 mm diameter as a trial. IST-2-2, IST-3-1, IST-4-1 and IST-4-2 specimens were fabricated using full-threaded STS of 5 mm diameter.

The difference between IST-4-1 and IST4-2 was on the allocation of STS at nodal point. Allocations of 4lines STS in IST-4-1 specimen were staggered 1.0d apart as shown in Fig. 2b, while those of IST-4-2 specimen were staggered 2.6d apart as shown in Fig. 2b, in which “d” was the nominal diameter of STS.

The distance between nodal points at central part of upper chord was 350 mm and this was 50 mm longer than other part (300 mm) to avoid concentration of multiple STS in the bottom tensile nodal point at mid-span, therefore, location of struts at both supports were shifted to outside by 19 mm as shown in Fig. 2a. Replication of each truss specimen was one.

Materials

Chord, part of web and strut

Canadian spruce (Picea glauca (Moench) Voss) 2 by 4 dimension lumbers, having the nominal cross section of 38 × 89 mm, imported from Canada, were used for all chord members, struts and outer parts of composite web members. Larch plywood of 12 mm thickness produced in China was used for the inner part of the composite web member.

Modulus of elasticity of materials was measured using the 4-points edgewise bending test with 1600 mm span length (18 times of member height) in accordance with Chinese standard GB/T 50329 [27] before truss specimens were fabricated. Density and moisture contents of materials were measured on the 20 mm cubic specimens taken from destroyed parallel chord truss specimens in accordance with GB/T 1933 [28] and GB/T 1931 [29], respectively. Table 1 shows mean values of the mechanical and physical properties of members used in the parallel chord truss specimens.

Table 1 Mechanical and physical properties of members used in parallel chord truss specimens
Full size table

Composite web

Diagonal web members were composed of double 2 by 4 edgewise solid lumbers sandwiching with single plywood shim to obtain enough cross-sectional area for penetrating multiple STS. Assembly of solid lumbers and plywood was done using a vinyl acetate resin emulsion adhesive and several short screws to obtain a perfect composite cross-section. The apparent modulus of elasticity of the composite web members \({E_{{\text{comp}}}}\)is derived in Eq. (1) assuming that the three parallel members could share a common deformation due to perfect adhesive joint with each other.

$${E_{{\text{comp}}}}=\left( {\frac{{2{E_{{\text{CS}}}} \cdot {A_{{\text{CS}}}}+{E_{{\text{PW}}}} \cdot {A_{{\text{PW}}}}}}{{{A_{{\text{web}}}}}}} \right){\text{ }}$$
(1)

where, \({E_{{\text{CS}}}}\) modulus of elasticity of Canadian spruce 2 by 4 lumber [N/mm2], \({E_{{\text{PW}}}}\) modulus of elasticity of edgewise plywood [N/mm2], \({A_{{\text{CS}}}}\) area of single Canadian spruce member [mm2], \({A_{{\text{PW}}}}\) area of plywood member [mm2], \({A_{{\text{web}}}}\) area of composite web member (= 2 \({A_{{\text{CS}}}}\) + \({A_{{\text{PW}}}}\)) [mm2].

STS

In this study, two different kinds of STS were used. For IST-2-1 specimen (first trial specimen), partial threaded STS having a nominal diameter of 8 mm and length of 80 mm and 140 mm made in China were used. For IST-2-1, IST-3-2, IST-4-1 and IST-4-2 specimens, full-threaded STS having nominal diameter of 5 mm and length of 80 mm and 140 mm made in Italy were used. Fig. 3a, b show photos of screws used in this study.

Fig. 3
figure 3

STS used in this study

Full size image

Measurements of deflection, relative slip and strain in truss specimen

To record the flexural behaviour of wooden parallel chord truss, load–deflection relationship at mid-span, axial force–slip relationship between chord and diagonal web, member strains relating to the estimation of eccentric moment at nodal points were measured using a load-cell, deflection measuring devices, and strain gauges at the locations shown in Fig. 4a–c.

Fig. 4
figure 4

Locations and numbering of measuring devices

Full size image

Eccentric moment caused by continuity of chord and eccentric allocations of nodal points was tried to measure by a pair of strain gauges glued on the lower surface and on the 5.5 mm inner side surface of the target point along chord member as shown in Fig. 4c and moment is estimated by Eq. (2).

$$M=\frac{1}{2}({\varepsilon _{{\text{upper}}}} - {\varepsilon _{{\text{lower}}}}) \cdot {Z_{{\text{chord}}}} \cdot {E_{{\text{chord}}}}$$
(2)

where, \({\varepsilon _{{\text{upper}}}}\) strain at upper surface = \(\left( {\frac{{38/2}}{{38/2 - 5.5}}} \right) \cdot {\varepsilon _{{\text{side}}}}\) = \(1.4 \cdot {\varepsilon _{{\text{side}}}}\), \({\varepsilon _{{\text{side}}}}\): strain measured at 5.5 mm inner side surface of chord (refer to Fig. 4c), \({\varepsilon _{{\text{lower}}}}\) strain measured at lower surface, \({Z_{{\text{chord}}}}\) section modulus of chord member (mm3), \({E_{{\text{chord}}}}\) modulus of elasticity of chord member (N/mm2).

Figure 5 shows a feature of testing machine, test set-up and data acquisition system used in this study. All tests were executed under a monotonic loading protocol with a cross-head speed of 2 mm/minutes.

Fig. 5
figure 5

Feature of testing machine, test set-up and data acquisition system used in this study

Full size image

Fundamental joint test of nodal point

After the destructive experiments on the parallel chord trusses were finished, fundamental joint tests of the nodal point were done using chord materials taken from undamaged parts of destructed specimens and adding new Canadian spruce 2 by 4 lumbers as the diagonal web member. The line number of STS per row in the joint varied from 1 to 4 as the experimental parameter. Specifications of the fundamental joint test are tabulated in Table 2. In the case of fundamental joint test, diagonal web was not the composite section but single solid lumber was used. Fig. 6a, b show outline of the fundamental joint tests in the case of 4lines STS (VT4 and VC4 specimens) as examples. Replication of each joint test specimen was three.

Table 2 Specifications on the fundamental joint tests (replication numbers: 3)
Full size table
Fig. 6
figure 6

Fundamental joint test of nodal point

Full size image

Finite element method

Chord–web joints

Nonlinear behaviour of test specimens was analyzed using a FEM program [30]. In the program, chord–web joints were modeled as nonlinear axial springs. Transmissions of shear force and moment between chord and diagonal web member were not considered. Force–slip relationships of the spring used in tensile and compressive joints were expressed by a tetra polygonal-line approximation model which was packaged in the FEM program [30]. All parameters necessary for describing the tetra polygonal-line approximation model were determined so as to fit the average force–slip curves obtained from the fundamental joint tests. Fitting operations were done based on the visual decisions of the first named author.

Material nonlinearity of chord member

Material nonlinearity was considered only in the chord members by employing fiber model [31, 32] which was installed at both nodal points of chord element so as to have a length of h/2 (h is depth of member, and quantity of h/2 was recommended in the program [30]) as shown in Fig. 7. Strain in a fiber slice was expressed using curvature \({\phi _x}\), axial strain \({\varepsilon _0}\), and coordinate value of i-th fiber slice \(({y_i},{z_i})\) as shown in Fig. 7. Using the fiber model, axial and bending interacting stress was automatically evaluated.

Fig. 7
figure 7

Element with fiber slices at both nodal point I and J

Full size image

Stress–strain relationship in a fiber slice of Canadian spruce was deduced as follows;

  1. 1.

    Modulus of rapture Fb and compressive strength parallel to the grain Fc were presumed via specific gravity G of chord member based on the regression Eqs. (3) and (4) which were presented in US Wood Handbook [33].

$${F_b}=170.7 \cdot {G^{1.01}}$$
(3)
$${F_c}=93.7 \cdot {G^{0.97}}$$
(4)
  1. 2.

    Tensile strength Ft was presumed based on the widely used ratio [34,35,36,37] between bending strength and tensile strength.

$${F_t}=0.6 \cdot {F_b}$$
(5)
  1. 3.

    Compressive proportional limit stress Fy was presumed based on the research results of Sawada [37].

$${F_y}=0.79 \cdot {F_c}$$
(6)
  1. 4.

    Strain at maximum compressive strength was presumed based on the research results of Sawada [37].

$${\varepsilon _0}=1.1764 \cdot \left( {\frac{{{F_c}}}{E}} \right)$$
(7)

From the above-mentioned assumptions, stress–strain relationship of fiber slice of Canadian spruce will be able to be described schematically as shown in Fig. 8. In the tensile stress–strain region, after stress value reached at Ft, tensile stress was controlled so as to decrease toward the target strain of 30Ft/E.

Fig. 8
figure 8

Schematic diagram of stress–strain relationship of fiber slice

Full size image

Results and discussion

Validity of stress–strain relationship used in the fiber model

Validity of stress–strain relationship used in the fiber model was evaluated by comparing FEM simulation result and experimental raw data provided by the Canadian research team. The Canadian experiment was done by flat-wise three points bending test method with 20 h span length (h: beam depth) on Canadian SPF 2 by 4 dimension lumbers whose average specific gravity was 0.47 and average MOE was 10.5 MPa. Figure 9 shows comparison between FEM simulation (solid line with markers) and experimental 10 results (dashed lines). FEM calculation was done using a simplest 2-elements FEM model whose mechanical properties were deduced by Eqs. (3) to (7) via given specific gravity and MOE subject to a central incremental deflection of -0.001 mm. As good agreement was recognized, the same estimation method for the material properties of chord members was applied to each FEM model for the parallel chord truss tested.

Fig. 9
figure 9

Comparisons between FEM simulation and experimental result

Full size image

Results of fundamental joint tests

Fig. 10a, b show results of fundamental joint test and tetra polygonal-line fitting situations.

Fig. 10
figure 10

Results of fundamental joint test and tetra polygonal-line fitting situations. Note Dashed lines indicate averaged lines of three experimental curves

Full size image

Except DT2 specimen, initial slip region of all tensile joints showed almost less than 1 mm, and after exceeded maximum value, load carrying capacity decreased steeply until almost half of the maximum value, then slowly decreased once again. As the STS used for DT2 specimen had trumpet-shaped wider screw head as shown in Fig. 3a, pull-through resistance by screw head was remarkable so that DT2 only showed large deformation ability without load reduction until 18 mm slip as shown in Fig. 10a and finally splitting failure occurred at chord member. On the other hand, STS used for VT specimens had cylinder-shaped slender screw head as shown in Fig. 2b. Hence pull-through resistance of screw head was not so expected like the case of DT2 and both withdrawal of threaded part from web member and embedment of cylinder head into chord member were occurred until loading was stopped. Due to this configurational difference, characteristic load–slip curves of these two types of joint specimens were appeared. For the tensile joint specimens, the increase of number of screw, as well as pitch in staggered allocation, clearly made initial stiffness and maximum strength increased. The effect of those was much larger for the stiffness than the strength.

While in the case of compressive joint, initial slip region was 2–3 mm then showed gradual load increasing region until maximum value. After reaching the maximum value, load decrease was not so steep like tensile joint. Load reduction occurred due to pushing out of edge-side timber by an inner bent STS as sliding down movement of web member increased. Some specimens finally failed by sprit at the edge-side surface.

As the actual joints at all nodal points of test specimens had 2rows-multi (2–4) lines STS allocations, all load values determined in the tetra polygonal-line approximations were multiplied by 20.9 = 1.866 in accordance with the rule in Eurocode 5 [38].

Comparisons between experimental observations and FEM calculations

Definitions of axial forces and nodal moments

Figure 11 shows definitions of axial forces and nodal point moments in the left-half side of parallel chord truss analyzed. In this figure, \({F_i}\) (i = 1–4) is axial force in the chord member, \({N_i}\) (i = 0–4) is axial force in the diagonal web member and strut, \({M_i}\) (i = 2–10) is eccentric moment at nodal point which is thought to be caused by continuity of chord member and also eccentric allocations of modal points.

Fig. 11
figure 11

Definitions of axial force and nodal point moments in the parallel chord truss analyzed

Full size image

Axial forces in members

Comparisons between axial forces observed by strain gauges and those calculated by FEM could be done only in the case of IST-2-1specimen (first trial specimen), because strain gauges for measuring axial forces in chord and web member were only put on the IST-2-1 specimen as shown in Fig. 4a.

Figures 12 and 13 show these comparisons. Agreements between observed axial forces in members (dashed lines) and calculated values (solid line with marker) are almost good except the case of compressive force N2 in the diagonal web as shown in Fig. 13.

Fig. 12
figure 12

Axial forces observed (dashed line) and those calculated by FEM (solid line with markers) in chord members

Full size image
Fig. 13
figure 13

Axial forces observed (dashed line) and those calculated by FEM (solid line with markers) in diagonal web members

Full size image

Bending moment at nodal points

As the absolute values of bending moments at nodal points measured by a pair of strain gauge were almost half of those calculated by FEM, we judged that results of the observed moment were not enough for presenting in this article. This might be a limitation on the accuracy of strain gauge put on this kind of strain field where strain values vary steeply within relatively short region.

Load–deflection, slip at nodal points, fiber stress and final failure phenomena

Figures 14, 15, 16, 17 and 18 show nonlinear behaviors of each test specimen separately. Comparisons between observed load–deflection relationship (solid line) and computed ones (dotted line) including most critical fiber stress (dashed line) as well as observed slip at nodal points (dashed line) and computed ones (solid line with markers) accompanying with photo showing final failure phenomena are to be shown at the same time to understand the interactive effects from both joint performance and material nonlinearity. Locations of slip measuring device Ri are shown in Fig. 4a, b.

Fig. 14
figure 14

Nonlinear behaviors of IST-2-1 specimen

Full size image
Fig. 15
figure 15

Nonlinear behaviors of IST-2-2 specimen

Full size image
Fig. 16
figure 16

Nonlinear behaviors of IST-3-1 specimen

Full size image
Fig. 17
figure 17

Nonlinear behaviors of IST-4-1 specimen

Full size image
Fig. 18
figure 18

Nonlinear behaviors of IST-4-2 specimen

Full size image
IST-2-1 specimen

As IST-2-1 specimen composed of partially threaded STS whose tensile load–slip relationship was peculiar as seen in Fig. 10a, it showed clear nonlinear behavior from lower applied load level as can be seen from Fig. 14a as the STS had especially lower yield strength. Fig. 14b shows good agreement between observed slip and calculated one was obtained until P reached at 20 kN. Fig. 14a, b show that stress level of the most critical fiber slice was about 67% of its failure level (ft = 0.67Ft) at P = 20 kN level. Afterwards, as the actual tensile joint had already reached to its maximum pull-out capacity, fatal pull-out of STS occurred by accompanying with bottom chord bending failure as shown in Fig. 14c although FEM continued calculation as if there was still some safety margin in tensile joint capacity.

IST-2-2 specimen

Fig. 15b describes that when P reached at 20 kN, tensile nodal joint of IST-2-2 specimen was largely pulled out so that stress distribution in the bottom chord changed drastically hence stress in the most critical fiber slice in the bottom chord suddenly rose up to its critical value (ft=Ft) as shown in Fig. 15a. Afterwards, bending failure phenomena gradually progressed as shown in Fig. 15a, c. FEM could qualitatively predict these phenomena well, but could not do quantitatively well.

IST-3-1 specimen

Fig. 16a–c describe the nonlinear behaviors of ITS-3-1 specimen. The nonlinear behaviors of this specimen are similar to those of ITS-2-2. Namely, when P reached at 29 kN, tensile nodal joint was largely pulled out so that bottom chord subjected to mostly compressive force due to re-distribution of axial force, afterward bottom chord fiber slice reached its critical value (ft = Ft) when δ reached at 27 mm, then bending failure progressed gradually as shown in Fig. 16a and finally load carrying capacity of bottom chord was lost. FEM could qualitatively predict these phenomena very well but not quantitatively perfect.

IST-4-1 specimen

ITS-4-1 specimen behaved quite differently from FEM prediction. As can be seen from Fig. 17b, in this specimen, tensile joint was not pulled-out largely even when P reached 30 kN. While at this instant, fiber stress at bottom of mid-span once reached to its critical value (ft = Ft) but soon stress decreased till about ft=0.82Ft and this level was kept until δ reached to 60 mm. During this term, the so-called “plug-shear” failure occurred at a tensile joint in the bottom chord near the mid-span as shown in Fig. 17c due to 1.0d narrow staggered allocation of STS as shown in Fig. 2b. In consequence, FEM predicted a kind of bi-linear rising load–deflection curve while reality on specimen was quite different as shown in Fig. 17a, c. Fiber model used could not correspond against “plug-shear” failure at all.

IST-4-2 specimen

In the case of IST-4-2 specimen, STS allocation was staggered with 2.6d (d is screw diameter) apart as shown in Fig. 2b so that no more “plug-shear” failure occurred. Failure mode was a pure tensile failure in the bottom chord member near the mid-span as shown in Fig. 18c. In this specimen, pull-out of the tensile nodal joint was scarcely observed as shown in Fig. 18b. Therefore, the cause of nonlinear behaviors was entirely due to material nonlinearity. Stress in the most critical fiber slice near the mid-span once it reached nearly its critical value ft = Ft when P reached at 30kN, afterward, pure tensile failure occurred by rising up of tensile stress, although FEM did not predict so rigorously.

Comparisons among five specimens

Figure 19 shows load–deflection curves observed on the five different truss specimens. In this section, comparisons are to be done based on this figure.

Fig. 19
figure 19

Comparisons among five different trusses

Full size image

Comparing IST-2-1 and IST-2-2, although both were composed of same numbers of STS but having different thread profiles, it can be seen that IST-2-1 showed lower stiffness due to less threaded part length but very rich ductility due to embedment resistance of trumpet-shaped screw head.

Comparisons among IST-2-2, IST-3-1 and IST-4-2, having a proportional number of STS with sufficient space with each other, imply that stiffness and strength were likely to be simply proportional to the numbers of STS used for composing nodal joints.

Comparing IST-4-1 and IST-4-2, although both were composed of same numbers of STS but having different space of staggered allocations, it was clear that performance of IST-4-1 was inferior to that of IST-4-2 because IST-4-1 was staggered with 1.0d apart, while IST-4-2 was staggered with 2.6d apart, consequently there was a large difference between IST4-1 and IST4-2 on stiffness, failure phenomenon and strength.

Summaries

From experimental and numerical investigations on wooden parallel chord truss composed of STS, following findings might be summarized.

  1. 1.

    Agreements between observed axial forces measured by strain gauges and those of calculated by FEM were good, although there were some discrepancies.

  2. 2.

    Using tetra polygonal-line approximation models for nonlinear load–deformation relationship of joint spring in FE-Model, slip behaviors at nodal points of wooden parallel chord trusses were reasonably expressed.

  3. 3.

    Implementation on the nonlinear behaviors of wooden parallel chord trusses was done using both observed results and FEM results. In some extent, this approach could explain nonlinear behaviors reasonably. In the final stage of the failure, however, predicting abilities of FEM were not enough probably due to insufficient information about failure criteria of Canadian spruce used in the experiments.

  4. 4.

    Numbers of STS composing nodal joint were simply proportional to the stiffness and strength of wooden parallel chord trusses.

  5. 5.

    Material nonlinearity gave less effect on the total nonlinear behaviour of the specimens when joint performance was inferior, on the other hand, as the joint performance increased material nonlinearity gave dominant effect on the total nonlinear behaviour of the specimens.