Evaluating landslide susceptibility based on cluster analysis, probabilistic methods, and artificial neural networks

Abstract

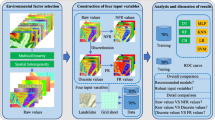
In this study, the cluster analysis (CA), probabilistic methods, and artificial neural networks (ANNs) are used to predict landslide susceptibility. The Geographic Information System (GIS) is used as the basic tool for spatial data management. CA is applied to select non-landslide dataset for later analysis. A probabilistic method is suggested to calculate the rating of the relative importance of each class belonging to each conditional factor. ANN is applied to calculate the weight (i.e., relative importance) of each factor. Using the ratings and the weights, it is proposed to calculate the landslide susceptibility index (LSI) for each pixel in the study area. The obtained LSI values can then be used to construct the landslide susceptibility map. The aforementioned proposed method was applied to the Longfeng town, a landslide-prone area in Hubei province, China. The following eight conditional factors were selected: lithology, slope angle, distance to stream/reservoir, distance to road, stream power index (SPI), altitude, curvature, and slope aspect. To assess the conditional factor effects, the weights were calculated for four cases, using 8 factors, 6 factors, 5 factors, and 4 factors, respectively. Then, the results of the landslide susceptibility analysis for these four cases, with and without weighting, were obtained. To validate the process, the receiver operating characteristics (ROC) curve and the area under the curve (AUC) were applied. In addition, the results were compared with the existing landslide locations. The validation results showed good agreement between the existing landslides and the computed susceptibility maps. The results with weighting were found to be better than that without weighting. The best accuracy was obtained for the case with 5 conditional factors with weighting.

Appendices

Appendix 1. A brief introduction to two-step cluster analysis

The cluster analysis is a widely used unsupervised learning technique for identifying different patterns in datasets. The goal of the cluster analysis is to allocate objects into groups whose members are similar in some way (Kaufman and Rousseeuw 1990). The k-means, hierarchical, non-hierarchical, expectation-maximization and two-step are some of the techniques used in cluster analysis. The two-step cluster analysis (TSCA) is an algorithm primarily designed to analyze large datasets (Chiu et al. 2001). It has the following desirable features that differentiate it from traditional cluster techniques: (1.) TSCA is able to analyze large datasets efficiently; (2.) TSCA is capable to automatically select the number of clusters; (3.) It has the ability to deal with both quantitative and qualitative variables. Because of these features, TSCA has been applied to different fields, such as biomedical studies (Babic et al. 2012), classification of synoptic systems (Michailidou et al. 2009), landslides deformation states identification (Wu et al. 2016), and so on to study pattern recognition.

As the name implies, the process has two steps termed “pre-clustering” and “clustering.”. In step one, the data are pre-clustered into many small sub-clusters based on a sequential cluster approach. In step two, the sub-clusters are used as inputs and clustered into the final number of clusters. To deal with both continuous and categorical variables, the log-likelihood function is used to derive the distance measurement in both steps. In calculating log-likelihood function, it is assumed that continuous variables are normally distributed, categorical variables are multinomial, and all variables are independent of each other.

Appendix 2. Determination of the relative weights of the conditional factors using BPNN

Assume the input vector, hidden vector, and output vector of the BPNN as X = (x₁, x₂, ..., x_i, ..., x_I), Y = (y₁, y₂, ...y_j, ..., y_J), and Z = (z₁, z₂, ..., z_k, ..., z_K), respectively. The expected output vector is labeled as O = (o₁, o₂, ..., o_k, ..., o_K). The expressions for the jth node in the hidden layer, y_j and the kth node in the output layer, z_k are respectively given below in Eqs. (9) and (10).

$$ {y}_j={f}_1\left({M}_j\right)={f}_1\left(\sum \limits_{i=1}^I{w}_{ij}{x}_i-{a}_j\right)\kern0.5em j=\left(1,2,...,J\right) $$

(9)

$$ {z}_k={f}_2\left({N}_k\right)={f}_2\left(\sum \limits_{j=1}^J{w}_{jk}{y}_j-{b}_k\right)\kern0.5em k=\left(1,2,...,K\right) $$

(10)

In Eq. (9), w_ij and a_j are the weights and thresholds respectively between the input layer and the hidden layer. Similarly, in Eq. (10), w_jk and b_k are the weights and thresholds between the hidden layer and the output layer. The main purpose of the BPNN is to adjust the weights and thresholds to minimize the mean square error (MSE) between the expected output values and network output values, as shown in Eq. (11).

$$ MSE=\frac{1}{K}\sum \limits_{k=1}^K{\left({o}_k-{z}_k\right)}^2 $$

(11)

The importance of node i with respect to node k is defined as ST_ik and is shown in Eq. (12). The overall importance of node i with respect to the output layer can be calculated as ST_i and is shown in Eq. (13).

$$ S{T}_{ik}=\frac{1}{J}\cdot \sum \limits_{j=1}^J{s}_{ij}\cdot {t}_{jk} $$

(12)

$$ S{T}_i=\frac{1}{J}\cdot \sum \limits_{j=1}^J{s}_{ij}\cdot {t}_j $$

(13)

In Eqs. (12) and (13), s_ij is the normalized importance of node i in the input layer with respect to node j in the hidden layer, t_jk is the normalized importance of node j in the hidden layer with respect to node k in the output layer, and t_j is the overall importance of node j, and they can be calculated by Eqs. (14), (15), and (16) as given below:

$$ {s}_{ij}=\frac{\mid {w}_{ij}\mid }{\mid {w}_{i_0j}\mid }=\frac{\mid {w}_{ij}\mid }{\frac{1}{I}\cdot \sum \limits_{i=1}^I\mid {w}_{ij}\mid }=\frac{I\cdot \mid {w}_{ij}\mid }{\sum \limits_{i=1}^I\mid {w}_{ij}\mid } $$

(14)

$$ {t}_{jk}=\frac{\mid {w}_{jk}\mid }{\mid {w}_{j_0k}\mid }=\frac{\mid {w}_{jk}\mid }{\frac{1}{J}\cdot \sum \limits_{j=1}^J\mid {w}_{jk}\mid }=\frac{J\cdot \mid {w}_{jk}\mid }{\sum \limits_{j=1}^J\mid {w}_{jk}\mid } $$

(15)

$$ {t}_j=\frac{1}{K}\cdot \sum \limits_{k=1}^K{t}_{jk} $$

(16)

Appendix 3. Rating calculation procedure

After data digitization and non-landslide set determination, the number of cells where landslides occurred and not occurred can be obtained along with the corresponding values for each factor. Then the rating of each class of every factor can be determined as the ratio of landslide occurrence (a_im) divided by the ratio of landslide non-occurrence (b_im), as expressed by Eq. (17).

$$ {R}_{im}=\frac{a_{im}}{b_{im}}=\left(\frac{l_{im}}{L}\right)/\left(\frac{n_{im}}{N}\right) $$

(17)

In Eq. (17), R_im is the rating of mth class of ith factor; l_im is the number of landslide cells falls in mth class of ith factor; n_im is the number of non-landslide cells falls in mth class of ith factor; L and N are respectively the total number of cells of landslide occurrence and non-landslide occurrence.

Appendix 4. Model validation

In the present study, for landslide susceptibility index model validation, firstly, a series of testing data consisting of LSI values that have been normalized to the range 0 to 1 are considered. Furthermore, these data should be categorized either under the existing landslide pixels, i.e., actual positive state, or under the non-landslide pixels, i.e., actual negative state. Secondly, a threshold level must be set to estimate the LSI values; above the level is called positive, i.e., landslide will occur, and below the level is called negative, i.e., landslide will not occur. Obviously, the setting threshold can affect the sensitivity and specificity (SPC). The sensitivity (TPR) is also called the proportion of true positive state. It can be calculated by Eq. (18) as the number of true positive pixels (TP) divided by the total number of actual positive pixels (P). The true positive state represents those pixels that are in the actual landslide area which get the positive test result, i.e. the red area in Fig. 8. The specificity (SPC) is the proportion of the actual non-landslide pixels that were identified correctly as negative, i.e. the blue area in Fig. 8. It can be calculated by Eq. (19). In Eq. (19), the false positive rate (FPR) can be calculated by Eq. (20) as the number of false positive pixels (FP) divided by the total number of actual negative pixels (N). The false positive state represents those pixels that are in the actual non-landslide area which get the positive test result, i.e. the marked area with diagonals to the right of 0.5 in Fig. 8. Therefore, when you set a series of thresholds to increase the sensitivity, it will lead to decrease of specificity, and vice versa. Thirdly, by varying the threshold values, a series of points having (TPR, FPR) values can be obtained. By connecting those points, the ROC curve and the area under the ROC curve can be obtained. The SPSS software was used to get the ROC curves and the AUC values.

$$ TPR=\frac{TP}{P}=\frac{TP}{TP+ FN} $$

(18)

$$ SPC=\frac{TN}{N}=1- FPR $$

(19)

$$ FPR=\frac{FP}{N}=\frac{FP}{TN+ FP} $$

(20)

Fig. 8

Schematic diagram of the ROC curve