Introduction

The term landslide refers to a specific type of geological hazard characterized by the downslope movement of rock, soil, or related debris. Landslides have the potential not only to cause massive casualties and property losses but also to pose a great risk to natural resources, the environment and ecology in general. The deformation process of a landslide is a complex, multi-dimensional, nonlinear dynamic system that is affected by complex geological conditions and diverse triggering factors (Cao et al. 2016). Landslide displacement is the result of the combined effects of internal geological conditions and external triggering factors and, consequently, there is a large element of uncertainty (Federico et al. 2012; Miao et al. 2017). Research on landslide displacement prediction, with a focus on effectively reducing the risk of a landslide failure and providing adequate countermeasures for landslide control, is a challenging issue worldwide.

With the rapid development of artificial intelligence and machine learning, a large number of data mining methods and nonlinear intelligent integrated systems have been proposed. Several representative approaches have been successfully applied to landslide displacement prediction (Alimohammadlou et al. 2014; Newcomen and Dick 2016). The artificial neural network (ANN), support vector machine (SVM) and extreme learning machine (ELM) are three typical approaches for predicting the landslide displacement (Gao and Jiang 2012; Du et al. 2013; Pradhan 2013; Cao et al. 2016; Miao et al. 2017). Although the above intelligent algorithms have achieved excellent performance, there are still several limitations to their use. For example, the ANN (such as a back propagation [BP] neural network) must set training parameters, such as the number of hidden layers and the number of nodes in each layer, when it is initialized, which leads to the occurrence of local optimal solutions (Kumar et al. 2017). The SVM has been extensively used in data forecasting since it has often been found to outperform ANN (Miao et al. 2017), but the model has difficulties in selecting parameters that have to be tuned for optimal regression performance. The ELM is a new algorithm that has been proposed in recent years (Huang et al. 2006). Based on the single-hidden layer feedforward neural network (SLFN), the ELM solves the difficult problem of determining the number of hidden layers in the neural network (Huang et al. 2017). Compared with the previous prediction models, such as the BP neural network and SVM, the ELM has a faster learning speed and a better generalization ability (Lian et al. 2013). However, the results are not sufficiently stable since the ELM inputs the weight matrix through a random mapping step.

To solve the problem of unstable results of an ELM, Huang et al. (2012) proposed a kernel extreme learning machine (KELM). The KELM can greatly improve the accuracy of prediction of an ELM by optimizing the model parameters; in traditional methods, these parameters are mainly processed by the grid search method and the gradient descent method. In addition, metaheuristic search algorithms, such as the particle swarm optimization (PSO) and genetic algorithm (GA), can also be applied to optimize the parameters (Cai et al. 2016; Zhou et al. 2016). The grey wolf optimizer (GWO), a new population-based metaheuristic algorithm that imitates the hunting behavior of wolves, has the advantages of simple principles, few parameters and a strong global search ability (Mirjalili et al. 2014). Compared with the some of the other algorithms (e.g. particle swarm optimization [PSO] algorithm and genetic algorithm [GA]), the GWO has been proven to be suitable for combinatorial optimization problems and is widely applied in various applications for feature selection, template matching, economic dispatch, among others (Song et al. 2015; Sulaiman et al. 2015; Emary et al. 2016; Jayabarathi et al. 2016; Zhang and Zhou 2017).

We report here a case study on the Baishuihe landslide, a typical step-like landslide in the Three Gorges Reservoir Area (TGRA) of China. Based on the time series principle, we divide the cumulative displacement of the Baishuihe landslide into trend displacement and periodic displacement. The moving average method is used to extract the trend displacement that can be predicted by the cubic polynomial function. In addition, the GWO algorithm is introduced into the KELM model so that a GWO-KELM model is established to predict the periodic displacement. The prediction results are then analyzed according to three evaluation criteria: the root mean square error (RMSE), mean absolute percentage error (MAPE) and goodness of fit (R2). Based on these results, we propose a new method to predict the displacements of step-like landslides in the TGRA.

Methodology

Time series theory

Landslide displacement is a non-stationary time series that changes over time (Ren et al. 2015; Ma et al. 2017a, b). Considerable research in the TGRA of China has revealed that the cumulative displacement of landslide in this area is caused by the combined effects of internal geological conditions (lithology, geological structure, topography, etc.), external environmental factors (rainfall, reservoir water level, etc.) and random factors (uncertainties) (Lian et al. 2015; Zhou et al. 2016; Wen et al. 2017). Landslide displacement due to internal geological conditions shows a monotonically increasing function over time, which may be referred to as trend displacement. Displacement under the influence of external environmental factors shows an almost periodic function over time, which may be referred to as periodic displacement. Therefore, based on this distinction, the cumulative displacement time series can be decomposed as follows:

$$ X(t)=\varphi (t)+\eta (t)+\delta (t) $$
(1)

where t is time, X(t) is the time series displacement, φ(t) is the trend displacement, η(t) is the periodic displacement and δ(t) is the random displacement.

The random displacement is mainly influenced by random factors (wind load, vehicle load, vibration load, etc.). However, as the influence of these factors is relatively limited and difficult to determine, we have not considered random displacement in this study. Equation (1) can be simplified to:

$$ X(t)=\varphi (t)+\eta (t) $$
(2)

Kernel extreme learning machine model

The KELM is an improved model that combines an ELM with a kernel function (Zhou et al. 2018). The ELM adopts the SLFN training method (Huang et al. 2006), which can calculate the output weight of the network with a one-step computation. Therefore, the ELM has a fast learning speed. When the training sample is D = {(xn, yn), n = 1, 2…N}, the regression function is defined as follows:

$$ \hat{y}=f(x)=h(x)\beta = H\beta $$
(3)

where x is the input vector, \( \hat{y}=f(x) \) is the network output, h(x) = H is the random feature mapping matrix of the hidden layer and β is the link between the weight of the hidden layer and the output layer.

According to the generalized inverse matrix theory, β can be expressed as:

$$ \beta ={H}^{\mathrm{T}}{\left(I/C+{HH}^{\mathrm{T}}\right)}^{-1}y $$
(4)

where I is the diagonal matrix, C is the penalty coefficient, y is the output target vector and y = [y1, y2, …, yn]T, n = 1, 2…N.

Huang et al. (2014) proposed the KELM model that incorporates a kernel function into the ELM to replace the random mapping in ELM. The operational structure of the KELM is shown in Fig. 1 (Shamshirband et al. 2015).

Fig. 1
figure 1

Structure of the kernel extreme learning machine (KELM) regression

Full size image

The KELM kernel matrix is defined as follows:

$$ \left\{\begin{array}{l}{\Omega}_{\mathrm{ELM}}={HH}^{\mathrm{T}}\\ {}{\Omega}_{\mathrm{ELM}i,j}=h\left({x}_i\right)h\left({x}_j\right)=K\left({x}_i,{x}_j\right)\end{array}\right. $$
(5)

where K(xi, xj) is the kernel function. The kernel function is usually set as a radial basis kernel (RBF function) (Zhou et al. 2016).

$$ K\left({x}_i,{x}_j\right)=\exp \left(-\gamma {\left\Vert {x}_i-{x}_j\right\Vert}^2\right),\gamma >0 $$
(6)

The output weight of the KELM obtained from Fig. 1 and Eqs. (4)–(6) is as follows:

$$ \hat{y}=f(x)={\left[\begin{array}{l}K\left(x,{x}_1\right)\\ {}K\left(x,{x}_N\right)\end{array}\right]}^{\mathrm{T}}{\left(I/C+{\Omega}_{\mathrm{ELM}}\right)}^{-1}y $$
(7)

The KELM uses the kernel function to map samples from the input space to the featured space with a high-dimensional hidden layer. Therefore, the KELM replaces the random mapping of the ELM with a stable kernel mapping, a substitution which enhances the stability and generalization ability of the model. The kernel function directly uses the inner product form, so the KELM does not need to set the number of hidden layers.

The parameters γ and C have a great influence on the KELM, where γ is a parameter that comes with the function after RBF has been selected as the kernel function. The kernel function parameter γ defines the impact of a single training sample and implicitly determines the distribution of the data mapped to the new feature space. C is the penalty coefficient, which is the tolerance of the relative error. Better results can be obtained by choosing appropriate values for the γ and C parameters. Therefore, the GWO algorithm is introduced to optimize the γ and C values and improve the performance of the model.

Grey wolf optimizer algorithm

The GWO algorithm is a new swarm intelligence optimization algorithm that was proposed by Mirjalili et al. (2014). It is derived from simulating the hunting behavior of grey wolves, and the algorithm achieves the goal of optimization through tracking, enveloping and attacking the prey.

Definition 1: Social hierarchy

The grey wolves maintain orderly social hierarchy during the hunting process. According to the level of the social hierarchy, the GWO algorithm can be equivalently divided into alpha (α), beta (β), delta (δ) and omega (ω) wolves. In the algorithm, the social hierarchy indicates the fitness level.

Definition 2: Surrounding the prey

The wolves usually surround the prey and determine the position of the prey during the predation. The positions of the grey wolves are considered to be variables in the hunting process, and the distances between the prey and the grey wolves determine the fitness value of the objective function. Mirjalili et al. (2014) gave the mathematical equation of the encirclement behavior as follows:

$$ \overrightarrow{\boldsymbol{D}}=\left|\overrightarrow{\boldsymbol{C}}\cdot \overrightarrow{{\boldsymbol{X}}_p}(w)-\overrightarrow{\boldsymbol{X}}(w)\right| $$
(8)
$$ \overrightarrow{X}\left(\boldsymbol{w}+1\right)=\overrightarrow{X_p}\left(\boldsymbol{w}\right)-\overrightarrow{\boldsymbol{\mu}}\cdot \overrightarrow{D} $$
(9)

where \( \overrightarrow{\boldsymbol{D}} \) defines the distance between a grey wolf and the prey, w is the current number of iterations, \( \overrightarrow{{\boldsymbol{X}}_p}(w) \) is the position vector of the prey, \( \overrightarrow{\boldsymbol{X}}(w) \) is the position vector of a grey wolf, \( \overrightarrow{\boldsymbol{C}} \) is a coefficient vector and \( \overrightarrow{\mu} \) is a convergence vector.

The vectors \( \overrightarrow{\boldsymbol{C}} \) and \( \overrightarrow{\mu} \) can be calculated as follows:

$$ \overrightarrow{\boldsymbol{C}}=2\cdot \overrightarrow{r_1} $$
(10)
$$ \overrightarrow{\mu}=2\overrightarrow{a}\cdot {\overrightarrow{r}}_2-\overrightarrow{a} $$
(11)

where \( \overrightarrow{r_1} \), \( \overrightarrow{r_2} \) are random vectors in [0,1], and \( \overrightarrow{a} \) decreases linearly from 2 to 0 during the iteration process. This means that \( \overrightarrow{\mu} \) is a random value in the interval [−a,a]; when random values of \( \overrightarrow{\mu} \) are in [−1, 1], the next position of a search agent can be in any position between its current position and the position of the prey. That is, |\( \overrightarrow{\mu} \)| ≥ 1 forces the grey wolves to diverge from the prey to hopefully find a fitter  prey.

Definition 3: hunting the prey

The predation process of the wolves is represented by the continuous updating of the hunting position information. In the iterative process, the algorithm saves the current position of the best three wolves (α, β, δ), and updates the position information of the other wolves (ω) to obtain the optimal solution. The final position will be in the circle defined by the search areas of α, β and δ. The hunting behavior can be expressed as Eqs. (12), (13) and (14), respectively:

$$ {\overrightarrow{\boldsymbol{D}}}_k=\left|{\overrightarrow{\boldsymbol{C}}}_i\cdot \overrightarrow{{\boldsymbol{X}}_k}(w)-\overrightarrow{\boldsymbol{X}}(w)\right| $$
(12)
$$ {\overrightarrow{X}}_i=\overrightarrow{X_k}-\overrightarrow{\mu_i}\cdot \overrightarrow{D_k} $$
(13)
$$ \overrightarrow{X_p}\left(\boldsymbol{w}+1\right)=\frac{\overrightarrow{X_1}+\overrightarrow{X_2}+\overrightarrow{X_3}}{3} $$
(14)

where the parameters k = α, β, δ and i = 1, 2, 3.

GWO-KELM prediction model

According to the above introduction to the GWO-KELM prediction model, the parameters γ and C have a great influence on the KELM. Therefore, in our study we encode the parameters γ and C as variables optimized by the GWO, corresponding to the two dimensions of the wolf positions in the algorithm (Wang et al. 2017; Dai et al. 2018). In addition, the fitness function is evaluated based on the training set using a KELM that is integrated with the GWO algorithm, and guided by the RMSE (Eq. (15)). For the minimization optimization problem, the smaller the value of the objective function corresponding to the search individual, the larger the fitness value (Liu et al. 2019). The detailed optimization process is as follows.

  1. Step 1:

    Initialize the ranges of values of γ and C in the KELM and set the relevant parameters in the GWO algorithm.

  2. Step 2:

    Randomly generate the wolf population and make the position vector of each wolf based on C and γ.

  3. Step 3:

    The KELM learns the training set based on the initial γ and C values and calculates the fitness value of each grey wolf. The wolf with the best fitness value is α, the wolf with the second best fitness value is β, the wolf with the third best fitness value is δ, and the remaining wolves are ω.

  4. Step 4:

    According to Eqs. (12)–(14), the distance and moving direction between individual wolves and α, β, δ are updated, and the position of each wolf is updated according to Eqs. (8)–(11).

  5. Step 5:

    Update the positions of the wolves to generate a new population, calculate the corresponding

    fitness values and compare these values with those of the last iteration to retain the preferred wolves.

  6. Step 6:

    When the maximum number of iterations is reached, end the training and output the optimized γ and C values. Otherwise, turn to Step 4 to continue the optimization of parameters.

  7. Step 7:

    The optimal parameters γ and C are used to establish the KELM prediction model, and the prediction results are analyzed.

Hybrid model and performance evaluation

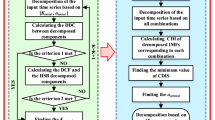
In the study reported here, the trend displacement and the periodic displacement are separated by time series decomposition. The cubic polynomial function method is used to fit and predict the trend displacement. The GWO algorithm is introduced into the KELM model, so the periodic displacement is trained and predicted. A KELM model with GWO is proposed and named the GWO-KELM model. The basic flow of the prediction process is shown in Fig. 2.

Fig. 2
figure 2

Analytical flowchart of the prediction process

Full size image

To assess the prediction performance of the model, we used three statistical indices, namely, the RMSE, MAPE and R2 (Cai et al. 2016; Zhou et al. 2018). The RMSE is a frequently used measure of the differences between the values predicted by a model or an estimator and the actual values observed, and it represents the square root of the second sample moment of the differences between the predicted values and observed values or the quadratic mean of these differences (Eq. (15)). The MAPE is the average absolute percentage error for each time period or forecast minus the actual values divided by actual values (Eq. (16)). Without considering the direction of the error, the smaller the RMSE and MAPE are, the better the prediction effect of the model is. The R2 value of a statistical model describes how well it fits a set of observations. The calculated value of R2 typically reflects the discrepancy between the observed values and expected values under the model in question. The larger the value of R2 is, the better the fitting effect is.

The formulas of the three indices are shown as follows:

$$ RMSE=\sqrt{\frac{1}{N}\sum \limits_{i=1}^N{\left({\hat{X}}_i-{X}_i\right)}^2} $$
(15)
$$ MAPE=\frac{1}{N}\sum \limits_{i=1}^N\left|\frac{{\hat{X}}_i-{X}_i}{X_i}\right| $$
(16)
$$ {R}^2=1-\frac{N\sum {\left({X}_i-{\hat{X}}_i\right)}^2}{N\sum {X_i}^2-\sum {{\hat{X}}_i}^2} $$
(17)

where N is the number of the cumulative displacements; Xi represents the observed cumulative displacements; and \( {\hat{X}}_i \) represents the predicted cumulative displacements.

Case study: Baishuihe landslide

Geological conditions

The Baishuihe landslide is located in Zigui County, on the right bank of the Yangtze River, 56 km from the Three Gorges Dam (Miao et al. 2017). The landslide is a typical example of a loose deposit landslide in the TGRA. The main sliding direction is 20° NE, and on the side facing the Yangtze River, the landslide is fan-shaped in a plane with a maximum length of 780 m and maximum width of 700 m. The bedrock of the Baishuihe landslide is composed of sandstones silty mudstone and sand muddy siltstones of the Jurassic Xiangxi Formation, and the overall slope angle is approximately 30° (Lu et al. 2014). The materials on the surface of the landslide bedrock are mainly composed of Quaternary deposits with silty clay and fragmented rubble (Huang et al. 2017). The sliding mass has an average depth of approximately 30 m, and its volume is approximately 1.26 × 107m3 (Liu et al. 2014). The topographical map and the schematic geologic cross-section are shown in Fig. 3a and b, respectively.

Fig. 3
figure 3

a GPS monitoring displacements of the Baishuihe landslide by GPS, b schematic geologic cross-section of the Baishuihe landslide

Full size image

Monitoring of the Baishuihe landslide began in June 2003 when the reservoir water level was 135 m. The layout of the GPS monitoring points (Li et al. 2010; Liu et al. 2016) is shown in Fig. 3a. The Baishuihe landslide is divided into three regions, namely A, B and C, according to the characteristics and monitoring data of the surficial deformation. The warning areas of A and C are located at the mid-front part of the intensely deformed landslide where the cumulative displacement is enormous and the deformation occurs in a step-like manner. Located on the east side of the warning areas are numerous transverse tensile cracks that appear to be feathered; to the westthere are many secondary landslides and tiny cracks. The B region is located at the back of the Baishuihe Landslide and is characterized by a slow rate and a small amount of deformation, such that this area is almost stable.

Deformation characteristic analysis

As shown in Fig. 3a, 11 GPS monitoring locations are present on the Baishuihe landslide. We have selected the GPS information from monitoring location ZG93 to establish the forecasting model because GPS data from this location effectively describes the entire process of the landslide movements; consequently these monitoring data are representative and can show the deformation of the entire landslide. Figure 4 shows the evolution of the landslide categorized into three phases, i.e. phases I, II and III (Du et al. 2013; Yang et al. 2019) according to the scheduling dates of the water level in the reservoir and the monitoring displacement information from GPS monitor ZG93 from June 2003 to November 2011 (Zhang et al. 2014), :

Fig. 4
figure 4

Cumulative monitoring displacement, daily rainfall and reservoir water level over the period June 2003 to November 2011. ZG93 Location of GPS monitor used as source of data for the study

Full size image

Phase I (June 2003–September 2006)

Based on the periodic scheduling data of the reservoir water level, the reservoir began to fill in September of each year. The displacement of the monitoring point underwent only minor changes with increasing water level in the reservoir, indicating that the effect of increasing reservoir water levels on the displacement was weak. The reservoir water level began to drop in February of each year, and the corresponding displacement of the monitoring point increased after 1–2 months due to the “lag effect.” The main reason for the “lag effect” is that the response of the internal water level in the landslide lagged behind the scheduling of the reservoir water level. Therefore, when the reservoir water level rose, it had little effect on the displacement; and when the reservoir water level dropped, the displacement increased only slightly. However, as shown in Fig. 4, the displacement continued to increase throughout the entire phase. Combined with the data of seasonal rainfall data during the period (mainly from June to September each year), we believe that the main cause of the continuous increase of the displacement was rainfall and that the influence of reservoir water level on the displacement was relatively small.

Phase II (September 2006–September 2008)

From September to November 2006, the reservoir water level increased from 135 to 155 m within a short time, and the displacement of the landslide remained stable for a long time, which reinforced the notion that increasing reservoir water level had little effect on landslide displacement. After February 2007, the level of water in the reservoir water fell to 145 m for the first time. During this period, the landslide experienced continuous rainfall, and the largest step-like deformation was observed. The cumulative deformation reached 828 mm, and the drawdown of reservoir water level and seasonal rainfall were considered to be the causal factors. In phase II, there were two periodic scheduling of reservoir water drawdown during the seasonal rainfall. When the reservoir water level dropped markedly for the second time, a step-like deformation was also produced in the landslide, but the amplitude of this step-like deformation was significantly lower than that of the first decrease in water level because due to the seepage field, the stress field and the structure of the sliding soil in front of the landslide had undergone a large adjustment and, therefore, the impact of the drawdown of reservoir water level on the displacement had gradually weakened. According to the phase II analysis, the drawdown of the reservoir water level was the main controlling factor for the step-like deformation.

Phase III (September 2008–November 2011)

During this period, the reservoir water level rose from 145 to 175 m, and the displacement did not change substantially. When the reservoir water level dropped sharply from 175 to 145 m for the first time, there was no substantial deformation based on data from the monitoring point, but there was a weak step-like movement, which showed that the impact of the declining water levels on the landslide displacement tended to be stable. In the subsequent scheduling of the reservoir water level and seasonal rainfall, the displacement of the monitoring point continued to decrease and the step-like characteristic continued to weaken. This finding indicates that the displacement produced during this period was the result of the combined effects of the reservoir water and seasonal rainfall.

Calculations and results

In this study, displacement at the ZG93 monitoring site during phase III was selected as the research object because the response of the landslide system to the fluctuation in reservoir water had gradually stabilized in this phase. Both reservoir water level and seasonal rainfall usually decline between June and September each year (Liu et al. 2016; Ma et al. 2018), taking into account the “lag effect,” so the training samples and the test samples were selected during this period. The cumulative displacement series from December 2008 to May 2011 were selected as the training samples, and the cumulative displacement series from June 2011 to November 2011 were selected as the test samples.

Displacement decomposition

According to the principle of the time series, the cumulative displacement can be decomposed into trend displacement and periodic displacement. The trend displacement of a landslide is controlled by geological conditions, representing the main trend of landslide deformation. The trend displacement is extracted by the moving average method (Eq. (18)).

The displacement extracted by the moving average method can smooth the short-term fluctuations and reflect the long-term trends. The method assumes that the displacement monitoring value at time t is x(t) and that the trend displacement at time t is φ(t); therefore, the calculation formula is:

$$ \varphi (t)=\frac{x(t)+x\left(t-1\right)+\dots +x\left(t-k+1\right)}{n},\left(t=k,k+1,\dots, n\right) $$
(18)

where x(t − k + 1) is the value of the displacement monitoring at the time t − k + 1, and n is the moving average periodic.

In view of scheduling of the reservoir water in the TGRA, the moving average period (n) is set as 12, which means 12 months of the year. Figure 5a shows the extracted results from the monitoring displacement of the Baishuihe landslide.

Fig. 5
figure 5

Extraction values of trend displacement (a) and periodic displacement (b)

Full size image

Based on the time series principle, the periodic displacement η(t) is obtained by removing the trend displacement (φ(t)) from the cumulative displacement (X(t)). Figure 5b shows the extracted periodic displacement.

In view of the fitting accuracy and the Runge phenomenon in the function, we adopted a cubic polynomial method (Eq. (19)) to fit the trend displacement on the time axis (Yang et al. 2014; Zhou et al. 2016). The results and accuracies of this cubic polynomial method are shown in Table 1.

$$ \varphi {(t)}^{\prime }={at}^3+{bt}^2+ ct+d $$
(19)
Table 1 The parameters of trend displacement based on polynomial fitting
Full size table

Impact factors of periodic displacement

The prediction of periodic displacement is a key to predicting landslide displacement and directly affects the precision of the prediction. Therefore, it is crucial to correctly select the factors impacting the periodic displacement. According to the above analysis of the Baishuihe landslide, the reservoir water level and rainfall are the main controlling factors that can effectively affect the periodic displacement (Li et al. 2010).

Rainfall is one of the most important external environmental factors, frequently triggering landslides in the TGRA (Liu et al. 2016; Xu and Niu 2018). On the one hand, rainfall infiltration leads to the physical reaction of sliding soil, which may promote the formation of saturated sliding soil and produce dynamic pressures. At the same time, because the Baishuihe landslide is a typical loose deposit landslide, the rainfall infiltration can easily form a water channel, penetrate the damaged surface and subsequently reduce the stability of the slope. On the other hand, rainfall causes a water–soil chemical reaction that promotes the combination of hydrophilic substances and water to make the sliding soil muddy, softened, and disintegrated (Alimohammadlou et al. 2014; Xu et al. 2016). The influence of rainfall on landslide deformation is a continuous but slow process, which is mainly controlled by the intensity and duration of the rainfall (Keefer et al. 1987; Ali et al. 2014). Therefore, the 1- and 2-month preceding precipitation were selected as the factors (Bernardie et al. 2015) that affect the periodic displacement (Fig. 6a).

Fig. 6
figure 6

a–c Relationship between rainfall and period displacement (a), between change in reservoir water level and periodic displacement (b) and between monthly displacement change and periodic displacement (c)

Full size image

The periodic scheduling of the reservoir water level is the main factor that contributes to the step-like characteristic of the landslides in the TGRA (Jiao et al. 2014) (Fig. 6b). Fluctuations in the reservoir water level have not only a strength softening effect of on sliding soil, leading to a decrease in the shear strength of the soil (Yao et al. 2015), but they also affect the distribution of the groundwater dynamics and change the seepage field (Tang et al. 2015; Ma et al. 2018). The impact of the reservoir water level on landslide displacement is usually a slow process. We took the “delay effect” in the Baishuihe landslide into account and selected the reservoir water level and the 1- and 2-month variations in reservoir water level selected as the factors that affect the periodic displacement.

Under the combined effects of the reservoir water level and rainfall, the periodic displacement time curve of the landslide presents a periodic characteristic. It can be seen from Fig. 6c that the change inmonthly displacement and the periodic displacement show a certain correlation. During the periods of variations in reservoir water level and rainfall, the periodic displacement shows a positive, regular correlation with time: when the periodic displacement increases, the change in monthly displacement increases concomitantly. When the periodic displacement is gradually weakened after variations in reservoir water level and rainfall, accordingly, the monthly displacement change fluctuates slightly. Therefore, the change in monthly displacement can be used as a supplement to characterize the influence of other cyclic factors that are not considered adequate to characterize the landslide displacement.

Consequently, data on six factors that influence the periodic displacement are obtained. According to grey relational analysis (Gau et al. 2006), when the resolution coefficient is taken as 0.5 and the correlation degree (rk) between the impact factors and periodic displacement is > 0.6, impact factors and the periodic displacement can be considered to be closely related. As shown in Table 2, the correlation degree of the six impact factors is > 0.6, which verifies the rationality of our selection of parameters.

Table 2 Grey relational degree between the impact factors and periodic displacement
Full size table

Parameter setting in the models

The GWO-KELM model is used to predict the periodic displacement of the landslide. Meanwhile, the ELM with GWO (GWO-ELM), the SVM with GWO (GWO-SVM) and ELM models are used in the comparison experiments. The prediction process is detailed as follows:

  1. (1)

    Data preprocessing. To eliminate the influence of the data dimension, the impact factors and periodic displacement are normalized to different intervals [0, l].

  2. (2)

    Parameter initialization. The impact factors are used as the input vectors, and the periodic displacement is used as the output vector to establish the relationship between the impact factors and periodic displacement. The parameter initialization settings of the four models are shown in Table 3 (Song et al. 2015; Dai et al. 2018).

    Table 3 The parameter initialization settings of the four models
    Full size table
  1. (3)

    Optimal parameters. The GWO algorithm is applied to search the global optimal parameters of the learning machine model. The GWO-KELM and GWO-SVM use the kernel function mapping to obtain stable parameters by optimizing γ and C. The search range of parameters γ and C is [0.01, 100] (Wang et al. 2017), and the results of the optimization are [99.96, 83.283] and [0.25, 4.87], respectively. However, in the comparison experiments, the random method is used for the mapping from the input space to the featured space in the GWO-ELM and ELM models, so the optimization results are unstable and the parameters vary greatly.

  1. (4)

    Prediction results.The prediction model, which can be used to forecast the periodic displacement, is established by using the optimized parameters. Figure 7 and Table 4 show the results of prediction accuracy for each model.

    Table 4 Accuracy assessment of different forecasting models
    Full size table
Fig. 7
figure 7

Prediction and comparison of (a) periodic displacement and (b) measured total displacement. Models: GWO-KELM Kernel extreme learning machine with grey wolf optimization (GWO), GWO-ELM extreme learning machine with GWO, GWO-SVM kernel extreme learning machine with GWO, ELM extreme learning machine

Full size image

Results and analysis

As shown in Fig. 7a and Table 4, the predictions of the GWO-KELM and GWO-ELM methods are clearly better than those of the GWO-SVM and original ELM methods.

The ELM contains a large number of variable parameters, which make the results unstable. When GWO is introduced into the ELM, the advantages of GWO (few parameters to set and strong global search ability) can be exploited. Therefore, the GWO-ELM model can determine the optimal parameters for better and more stable prediction. Our comparison of the GWO-ELM and the original ELM revealed that the GWO-ELM shows a significant improvement in terms of forecasting through optimization of the parameters.

Both the GWO-ELM and GWO-SVM use the same optimization method to control the initial values of the parameters, but the prediction results vary greatly between the two models. This variation is mainly due to the difference in the learning mechanism between the ELM and SVM. In our comparison experiment, the penalty factors and kernel function parameters of the GWO-SVM are mainly optimized. However, the influence range of the parameters is limited and the generalization ability is weak in the GWO-SVM and, consequently, the prediction effect is poor.

Both the GWO-KELM and GWO-ELM use GWO as the optimization algorithm for the respective model. The difference between the two models is that the GWO-KELM model adopts the kernel function to map the samples from the input space to the featured space and replaces the random mapping in GWO-ELM with a more stable kernel mapping.

The cumulative displacement of the landslide can be obtained by superposing the trend displacement and the periodic displacement, as shown in Fig. 7b.

The GWO-KELM model enhances the stability and generalization ability of the model. Moreover, the GWO-KELM model noticeable improves the efficiency of the global search and avoids the inherent drawbacks of models using GWO. At the same time, the KELM fully integrates the advantages of the ELM with the kernel function. The RMSE, MAPE and R2 of the GWO-KELM model are 7.75, 0.31%, and 0.8239, respectively, in predicting the cumulative displacement of the Baishuihe landslide.

Discussion

Periodic factors, such as seasonal rainfall and reservoir water level, were found to control the step-like deformation behavior of the Baishuihe landslide in the TGRA. Four machine learning models were implemented to predict the step-like displacement of the landslide. The SVM and ELM are two representative machine learning methods that are used to predict landslide displacement by optimizing the parameters. Thus, the proposed model (GWO-KELM) was compared with the GWO-SVM, GWO-ELM and ELM models. The proposed model introduced a kernel function to the ELM and was first implemented in an optimized KELM model with GWO. The GWO-KELM solved the problem of the unstable results produced by the GWO-ELM and ELM. In addition, the GWO-KELM demonstrated better prediction precision and generalization ability than the GWO-SVM and was effective for predicting the landslide with a step-like behavior.

Although the proposed model yields better results than the other three approaches, there are still some problems that have not been adequately addressed. For example, a sudden change in the trigger factors and the selection of the impact factors in the real world are not considered comprehensively in the proposed model. Moreover, due to the limitations of existing monitoring data, it remains difficult to predict the landslide displacement over long periods. The landslide displacement is a non-stationary time series that changes over time. Therefore, the latest monitoring data should gradually be substituted, while the earlier information should be removed to achieve a better prediction.

Conclusions

The Baishuihe landslide in the TGRA has a typical step-like deformation characteristic due to the unique geological conditions in the area and external environmental factors. We have considered the influence of the geological conditions (lithology, geological structure, topography, geomorphology, etc.) and environmental factors (rainfall, reservoir water level, etc.) on the Baishuihe landslide and decomposed the cumulative displacement of this landslide with a step-like behavior. Based on time series, the cumulative displacement is divided into the trend displacement and the periodic displacement, with the latter having a clear physical and mathematical meaning.

A clear step-like deformation of the landslide occurred following the distinct drop in the reservoir water level; this deformation was the result of various factors (physical, chemistry and geological conditions) of the landslide. The effects of such factors tend to be stable over time, and the combined effects of rainfall and reservoir water level are the primary reasons for the cumulative deformation in the subsequent stage.

The periodic displacement can be predicted by the selected impact factors. The results of periodic displacement prediction show that the GWO-KELM model performs better than the GWO-ELM, GWO-SVM and ELM models in the case of the Baishuihe landslide. Compared to the other models, the GWO-KELM model has a better generalization ability and reduces the interference of human factors in the modeling process. The periodic displacement obtained by the GWO-KELM model is superimposed with the trend displacement to obtain the total displacement of the landslide, and a good prediction precision is obtained. Therefore, this hybrid method has the potential for broad application to predict the other landslides with a step-like deformation characteristic in the TGRA.